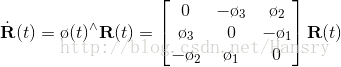SLAM学习——李群与李代数

1.李群与李代数基础

三维旋转矩阵构成特殊正交群SO（3），而变换矩阵构成了特殊欧氏群SE（3）：

其中特殊正交群SO(3)和特殊欧氏群SE(3),对加法不封闭，而对乘法封闭。则有：

群，是一种集合加上一种运算的代数结构，主要满足有：封闭性、结合律、幺元、逆等性质。而李群，则是指具有连续光滑性质的群。

对于李代数，考虑任意旋转矩阵 R,会随着时间变化而变化，即为时间的函数：R(t)。
则有：

通过对其时间的求导，可得到一个等式：

其中 为反对称矩阵，对于反对称矩阵而言，我们总能找到一个向量与之对应，对以上的反对称矩阵，我们记这个向量为 ,则有：

由于 R 为正交矩阵，则有

我们可以看到，每对旋转矩阵求一次导，只需左乘一个上述矩阵即可，设 to=0，且R(0)=I,通过一阶泰勒展开解上述微分方程，可以得到：

该方程说明了旋转矩阵R通过一个反对称矩阵通过指数关系发生了联系。

对于李代数而言，在不引起歧义的情况下，我们可以说李代数的元素是上述所提到的向量和反对称矩阵，而李代数so(3),（注意这里与SO(3)不同），则元素为三维向量和三维反对称矩阵，而se(3)的元素是六维向量和六维反对称矩阵，其表达方式为：

对于se(3)里面的p的三维向量，代表的是平移，但是含义与变换矩阵中的平移是不同的，这点需要特别注意，另外在se(3)李代数中，符号“ ^“仅仅表示向量到反对称矩阵，而是广泛的表达为从”向量到矩阵“。

2.指数与对数映射

上面我们提到了,它是一个矩阵的指数，在李群和李代数中，称为指数映射。通过一系列的泰勒展开计算，我们可以得到:

其中， 代表三维向量的模长，而a代表长度为1的方向向量。通过上述公式可得，so(3)实际上就是所谓的旋转向量。通过这种指数映射，意味着SO(3)中的元素，都可以找到一个so(3)的元素与之对应，但是可能存在多个so(3)对应到同一个SO(3)，毕竟so(3)在一定程度上就是由旋转向量组成的空间。如果把旋转角度固定在 中，那么李群和李代数就是一一对应的了。

3.李代数求导与扰动模型

为什么要使用李代数呢？使用李代数的一大动机是用来进行优化，因为在从空间点到观测数据的转换时，总会有噪音的存在，优化机器人的位姿使得噪声最小。

对某个旋转矩阵R，对应的李代数为 ，当左乘一个微小的旋转 后，对应的李代数为 。那么在李群上我们得到的结果是 ,而在李代数上，根据BCH近似，我们得到的结果是 ，由此可以得到公式为：

而对于se(3)李代数而言，同样有类似的性质。

对于李代数求导问题，在SLAM中，我们要估计一个相机的位姿，该姿态是由李群上的SO(3)和SE(3)而来的。那么，假设某时刻摄像机的位姿为T,观察到了点 p，得到了观测数据z，那么有： z=Tp+w，其中w为观测误差。

为了使得实际值与观测值最大程度的接近，那么我们需要使噪声最小，而这个即是优化的过程，通过对转换矩阵 T 的求导，得到整体误差的最小化：

为了求解这个问题，我们经常会构建与位姿有关的函数，然后讨论该函数关于位姿的导数，以调整当前的估计值。因为变换矩阵只是单纯的李群，对加法不封闭，于是我们可以转换成李代数进行求导。因为李代数由向量组成，所以具有良好的加法运算。在求解李代数问题时，有俩种思路：

1.用李代数表示姿态，然后根据李代数加法来对李代数求导
2.对李群左乘或者右乘一个微小扰动，然后对该扰动求导，称为左扰动模型和右扰动模型。第一种对应到李代数的求导模型，第二种对应到扰动模型。

李代数求导模型

关于李代数求导，考虑到SO(3)，假设对一个空间点 p 进行了旋转，得到了 Rp ，要计算旋转后点的坐标相对于旋转的导数，有：,但是对于李群而言对加法不封闭，所以该导数无法按照导数的定义进行计算。设 R 对应的李代数为 ，那么转而计算有：。

于是，按照导数的定义，我们可以有：**=(雅克比矩阵)（其中推导省略），但是由于在这里我们需要计算雅克比矩阵，所以过程比较复杂，转而学习下面的扰动模型。

扰动模型（左乘）

在模型之前，有麦克劳林展开式有：

y=e^x运用麦克劳林展开式并舍弃余项：e^x≈1+x+x^2/2!+x^3/3!+……+x^n/n!

接着上述问题，另一种求导方式为，对R进行一次扰动 ，设左扰动对应的李代数为 ，对其进行求导有：

该式求导比上述简单：

最终得到结果省去了计算一个雅克比矩阵，这使扰动模型更加有用！！其中，第二步到第三步运用了麦克劳林展开式，舍去了高次项。从第四步到第五步，可以将反对称符号看做叉积，变换之后变号，从而求得结果！！

最后，这些模型的求解可以一个Sophus库进行协助求解！！！