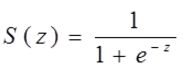MATLAB之线性回归,逻辑回归,最小二乘法,梯度下降,贝叶斯,最大似然估计
文章目录
- 线性回归(定义域(-∞,+∞),值域(-∞,+∞),即输入输出连续)
- 线性回归/最小平方误差理论
- MATLAB之线性回归/最小平方误差
- 损失函数/代价函数求导法求线性回归
- 一次拟合求线性系统延时
- 逻辑回归(logistic regression)/广义线性回归模型(定义域(-∞,+∞),值域一般离散)
- 概念,特点,用途
- 什么是逻辑回归
- 逻辑回归的优缺点
- 逻辑回归和多重线性回归的区别
- 逻辑回归用途
- 概率知识预备
- 随机变量,随机样本
- 条件概率公式, 乘法公式, 全概率公式
- 贝叶斯公式
- 极大似然估计
- 梯度下降法
- 学习链接
- matlab实现梯度下降功能,求函数f=x^2的最小值
- 逻辑回归算法
- 学习链接
- Regression 常规步骤
- 构造预测函数h(x)
- 逻辑回归2分类
线性回归(定义域(-∞,+∞),值域(-∞,+∞),即输入输出连续)
线性回归/最小平方误差理论
回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
最小二乘法:拟合曲线和数据的误差平方和最小。
实验数据: yi=f(xi) (i=0,1…m)
线性无关函数族: ψ = span{ψ0(x),ψ1(x),…ψn(x)}
一般可取线性无关函数族:= span{1,x,…xn}
拟合曲线:S(x) = a0ψ0(x)+a0ψ0(x)+…anψn(x) (n
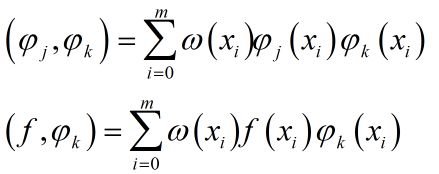
式中:k=0,1,…n. 如若没给权,默认权=1
在线性回归模型中,输出一般是连续的,例如: y=f(x)=ax+b
实质是利用最小二乘法求系数。
MATLAB之线性回归/最小平方误差
% 功能:采用最小二乘法实现最小平方误差(least squares error)/线性回归
% 编辑者:Heart_sea
% 日期:2019,4,28
clear;
clc;
close all;
% ================= import data ==========================================
x = [1,2,3,4,5]';%x坐标
y = [4,4.5,6,8,8.5]';%y坐标
w = [1 1 1 1 1]';% 权,可以理解为在对应的点上重复观测的次数
% ================= 调用 matlab 函数求系数(不加权) =======================
% coef=polyfit(x,y,m); x, y为已知数据点向量, 分别表示横,纵坐标,
% m表示拟合多项式的次数,结果返回m次拟合多项式系数,从高次到低次存放
n = 1; %n次拟合
coef = polyfit(x,y,n);
ybest = polyval(coef,x); %调用MATLAB函数
% a0=coef(1); a1=coef(2);
% ybest=a0*x+a1; % 由线性回归产生的一阶方程式
% ======================== 源方法求系数(加权后) ============================
% 一般可取线性无关函数族:= span{1,x,…xn}
% 这里是线性回归,可取线性函数作拟合曲线,S = a0+a1*x
% 取fai0 = 1, fai1 = x
X0=zeros(n+1,n+1);
Y0=zeros(n+1,1);
%构造矩阵X0
for k0=1:n+1 % 换列
for n0=1:n+1 % 换行
X0(n0,k0)=sum(w.*x.^(k0+n0-2));
end
end
%构造列矩阵y0
for n0 = 1:n+1
Y0(n0,1) = sum(w.*y.*x.^(n0-1));
end
% 矩阵相除求系数
a = X0\Y0;
ybest_w = a(1);
%根据求得的系数初始化并构造多项式方程 ybest_w = a(1)+a(2).*x
for ind = 1:n
ybest_w = ybest_w+a(ind+1)*x.^(ind);
end
% =========== figure =====================================================
plot(x,ybest_w,x,ybest,x,y,'o')
legend('加权后','加权前','原数据')
title('Linear regression estimate')
grid;
损失函数/代价函数求导法求线性回归
% 功能:利用损失函数求导,实现Linear_regression_algorithm 功能
% 编辑者:Heart_sea
% 日期:2019,5,6
clear; % 清除工作区
clc; % 清除命令区
close all; % 清除figure
% ======================= preferences set =================================
X = [1,2,3,4,5]';%x坐标
y = [4,4.5,6,8,8.5]';%y坐标
onesx = ones(length(X),2);
onesx(:, 2) = X;
m = size(onesx,1); % m也就是样本数,size(A,1)返回的是矩阵A所对应的行数
theta0 = 0; % 初始化
theta1 = 0; % 初始化
theta = [theta0, theta1]';% 回归系数
alpha = 0.01; % 步长
Steps = 10000; % 训练步数
% ======================= Linear_regression_algorithm =================================
for k = 1:Steps
theta = theta - (alpha/m) * (deltaFunction(onesx, y, theta))';
costFunc(k) = costFunctionJ(onesx, y, theta);
end
% =================求假设函数
x = 0:max(X);
regressionCurv = theta(1) + theta(2) .* x;
% =================显示theta
disp(theta);
% ======================= figure =================================
figure;
subplot(121);
scatter(X,y,'rx');
hold on;
plot(x,regressionCurv,'b') ;
title('假设函数/回归曲线')
subplot(122);
plot(1:Steps,costFunc);
title('损失函数')
% ======================= 假设函数中递推求和部分 ===========================
function sum = deltaFunction(X, y, theta)%此处的X是传入的onesMat
sum = 0;
for ind = 1:size(X,1)
sum = sum + (X(ind,:) * theta - y(ind)) * X(ind,:);
end
end
% ======================= %代价函数 =======================================
function J = costFunctionJ(X, y, theta)
sqrErrors = (X * theta - y).^2;
m = size(X,1);
J = 1/(2*m) * sum(sqrErrors);
end
上述两种方法,系数相同。(法二训练步数1w步)
一次拟合求线性系统延时
% 功能:通过一次拟合的一次系数求线性系统的延时
% 编辑者:Heart_sea
% 日期:2019,4,26
clear;
clc;
close all;
% ======================= import data ===================================
load('H和f.mat')
% ======================= polyfit函数 ===================================
phi = unwrap(angle(H_temp)); % 相位
p = polyfit(f, phi,1); % 相位作最小二乘法的一次拟合
% ======================= figure ===================================
plot(f,phi,'r-'); % 相位曲线
hold on
plot(f,p(1).*f+p(2),'g--') % 相位线性回归曲线
legend('相位曲线','相位线性回归曲线');
% 可以发现相位曲线和它的线性回归曲线接近重合
delay1 = (p(1).*f+p(2))./(-2*pi*f); % 用相位线性回归曲线求延时
delay2 = phi./(-2*pi.*f); % 用相位公式求延时
% p(2)./(-2*pi*f)数值较小,可约去,故线性相位可用下式估计
delay = p(1)./(-2*pi);
figure;
plot(f,delay1);
hold on;
plot(f,delay2)
legend('用相位线性回归曲线求延时','用相位公式求延时');
逻辑回归(logistic regression)/广义线性回归模型(定义域(-∞,+∞),值域一般离散)
概念,特点,用途
什么是逻辑回归
逻辑回归就是这样的一个过程:面对一个回归或者分类问题,建立代价函数,然后通过优化方法迭代求解出最优的模型参数,然后测试验证我们这个求解的模型的好坏。
Logistic回归虽然名字里带“回归”,但是它实际上是一种分类方法,主要用于两分类问题(即输出只有两种,分别代表两个类别)
回归模型中,y是一个定性变量,比如y=0或1,logistic方法主要应用于研究某些事件发生的概率
逻辑回归的优缺点
优点:
1)速度快,适合二分类问题
2)简单易于理解,直接看到各个特征的权重
3)能容易地更新模型吸收新的数据
缺点:
对数据和场景的适应能力有局限性,不如决策树算法适应性那么强
逻辑回归和多重线性回归的区别
Logistic回归与多重线性回归实际上有很多相同之处,最大的区别就在于它们的因变量不同,其他的基本都差不多。正是因为如此,这两种回归可以归于同一个家族,即广义线性模型(generalizedlinear model)。
这一家族中的模型形式基本上都差不多,不同的就是因变量不同。这一家族中的模型形式基本上都差不多,不同的就是因变量不同。
·如果是连续的,就是多重线性回归
·如果是二项分布,就是Logistic回归
·如果是Poisson分布,就是Poisson回归
·如果是负二项分布,就是负二项回归
逻辑回归用途
·寻找危险因素:寻找某一疾病的危险因素等;
·预测:根据模型,预测在不同的自变量情况下,发生某病或某种情况的概率有多大;
·判别:实际上跟预测有些类似,也是根据模型,判断某人属于某病或属于某种情况的概率有多大,也就是看一下这个人有多大的可能性是属于某病。
概率知识预备
随机变量,随机样本
随机变量:试验之前不能预知,取值随实验结果而定,而试验的结果有一定的概率。
样本定义:
设X是具有分布函数F的随机变量,若X1, X2, X3,… Xn是具有同一分布函数F的、相互独立的随机变量,则称X1, X2, X3,… Xn为从分布函数F得到的容量为n的简单随机样本,简称样本。他们的观察值x1, x2,…xn称为样本值。
可以将样本看成是一个随机变量。
条件概率公式, 乘法公式, 全概率公式
(1)条件概率公式
设A,B是两个事件,且P(B)>0,则在事件B发生的条件下,事件A发生的条件概率(conditional probability)为:
P(A|B)=P(AB)/P(B)
(2)乘法公式
1.由条件概率公式得:
P(AB)=P(A|B)P(B)=P(B|A)P(A)
上式即为乘法公式;
2.乘法公式的推广:对于任何正整数n≥2,当P(A1A2…An-1) > 0 时,有:
P(A1A2...An-1An)=P(A1)P(A2|A1)P(A3|A1A2)...P(An|A1A2...An-1)
(3)全概率公式
- 如果事件组B1,B2,… 满足
1). B1,B2…两两互斥,即 Bi ∩ Bj = ∅ ,i≠j , i,j=1,2,…,且P(Bi)>0,i=1,2,…;
2). B1∪B2∪…=Ω ,则称事件组 B1,B2,…是样本空间Ω的一个划分
设 B1,B2,…是样本空间Ω的一个划分,A为任一事件,则:

上式即为全概率公式(formula of total probability)
2.全概率公式的意义在于,当直接计算P(A)较为困难,而P(Bi),P(A|Bi) (i=1,2,…)的计算较为简单时,可以利用全概率公式计算P(A)。思想就是,将事件A分解成几个小事件,通过求小事件的概率,然后相加从而求得事件A的概率,而将事件A进行分割的时候,不是直接对A进行分割,而是先找到样本空间Ω的一个个划分B1,B2,…Bn,这样事件A就被事件AB1,AB2,…ABn分解成了n部分,即A=AB1+AB2+…+ABn, 每一Bi发生都可能导致A发生相应的概率是P(A|Bi),由加法公式得
P(A)=P(AB1)+P(AB2)+....+P(ABn)=P(A|B1)P(B1)+P(A|B2)P(B2)+...+P(A|Bn)P(PBn)
例:某车间用甲、乙、丙三台机床进行生产,各台机床次品率分别为5%,4%,2%,它们各自的产品分别占总量的25%,35%,40%,将它们的产品混在一起,求任取一个产品是次品的概率。
解:
25%,35%,40%分别为:P(B1), P(B2), P(B3)
5%,4%,2%分别为:P(A|B1), P(A|B2), P(A|B3)
根据全概率公式定义:
P(A)=25%*5%+4%*35%+2%*40%=0.0345
贝叶斯公式
1.与全概率公式解决的问题相反,贝叶斯公式是建立在条件概率的基础上寻找事件发生的原因(即大事件A已经发生的条件下,分割中的小事件Bi的概率),设B1,B2,…是样本空间Ω的一个划分,则对任一事件A(P(A)>0),有

上式即为贝叶斯公式(Bayes formula),Bi 常被视为导致试验结果A发生的”原因“,P(Bi)(i=1,2,…)表示各种原因发生的可能性大小,故称先验概率;P(Bi|A)(i=1,2…)则反映当试验产生了结果A之后,再对各种原因概率的新认识,故称后验概率。有了后验概率,就能对情况有了进一步了解。
例1:发报台分别以概率0.6和0.4发出信号“∪”和“—”。由于通信系统受到干扰,当发出信号“∪”时,收报台分别以概率0.8和0.2收到信号“∪”和“—”;又当发出信号“—”时,收报台分别以概率0.9和0.1收到信号“—”和“∪”。求当收报台收到信号“∪”时,发报台确系发出“∪”的概率。
解:
信号收到 U :A1
信号收到 - :A2
发报台发出U:B1
发报台发出 -:B2
所以,
P(B1) = 0.6, P(B2) = 0.4
P(A1|B1) = 0.8, P(A2|B1) = 0.2
P(A1|B2) = 0.1, P(A2|B2) = 0.9
P(B1|A)=P(A|B1)P(B1) /(P(A1|B1)P(B1)+P(A1|B2)P(B2)) = (0.6*0.8)/(0.6*0.8+0.4*0.1)=0.923
例2. 在夏季,某公园男性穿凉鞋的概率为1/2,女性穿凉鞋的概率为2/3,并且该公园中男女比例通常为2:1,问题:若你在公园中随机遇到一个穿凉鞋的人,请问他的性别为男性或女性的概率分别为多少?
从问题看,就是上面讲的,某事发生了,它属于某一类别的概率是多少?即后验概率。
设:
![]()
由已知可得:
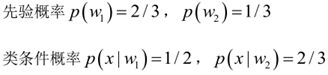
男性和女性穿凉鞋相互独立,所以
![]()
由贝叶斯公式算出:
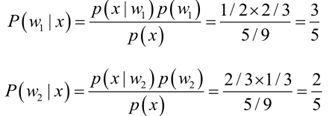
极大似然估计
最大似然估计的目的就是:利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。
原理:极大似然估计是建立在极大似然原理的基础上的一个统计方法,是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。通过若干次试验,观察其结果,利用试验结果得到某个参数值能够使样本出现的概率为最大,则称为极大似然估计。
1.求极大似然函数估计值的一般步骤:
(1) 写出似然函数;
(2) 对似然函数取对数,并整理;
(3) 求导数 ;
(4) 解似然方程
(1)写出似然函数
由于样本集中的样本都是独立分布,可以只考虑一类样本集D,来估计参数向量θ。记已知的样本集为:
D={x1,x2…xN}
似然函数(linkehood function):联合概率密度函数p(D|θ)称为相对于{x1,x2…,xN}的θ的似然函数。
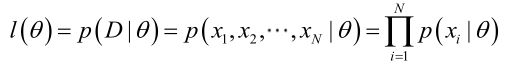
![]()
极大似然估计值:
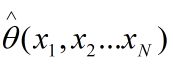
而相应的统计量:

称为参数θ的最大似然估计量,它是样本集的函数
(2)求解似然函数
ML估计:求使得出现该组样本的概率最大的θ值。
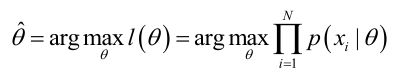
由于l(θ) 与 ln l(θ)在同一θ处取到极值,定义了对数似然函数:
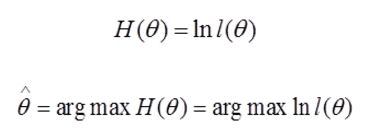
- 未知参数只有一个(θ为标量)
在似然函数满足连续、可微的正则条件下,极大似然估计量是下面微分方程的解:

2. 未知参数有多个(θ为向量)
则θ可表示为具有S个分量的未知向量:
![]()
记梯度算子:

若似然函数满足连续可导的条件,则最大似然估计量就是如下方程的解。

方程的解只是一个估计值,只有在样本数趋于无限多的时候,它才会接近于真实值。
例1:设样本服从正态分布
![]()
则似然函数为:
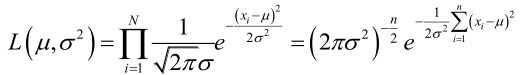
它的对数:
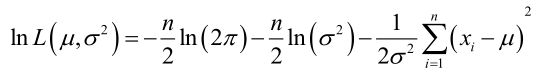
求导,得方程组:
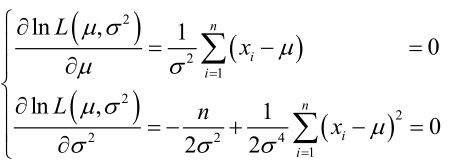
联合解得:



梯度下降法
学习链接
https://baike.baidu.com/item/梯度下降/4864937?fr=aladdin
https://blog.csdn.net/walilk/article/details/50978864
https://baike.baidu.com/item/梯度下降/4864937?fr=aladdin例子
https://www.cnblogs.com/pinard/p/5970503.html
matlab实现梯度下降功能,求函数f=x^2的最小值
% 功能:实现梯度下降功能。求函数f=x^2的最小值
% 编辑者:Heart_sea
% 日期:2019,5,5
clear; % 清除工作区
clc; % 清除命令区
close all; % 清除figure
% ======================= preferences set =================================
% 设置步长为0.2,f_change为改变前后的y值变化,仅设置了一个退出条件。
syms x; %定义符号变量
step = 0.2; %设置步长
x = 2; %初始值
k = 0; %迭代记录数
f_change = x^2; %函数初始化差值
f_current = x^2; %计算当前函数值
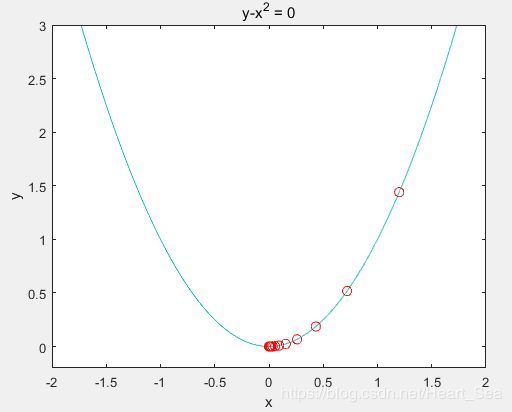
ezplot(@(x,y)y-x.^2) %画出函数图像
axis([-2,2,-0.2,3]) %固定坐标轴
hold on %使当前轴及图像保持而不被刷新,准备接受此后将绘制的图形
while f_change>0.000000001 %设置条件,两次计算的值之差小于某个数,跳出循环
x=x-step*2*x; %-2*x(向量)为梯度反方向,step(标量)为步长
f_change = f_current - x^2; %计算两次函数值之差
f_current = x^2 ; %重新计算当前的函数值
plot(x,f_current,'ro','markersize',7) %标记当前的位置
drawnow; %刷新屏幕
pause(0.2);%程序暂停0.2秒继续执行
k=k+1;
end
hold off %使当前轴及图像不再具备被刷新的性质,新图出现时,取消原图。即,关闭图形保持功能。
fprintf('在迭代%d次后找到函数最小值为%e,对应的x值为%e\n',k,f_current,x)
逻辑回归算法
学习链接
https://blog.csdn.net/lookqlp/article/details/51161640
https://blog.csdn.net/mysteryhaohao/article/details/51240522
https://blog.csdn.net/weixin_30014549/article/details/52850870
https://www.cnblogs.com/sparkwen/p/3441197.html
https://www.cnblogs.com/Belter/p/6128644.html例子
https://blog.csdn.net/chibangyuxun/article/details/53148005公式推导重点
https://blog.csdn.net/lookqlp/article/details/51161640公式推导重点
https://www.cnblogs.com/HolyShine/p/6395965.html线性边界与非线性边界举例
Regression 常规步骤
- 寻找h函数(即预测函数)
- 构造J函数(损失函数)- 根据极大似然估计
- 想办法使得J函数最小并求得回归参数(θ)
而第三步中常见的算法有:
- 梯度下降
- 牛顿迭代算法
- 拟牛顿迭代算法(BFGS算法和L-BFGS算法)
构造预测函数h(x)
% sigmoid函数
% 功能:实现sigmoid函数
% 编辑者:Heart_sea
% 日期:2019,5,5
clear; % 清除工作区
clc; % 清除命令区
close all; % 清除figure
% ======================= sigmoid函数 =====================================
z=[-5 -4 -3 -2 -1 0 1 2 3 4 5];
g=1./(1+exp(-z));
plot(z,g);
grid
% ======================= 坐标轴移动原点位置 ================================
ax = gca;
ax.XAxisLocation = 'origin';
ax.YAxisLocation = 'origin';
ax.Box = 'off';
legend('sigmoid函数')
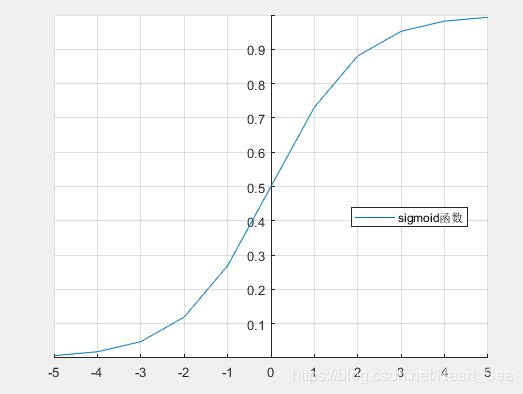
z=0时,S(z) = 0.5
z>0时,S(z) > 0.5
z<0时,S(z) < 0.5
逻辑回归2分类
% 功能:实现Logistic_regression_algorithm 功能
% 编辑者:Heart_sea
% 日期:2019,5,6
clear; % 清除工作区
clc; % 清除命令区
close all; % 清除figure
% ======================= preferences set =================================
x1 = [-5,-4,-2,-2,-3,-1,1,2,4,-6,7,2,2,4,3,5,7,6,8,7,11,12];%横坐标
x2 = [-5,-2,-6,1,2,3,1,-2,-1,7,-4,5,8,6,6,4,7,2,4,5,-1,3]; %纵坐标
X = [x1;x2]';
y = [0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1];
XMat = ones(size(X,1),3);
XMat(:,2:3) = X; % 建立X矩阵
theta0 = 0; % 2分类,有三个系数
theta1 = 0;
theta2 = 0;
theta = [theta0,theta1,theta2]';
alpha = 0.001; % 步长
Steps = 10000; % 训练步数
m = size(X,1); % 样本数量
% ======================= Logistic_regression_algorithm ===================
for k = 1:Steps
theta = theta - alpha * deltaFunction(XMat,y,theta)';
costFunc(k) = costFunctionJ(XMat,y,theta);
end
x = min(x1):0.001:max(x1);
% sigmoid函数的取值为1/2,也就是说取阈值为0.5来划分最后预测的结果
DecisionBoundary = (1/theta(3)) * (-theta(2)*x - theta(1)); % 线性边界
% ======================= figure ==========================================
figure;
set(gcf, 'position', [100 200 1100 400]);
subplot(121);
scatter(x1(1:11),x2(1:11),'rx');
hold on;
scatter(x1(12:22),x2(12:22),'ko');
hold on;
plot(x,DecisionBoundary,'b');
subplot(122);
plot(1:Steps,costFunc);
title('损失函数/代价函数')
% ======================= 代价函数 ========================================
function J = costFunctionJ(X, y,theta)
for i = 1:size(X,1)
if y(i) == 0
cost(i) = -log(1-sigmoid(X(i,:)*theta));
else
cost(i) = -log(sigmoid(X(i,:)*theta));
end
end
m = size(X,1);
J = (1/m) * sum(cost);
end
function r = sigmoid(x)
r = 1/(1+exp(-x));
end
% ======================= 代价函数求偏导部分 ===============================
function sum = deltaFunction(X, y, theta)
sum = 0;
for ind = 1:size(X,1)
sum = sum + (sigmoid(X(ind,:) * theta) - y(ind)) * X(ind,:);
end
end