【操作系统 - 4】动态分区分配算法

操作系统系列

  学习至此，发现很多学了但很久没用的知识，久而久之，慢慢遗忘。等哪天还需要的话，却发现已经忘得差不多了，即使整理了文档（word等），还是得从头再学一遍。读研第一学期，发现很多东西都可以从博客上学习到，也有不少博主呕心沥血整理了挺多有用的博文。于是，本人借此契机，也慢慢开始整理一些博文，不断改进完善中。整理博文（IT）有如下目的：

• 首要目的：记录“求学生涯”的所学所悟，不断修改，不断更新！（有读者的互动）
• 其次目的：在这“开源”的时代，整理并分享所学所悟是一种互利的行为！

博文系列：操作系统课程所学相关算法

• 1.先来先服务FCFS和短作业优先SJF进程调度算法
  
• 2.时间片轮转RR进程调度算法
  
• 3.预防进程死锁的银行家算法
  
• 4.动态分区分配算法
  
• 5.虚拟内存页面置换算法
  
• 6.磁盘调度算法
  

分享目的：希望大家能纠正本人的不足，继续完善程序，共同进步。

6个实验相关代码的下载地址：http://download.csdn.net/detail/houchaoqun_xmu/9865648

-------------------------------

动态分区分配算法

一、概念介绍和案例解析

  动态分区分配是根据进程的实际需要，动态地为之分配内存空间。在实现可变分区分配时，将涉及到分区分配中所用的数据结构、分区分配算法和分区的分配与回收操作这样三个问题。

• 分区分配中的数据结构：
  

  为了实现分区分配，系统中必须配置相应的数据结构，用来描述空闲分区和已分配分区的情况，为分配提供依据。常用的数据结构有以下两种形式： 
(1) 空闲分区表。在系统中设置一张空闲分区表，用于记录每个空闲分区的情况。每个空闲分区占一个表目，表目中包括分区序号、分区始址及分区的大小等数据项。
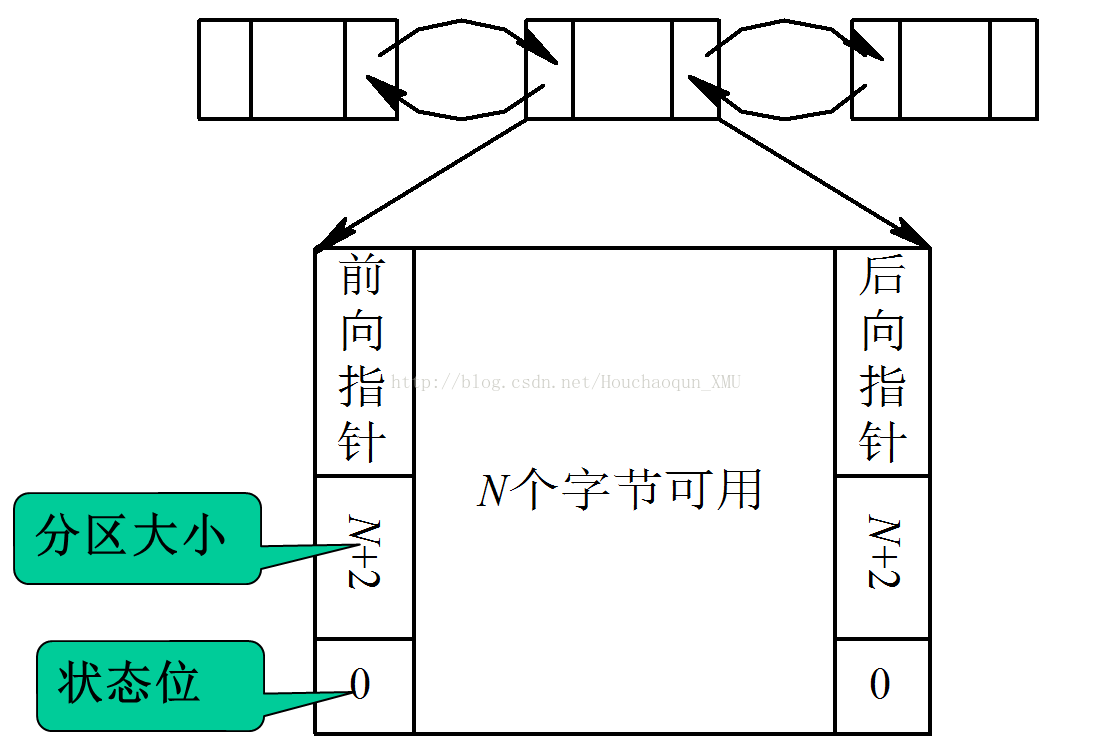
(2) 空闲分区链。为了实现对空闲分区的分配和链接，在每个分区的起始部分，设置一些用于控制分区分配的信息，以及用于链接各分区所用的前向指针；在分区尾部则设置一后向指针，通过前、后向链接指针，可将所有的空闲分区链接成一个双向链，如下图所示：

  为了检索方便，在分区尾部重复设置状态位和分区大小表目。当分区被分配出去以后，把状态位由“0”改为“1”，此时，前、后向指针已无意义。

• 分区分配算法：
  

1) 首次适应算法(First Fit)
  我们以空闲分区链为例来说明采用FF算法时的分配情况。FF算法要求空闲分区链以地址递增的次序链接。
  -- 在分配内存时，从链首开始顺序查找，直至找到一个大小能满足要求的空闲分区为止；
  -- 然后再按照作业的大小，从该分区中划出一块内存空间分配给请求者，余下的空闲分区仍留在空闲链中。
  -- 若从链首直至链尾都不能找到一个能满足要求的分区，则此次内存分配失败，返回。

  首次适应算法倾向于优先利用内存中低址部分的空闲分区，从而保留了高址部分的大空闲区。这给为以后到达的大作业分配大的内存空间创造了条件。其缺点是低址部分不断被划分，会留下许多难以利用的、很小的空闲分区，而每次查找又都是从低址部分开始，这无疑会增加查找可用空闲分区时的开销。

2) 循环首次适应算法(Next Fit)
  该算法是由首次适应算法演变而成的。在为进程分配内存空间时，不再是每次都从链首开始查找，而是从上次找到的空闲分区的下一个空闲分区开始查找，直至找到一个能满足要求的空闲分区，从中划出一块与请求大小相等的内存空间分配给作业。
  为实现该算法，应设置一起始查寻指针，用于指示下一次起始查寻的空闲分区，并采用循环查找方式，即如果最后一个(链尾)空闲分区的大小仍不能满足要求，则应返回到第一个空闲分区，比较其大小是否满足要求。找到后，应调整起始查寻指针。
  该算法能使内存中的空闲分区分布得更均匀，从而减少了查找空闲分区时的开销，但这样会缺乏大的空闲分区。 

3) 最佳适应算法(Best Fit)
  所谓“最佳”是指每次为作业分配内存时，总是把能满足要求、又是最小的空闲分区分配给作业，避免“大材小用”。为了加速寻找，该算法要求将所有的空闲分区按其容量以从小到大的顺序形成一空闲分区链。这样，第一次找到的能满足要求的空闲区，必然是最佳的。
  孤立地看，最佳适应算法似乎是最佳的，然而在宏观上却不一定。因为每次分配后所切割下来的剩余部分总是最小的，这样，在存储器中会留下许多难以利用的小空闲区。 

4) 最坏适应算法(Worst Fit)
  最坏适应分配算法要扫描整个空闲分区表或链表，总是挑选一个最大的空闲区分割给作业使用，其优点是可使剩下的空闲区不至于太小，产生碎片的几率最小，对中、小作业有利，同时最坏适应分配算法查找效率很高。该算法要求将所有的空闲分区按其容量以从大到小的顺序形成一空闲分区链，查找时只要看第一个分区能否满足作业要求。
  但是该算法的缺点也是明显的，它会使存储器中缺乏大的空闲分区。最坏适应算法与前面所述的首次适应算法、循环首次适应算法、最佳适应算法一起，也称为顺序搜索法。 

5) 快速适应算法(Quick Fit)
  该算法又称为分类搜索法，是将空闲分区根据其容量大小进行分类，对于每一类具有相同容量的所有空闲分区，单独设立一个空闲分区链表，这样，系统中存在多个空闲分区链表，同时在内存中设立一张管理索引表，该表的每一个表项对应了一种空闲分区类型，并记录了该类型空闲分区链表表头的指针。
  空闲分区的分类是根据进程常用的空间大小进行划分，如2 KB、4 KB、8 KB等，对于其它大小的分区，如7 KB这样的空闲区，既可以放在8 KB的链表中，也可以放在一个特殊的空闲区链表中。 

  该算法的优点是查找效率高，仅需要根据进程的长度，寻找到能容纳它的最小空闲区链表，并取下第一块进行分配即可。另外该算法在进行空闲分区分配时，不会对任何分区产生分割，所以能保留大的分区，满足对大空间的需求，也不会产生内存碎片。
  该算法的缺点是在分区归还主存时算法复杂，系统开销较大。
  此外，该算法在分配空闲分区时是以进程为单位，一个分区只属于一个进程，因此在为进程所分配的一个分区中，或多或少地存在一定的浪费。空闲分区划分越细，浪费则越严重，整体上会造成可观的存储空间浪费，这是典型的以空间换时间的作法。 

• 分区分配操作：
  

3．分区分配操作
  1) 分配内存
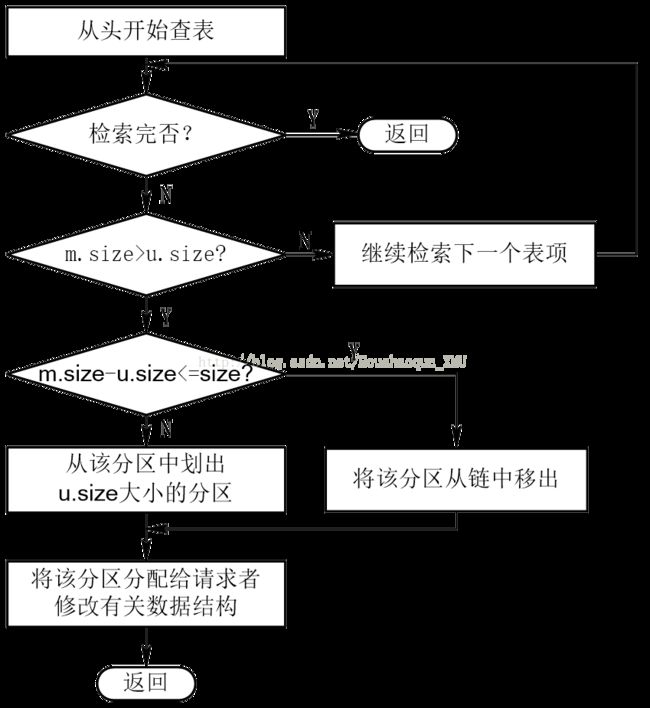
  系统应利用某种分配算法，从空闲分区链(表)中找到所需大小的分区。
  设请求的分区大小为u.size，表中每个空闲分区的大小可表示为m.size。若m.size-u.size≤size(size是事先规定的不再切割的剩余分区的大小)，说明多余部分太小，可不再切割，将整个分区分配给请求者；
  否则(即多余部分超过size)，从该分区中按请求的大小划分出一块内存空间分配出去，余下的部分仍留在空闲分区链(表)中。然后，将分配区的首址返回给调用者。

2) 回收内存
  当进程运行完毕释放内存时，系统根据回收区的首址，从空闲区链(表)中找到相应的插入点，此时可能出现以下四种情况之一：
  (1) 回收区与插入点的前一个空闲分区F1相邻接，见图4-8(a)。此时应将回收区与插入点的前一分区合并，不必为回收分区分配新表项，而只需修改其前一分区F1的大小，大小为两者之和。
  (2) 回收分区与插入点的后一空闲分区F2相邻接，见图4-8(b)。此时也可将两分区合并，形成新的空闲分区，但用回收区的首址作为新空闲区的首址，大小为两者之和。 

  (3) 回收区同时与插入点的前、后两个分区邻接，见图4-8(c)。此时将三个分区合并，使用F1的表项和F1的首址，取消F2的表项，大小为三者之和。
  (4) 回收区既不与F1邻接，又不与F2邻接。这时应为回收区单独建立一新表项，填写回收区的首址和大小，并根据其首址插入到空闲链中的适当位置。 

  

二、实验介绍

• 问题描述：

  设计程序模拟四种动态分区分配算法：首次适应算法、循环首次适应算法、最佳适应算法和最坏适应算法的工作过程。假设内存中空闲分区个数为n，空闲分区大小分别为P1, … ,Pn，在动态分区分配过程中需要分配的进程个数为m（m≤n），它们需要的分区大小分别为S1, … ,Sm，分别利用四种动态分区分配算法将m个进程放入n个空闲分区，给出进程在空闲分区中的分配情况。

• 程序要求：

1）利用首次适应算法、循环首次适应算法、最佳适应算法和最坏适应算法四种动态分区分配算法模拟分区分配过程。
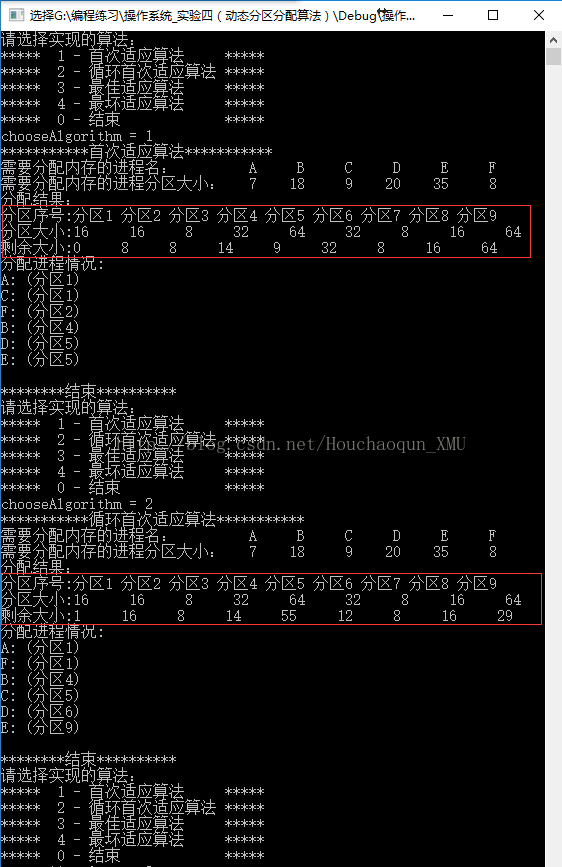
2）模拟四种算法的分区分配过程，给出每种算法进程在空闲分区中的分配情况。
3）输入：空闲分区个数n，空闲分区大小P1, … ,Pn，进程个数m，进程需要的分区大小S1, … ,Sm，算法选择1-首次适应算法，2-循环首次适应算法，3-最佳适应算法，4-最坏适应算法。
4）输出：最终内存空闲分区的分配情况。

三、程序设计和程序开发

• 算法思想：

  本程序采用空闲分区表的方式实现，借助数组以及相应的数据结构实现了“首次适应算法”，“循环首次适应算法”，“最佳适应算法”，“最坏适应算法”，其中“最佳适应算法”和“最坏适应算法”需要对分区进行排序，故需要相应的数据结构来保证排序后所对应的分区序列号保持与原分区一致。
  本程序的排序采用冒泡算法，根据排序算法的选择的不同，因其稳定性的不同，会有细微的差别，但不影响算法的实现。

• 核心算法：

void FirstFit()
{
	cout<<"***********首次适应算法***********"<

void NextFit()
{
	cout<<"***********循环首次适应算法***********"<= LeftProcessNeed[i])
			{
				LeftFreePartition[nextPoint] -= LeftProcessNeed[i];
				LeftProcessNeed[i] = 0;
				NameProcessToPartition[i][nextPoint] = ProcessName[i];
				nextPoint++;
				if (nextPoint > PartitionNum - 1)
				{
					nextPoint = 0;  //当j遍历到分区末尾的时候，返回首位置
				}
				isWhile = false;
			}
			else
				nextPoint++;
		}
	}
	display();
}

void BestFit()
{
	//思想：利用冒泡排序对分区大小进行排序，但不改变原分区的位置
	//创建一个结构体，包括分区大小和所对应的id，排序过程中，每改变顺序一次，id随着改变
	//关键：每次分配完一个进程的内存大小后，都要重新排序
	cout<<"***********最佳适应算法***********"< 0;s--)   //冒泡排序(每次分配完一个进程后，都需要重新排序)
		{
			for (int t = 0;t < s;t++)
			{
				if (best[s].partitionSize < best[t].partitionSize)
				{
					temp = best[s].partitionSize;
					best[s].partitionSize = best[t].partitionSize;
					best[t].partitionSize = temp;

					tempID = best[s].id;
					best[s].id = best[t].id;
					best[t].id = tempID;
				}
			}
		}

		for (j = 0;j

void WorstFit()
{
	cout<<"***********最坏适应算法***********"<0;s--)
		{
			for (t = 0; t Worst[t].partitionSize)
				{
					tempSize = Worst[s].partitionSize;
					Worst[s].partitionSize = Worst[t].partitionSize;
					Worst[t].partitionSize = tempSize;

					tempID = Worst[s].id;
					Worst[s].id = Worst[t].id;
					Worst[t].id = tempID;
				}
			}
		}

		for (j = 0;j

四、实验结果分析

• 测试数据：

9
16 16 8 32 64 32 8 16 64


6
A B C D E F
7 18 9 20 35 8

• 实验结果：

五、实验源码

// 操作系统_实验四（动态分区分配算法）.cpp : 定义控制台应用程序的入口点。
//

#include 
#include 
#include 
using namespace std;

#define MAXNUMBER 100
static int PartitionNum;  //内存中空闲分区的个数
static int ProcessNum; //需要分配的进程个数
static int FreePartition[MAXNUMBER];  //空闲分区对应的内存
static int ProcessNeed[MAXNUMBER];  //需要分配的进程大小

static int LeftFreePartition[MAXNUMBER];
static int LeftProcessNeed[MAXNUMBER];

static char ProcessName[MAXNUMBER];
static char NameProcessToPartition[MAXNUMBER][MAXNUMBER];

typedef struct
{
	int partitionSize;
	int id;
}sortNeed;

void readDataFunction();
void display();
void FirstFit();
void NextFit();
void BestFit();
void WorstFit();
void selectAlgorithm(int chooceAlgorithm);
void display();

void readDataFunction()
{
	ifstream readData;
	readData.open("data.txt");

	readData>>PartitionNum;
	for (int i=0;i>FreePartition[i];
	}

	readData>>ProcessNum;
	for (int i=0;i>ProcessName[i];
	}
	for (int i=0;i>ProcessNeed[i];
	}
}

void initial()
{
	readDataFunction();   //读取原始数据
	for (int i=0;i= LeftProcessNeed[i])
			{
				LeftFreePartition[nextPoint] -= LeftProcessNeed[i];
				LeftProcessNeed[i] = 0;
				NameProcessToPartition[i][nextPoint] = ProcessName[i];
				nextPoint++;
				if (nextPoint > PartitionNum - 1)
				{
					nextPoint = 0;  //当j遍历到分区末尾的时候，返回首位置
				}
				isWhile = false;
			}
			else
				nextPoint++;
		}
	}
	display();
}

void BestFit()
{
	//思想：利用冒泡排序对分区大小进行排序，但不改变原分区的位置
	//创建一个结构体，包括分区大小和所对应的id，排序过程中，每改变顺序一次，id随着改变
	//关键：每次分配完一个进程的内存大小后，都要重新排序
	cout<<"***********最佳适应算法***********"< 0;s--)   //冒泡排序(每次分配完一个进程后，都需要重新排序)
		{
			for (int t = 0;t < s;t++)
			{
				if (best[s].partitionSize < best[t].partitionSize)
				{
					temp = best[s].partitionSize;
					best[s].partitionSize = best[t].partitionSize;
					best[t].partitionSize = temp;

					tempID = best[s].id;
					best[s].id = best[t].id;
					best[t].id = tempID;
				}
			}
		}

		for (j = 0;j0;s--)
		{
			for (t = 0; t Worst[t].partitionSize)
				{
					tempSize = Worst[s].partitionSize;
					Worst[s].partitionSize = Worst[t].partitionSize;
					Worst[t].partitionSize = tempSize;

					tempID = Worst[s].id;
					Worst[s].id = Worst[t].id;
					Worst[t].id = tempID;
				}
			}
		}

		for (j = 0;j