python Numpy中求向量和矩阵的范数

转载 https://blog.csdn.net/qq_35154529/article/details/82754157

np.linalg.norm(求范数):linalg=linear（线性）+algebra（代数），norm则表示范数。

函数参数

x_norm=np.linalg.norm(x, ord=None, axis=None, keepdims=False)

①x: 表示矩阵（也可以是一维）

②ord：范数类型

向量的范数：

矩阵的范数：

ord=1：列和的最大值

ord=2：|λE-ATA|=0，求特征值，然后求最大特征值得算术平方根

ord=∞：行和的最大值

③axis：处理类型

axis=1表示按行向量处理，求多个行向量的范数

axis=0表示按列向量处理，求多个列向量的范数

axis=None表示矩阵范数。

④keepding：是否保持矩阵的二维特性

True表示保持矩阵的二维特性，False相反

向量范数:

1-范数：，即向量元素绝对值之和，matlab调用函数norm(x, 1) 。

2-范数：，Euclid范数（欧几里得范数，常用计算向量长度），即向量元素绝对值的平方和再开方，matlab调用函数norm(x, 2)。

∞-范数：，即所有向量元素绝对值中的最大值，matlab调用函数norm(x, inf)。

-∞-范数：，即所有向量元素绝对值中的最小值，matlab调用函数norm(x, -inf)。

p-范数：，即向量元素绝对值的p次方和的1/p次幂，matlab调用函数norm(x, p)。

矩阵范数:

1-范数：， 列和范数，即所有矩阵列向量绝对值之和的最大值，matlab调用函数norm(A, 1)。

2-范数：，谱范数，即A’A矩阵的最大特征值的开平方。matlab调用函数norm(x, 2)。

∞-范数：，行和范数，即所有矩阵行向量绝对值之和的最大值，matlab调用函数norm(A, inf)。

F-范数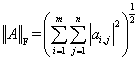：，Frobenius范数，即矩阵元素绝对值的平方和再开平方，matlab调用函数norm(A, ’fro‘)。

import numpy as np

x1=np.array([1,5,6,3,-1])
x2=np.arange(12).reshape(3,4)
print x1,’\n’,x2
print ‘向量2范数:’
print np.linalg.norm(x1)
print np.linalg.norm(x1,ord=2)
print ‘默认的矩阵范数:’
print np.linalg.norm(x2)
print ‘矩阵2范数:’
print np.linalg.norm(x2,ord=2)

经测试知：

np.linalg.norm(X),X为向量时，默认求向量2范数，即求向量元素绝对值的平方和再开方；

X为矩阵是，默认求的是F范数。矩阵的F范数即：矩阵的各个元素平方之和再开平方根，它通常也叫做矩阵的L2范数，它的有点在它是一个凸函数，可以求导求解，易于计算。

作者：104109121
来源：CSDN
原文：https://blog.csdn.net/qq_35154529/article/details/82754157
版权声明：本文为博主原创文章，转载请附上博文链接！