算法浅谈

最近在研究算法，看到这么一句话感触挺深刻，不讲时间复杂度的算法都是耍流氓，感觉挺有趣的，其实也就是这么回事，研究算法主要目的是研究时间的复杂度，若算法中不谈时间的复杂度，没有任何意义。

算法的定义：

• 有穷性 ：就是说必须在人类毁灭前结束
• 确定性：举个例子，老板便宜一点，那么这个一点是多少，所以必须确定
• 可行性：比如造个飞碟（你这么厉害你家里人造么）
• 输入&输出

那么我们来介绍一下有什么算法：

1. 穷举法（万能算法）
2. 分而治之（减而治之）
   1. 二分查找-减而治之
   2. 归并排序-分而治之
3. 贪心算法
4. 动态规划
   1. 背包问题
   2. 士兵路径

然后我们接下来讲下时间复杂度的计算，因为谈算法必须讲时间复杂度

一、定义（理解不了没关系，理解得了还写什么博客）

     一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n)，使得当n趋近于无穷大时，T(n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n))，称O(f(n))为算法的渐进时间复杂度(O是数量级的符号 )，简称时间复杂度。

（1）时间频度 

    一个算法执行所耗费的时间，从理论上是不能算出来的，必须上机运行测试才能知道。但我们不可能也没有必要对每个算法都上机测试，只需知道算法花费的时间多少（魔镜魔镜告诉我，那个算法是跑得快的算法0.0）

    一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。

    一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。

 

（2）时间复杂度 

     n称为问题的规模，当n不断变化时，时间频度T(n)也会不断变化。但有时我们想知道它变化时呈现什么规律。为此，我们引入时间复杂度概念。 

     一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n),使得当n趋近于无穷大时，T（n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=Ｏ(f(n))

    称Ｏ(f(n)) 为算法的渐进时间复杂度，简称时间复杂度。

     注意，时间频度与时间复杂度是不同的，时间频度不同但时间复杂度可能相同。

如：T(n)=n^2+3n+4与T(n)=4n2+2n+1它们的频度不同，但时间复杂度相同，都为O(n^2)。

 

3）最坏时间复杂度和平均时间复杂度 　最坏情况下的时间复杂度称最坏时间复杂度。一般不特别说明，讨论的时间复杂度均是最坏情况下的时间复杂度。 这样做的原因是：最坏情况下的时间复杂度是算法在任何输入实例上运行时间的上界，这就保证了算法的运行时间不会比任何更长。

     在最坏情况下的时间复杂度为T(n)=0(n)，它表示对于任何输入实例,该算法的运行时间不可能大于0(n)。 平均时间复杂度是指所有可能的输入实例均以等概率出现的情况下，算法的期望运行时间。

指数阶0(2n)，显然，时间复杂度为指数阶0(2n)的算法效率极低，当n值稍大时就无法应用。

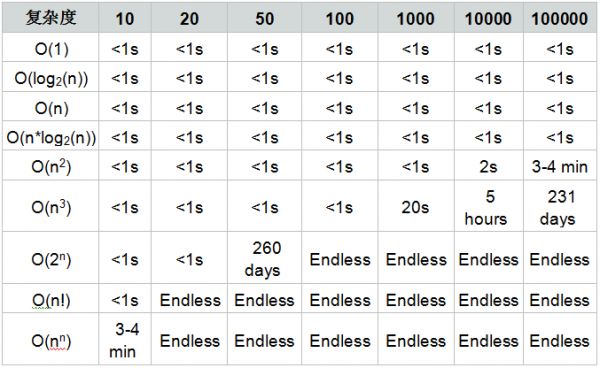
我们来看下常见的时间复杂度：

常数阶O(1)<对数阶O(log2n)<线性阶O(n),<线性对数阶O(nlog2n)

<平方阶O(n^2)<方阶O(n3)

<指数阶O(2^n)

接下来看几个例子，更好的理解

常数阶 
先举了例子，如下所示。

  int sum = 0,n = 100; //执行一次  
  sum = (1+n)*n/2; //执行一次  
  System.out.println (sum); //执行一次 

上面算法的运行的次数的函数为f(n)=3，根据推导大O阶的规则1，我们需要将常数3改为1，则这个算法的时间复杂度为O(1)。如果sum = （1+n）*n/2这条语句再执行10遍，因为这与问题大小n的值并没有关系，所以这个算法的时间复杂度仍旧是O(1)，我们可以称之为常数阶。

线性阶 
线性阶主要要分析循环结构的运行情况，如下所示。

for(int i=0;i

上面算法循环体中的代码执行了n次，因此时间复杂度为O(n)。

对数阶 
接着看如下代码：

int number=1;
while(number

可以看出上面的代码，随着number每次乘以2后，都会越来越接近n，当number不小于n时就会退出循环。假设循环的次数为X，则由2^x=n得出x=log₂n，因此得出这个算法的时间复杂度为O(logn)。

平方阶 
下面的代码是循环嵌套：

 for(int i=0;i

内层循环的时间复杂度在讲到线性阶时就已经得知是O(n)，现在经过外层循环n次，那么这段算法的时间复杂度则为O(n²)。 
接下来我们来算一下下面算法的时间复杂度：

for(int i=0;i

需要注意的是内循环中int j=i，而不是int j=0。当i=0时，内循环执行了n次；i=1时内循环执行了n-1次，当i=n-1时执行了1次，我们可以推算出总的执行次数为：

n+(n-1)+(n-2)+(n-3)+……+1 
=(n+1)+[(n-1)+2]+[(n-2)+3]+[(n-3)+4]+…… 
=(n+1)+(n+1)+(n+1)+(n+1)+…… 
=(n+1)n/2 
=n(n+1)/2 
=n²/2+n/2

根据此前讲过的推导大O阶的规则的第二条：只保留最高阶，因此保留n²/2。根据第三条去掉和这个项的常数，则去掉1/2,最终这段代码的时间复杂度为O(n²)。

综上：

1、取决于执行次数最多的语句，如当有若干个循环语句时，算法的时间复杂度是由嵌套层数最多的循环语句中最内层语句的频度f(n)决定的。

2、如果算法的执行时间不随着问题规模n的增加而增长，即使算法中有上千条语句，其执行时间也不过是一个较大的常数。此类算法的时间复杂度是O(1)

3、算法的时间复杂度不仅仅依赖于问题的规模，还与输入实例的初始状态有关。