一篇读懂生成对抗网络（GAN）原理+tensorflow代码实现(花费10分钟，不要急躁)

作者：JASON
2017.10.15

10分钟把故事说完！

---

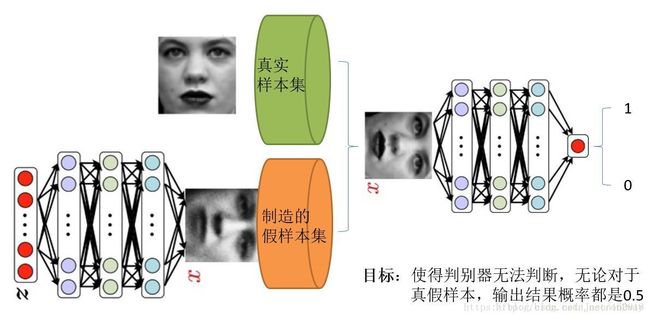
  生成对抗网络GAN（Generative adversarial networks）是最近很火的深度学习方法，要理解它可以把它分成生成模型和判别模型两个部分，简单来说就是：两个人比赛，看是 A 的矛厉害，还是 B 的盾厉害。比如，有一个业余画家总喜欢仿造著名画家的画，把仿造的画和真实的画混在一起，然后有一个专家想办法来区分那些是真迹，那些是赝品。通过不断的相互博弈，业余画家的仿造能力日益上升，与此同时，通过不断的判断结果反馈，积累了不少经验，专家的鉴别能力也在上升，进一步促使业余专家的仿造能力大幅提升，最后使得业余专家的仿造作品无限接近与真迹，使得鉴别专家无法辨别，最后判断的准确率为0.5。

  总的来说，Goodfellow等人提出的GAN是通过对抗过程来估计生成模型的框架。在这种框架下，我们需要同时训练两个网络，即一个能获取数据分布的生成模型G和一个估计数据来源于真实样本概率的判别模型D。生成器的训练目的是最大化判别器犯错误的概率，而判别器的训练过程是最小化犯错误的概率。因此这一过程存在一个极大极小博弈（minimax game）。在所有可能的G和D函数中，存在一个唯一均衡解。即生成模型可以生成训练样本相同的数据分布，而此时判别模型的概率处处为1/2。

  当模型都为多层感知机时，对抗性建模框架可以最直接地应用。为了学习到生成器在数据 x 上的分布 P_g，我们先定义一个先验的输入噪声变量 P_z(z)，然后根据 G(z;θ_g) 将其映射到数据空间中，其中 G 为多层感知机所表征的可微函数。我们同样需要定义第二个多层感知机 D(s;θ_d)，它的输出为单个标量。D(x) 表示 x 来源于真实数据而不是 P_g 的概率。我们训练 D 以最大化正确分配真实样本和生成样本的概率，因此我们就可以通过最小化 log(1-D(G(z))) 而同时训练 G。也就是说判别器 D 和生成器G对价值函数 V(G,D) 进行了极小极大化博弈：

  此外，Goodfellow 等人在论文中使用如下案例为我们简要介绍了基本概念。

  如上图所示，生成对抗网络会训练并更新判别分布（即 D，蓝色的虚线），更新判别器后就能将数据真实分布（黑点组成的线）从生成分布 P_g(G)（绿色实线）中判别出来。下方的水平线代表采样域 Z，其中等距线表示 Z 中的样本为均匀分布，上方的水平线代表真实数据 X 中的一部分。向上的箭头表示映射 x=G(z) 如何对噪声样本（均匀采样）施加一个不均匀的分布 P_g。(a)考虑在收敛点附近的对抗训练：P_g 和 P_data 已经十分相似，D 是一个局部准确的分类器。(b)在算法内部循环中训练 D 以从数据中判别出真实样本，该循环最终会收敛到 D(x)=P_data(x)/(P_data(x)+P_g(x))。©随后固定判别器并训练生成器，在更新 G 之后，D 的梯度会引导 G(z)流向更可能被 D 分类为真实数据的方向。(d)经过若干次训练后，如果 G 和 D 有足够的复杂度，那么它们就会到达一个均衡点。这个时候 P_g=P_data，即生成器的概率密度函数等于真实数据的概率密度函数，也即生成的数据和真实数据是一样的。在均衡点上 D 和 G 都不能得到进一步提升，并且判别器无法判断数据到底是来自真实样本还是伪造的数据，即 D(x)= 1/2。
  上面是比较精简地介绍了生成对抗网络的基本概念，下一节将会把这些概念形式化，并描述优化的大致过程。

概念与过程的形式化

1. 理论完美的生成器

  该算法的目标是令生成器生成与真实数据几乎没有区别的样本，即一个造假一流的 A，就是我们想要的生成模型。数学上，即将随机变量生成为某一种概率分布，也可以说概率密度函数为相等的：P_G(x)=P_data(x)。这正是数学上证明生成器高效性的策略：即定义一个最优化问题，其中最优生成器 G 满足 P_G(x)=P_data(x)。如果我们知道求解的 G 最后会满足该关系，那么我们就可以合理地期望神经网络通过典型的 SGD 训练就能得到最优的 G。

2. 最优化问题

  正如最开始我们了解的警察与造假者案例，定义最优化问题的方法就可以由以下两部分组成。首先我们需要定义一个判别器 D 以判别样本是不是从 P_data(x) 分布中取出来的，因此有：

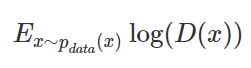
  其中 E 指代取期望。这一项是根据「正类」（即辨别出 x 属于真实数据 data）的对数损失函数而构建的。最大化这一项相当于令判别器 D 在 x 服从于 data 的概率密度时能准确地预测 D(x)=1，即：

  另外一项是企图欺骗判别器的生成器 G。该项根据「负类」的对数损失函数而构建，即：

  因为 x<1 的对数为负，那么如果最大化该项的值，则需要令均值 D(G(z))≈0，因此 G 并没有欺骗 D。为了结合这两个概念，判别器的目标为最大化：

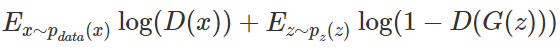
  给定生成器 G，其代表了判别器 D 正确地识别了真实和伪造数据点。给定一个生成器 G，上式所得出来的最优判别器可以表示为 （下文用 D_G表示）。定义价值函数为：

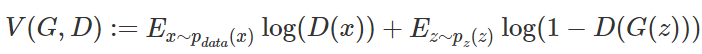
  然后我们可以将最优化问题表述为：

  现在 G 的目标已经相反了，当 D=D_G时，最优的 G 为最小化前面的等式。在论文中，作者更喜欢求解最优化价值函的 G 和 D 以求解极小极大博弈：

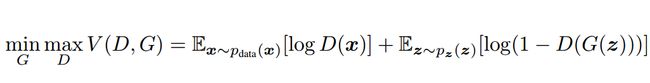
  对于 D 而言要尽量使公式最大化（识别能力强），而对于 G 又想使之最小（生成的数据接近实际数据）。整个训练是一个迭代过程。其实极小极大化博弈可以分开理解，即在给定 G 的情况下先最大化 V(D,G) 而取 D，然后固定 D，并最小化 V(D,G) 而得到 G。其中，给定 G，最大化 V(D,G) 评估了 P_G 和 P_data 之间的差异或距离。

最后，我们可以将最优化问题表达为：

  上文给出了 GAN 概念和优化过程的形式化表达。通过这些表达，我们可以理解整个生成对抗网络的基本过程与优化方法。本质上，还是通过误差方向传播的方式来更新参数。当然，有了这些概念我们完全可以直接在 GitHub 上找一段 GAN 代码稍加修改并很好地运行它。但如果我们希望更加透彻地理解 GAN，更加全面地理解实现代码，那么我们还需要知道很多推导过程。比如什么时候 D 能令价值函数 V(D,G) 取最大值、G 能令 V(D,G) 取最小值，而 D 和 G 该用什么样的神经网络（或函数），它们的损失函数又需要用什么等等。总之，还有很多理论细节与推导过程需要我们进一步挖掘。

---------------------------
代码实现GAN

Dependencies:
tensorflow: at least 1.1.0
matplotlib
numpy

本次试验项目描述如下：
  让生成器学习如何画一条曲线，不同于其他神经网络框架，GAN要求同时求出生成模型的误差G_LOSS和判别模型的误差D_LOSS,然后再用以下两个训练op去同时训练，其中LR表示学习率。

• Train_G=optimizer(LR).minimize(G_LOSS)
• Train_D=optimizer(LR).minimize(D_LOSS)

  把这两个train_op同时扔到sess.run()里面去训练更新参数

#总的框架：
def artist_works()：#专家画的画
    return paintings

with tf.variable_scope('Generator'):
with tf.variable_scope('Discriminator'):

D_loss = -tf.reduce_mean(tf.log(prob_artist0) + tf.log(1-prob_artist1))
G_loss = tf.reduce_mean(tf.log(1-prob_artist1))
#固定生成器之后，tf.log(prob_artist0)等于一个常数，所以没有加入
train_D = tf.train.AdamOptimizer(LR_D).minimize(D_loss, )
train_G = tf.train.AdamOptimizer(LR_G).minimize(G_loss, )

sess = tf.Session()
sess.run(tf.global_variables_initializer())
for step in range(5000):
    G_paintings, pa0, Dl = sess.run([G_out, prob_artist0, D_loss, train_D, train_G],{G_in: G_ideas, real_art: artist_paintings})[:3]

第一步
设置超参数

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

tf.set_random_seed(1)
np.random.seed(1)

## 设置超参数
BATCH_SIZE = 64		# 批量大小
LR_G = 0.0001           # 生成器的学习率
LR_D = 0.0001           # 判别器的学习率
N_IDEAS = 5             # 认为这是生成5种艺术作品（5种初始化曲线）
ART_COMPONENTS = 15     # 在画上画15个点练成一条线
PAINT_POINTS = np.vstack([np.linspace(-1, 1, ART_COMPONENTS) for _ in range(BATCH_SIZE)])
#列表解析式代替了for循环，PAINT_POINTS.shape=(64,15),
#np.vstack()默认逐行叠加（axis=0）

第二步
专家开始作画

def artist_works():    
    a = np.random.uniform(1, 2, size=BATCH_SIZE)[:, np.newaxis]
    #a为64个1到2均匀分布抽取的值，shape=(64,1)
    paintings = a * np.power(PAINT_POINTS, 2) + (a-1)
    return paintings

第三步
设置生成器网络结构，生成一副业余画家的画

with tf.variable_scope('Generator'):
    G_in = tf.placeholder(tf.float32, [None, N_IDEAS]) # 随机的ideals（来源于正态分布）
    G_l1 = tf.layers.dense(G_in, 128, tf.nn.relu)
    G_out = tf.layers.dense(G_l1, ART_COMPONENTS)      # 生成一副业余专家的画（15个数据点）

第四步
设置判别器网络结构，先输入专家画，返回判断真的概率，再输入业余专家的画，同样返回判为真概率

with tf.variable_scope('Discriminator'):
    """判别器与生成器不同，生成器只需要输入生成的数据就行，它无法接触到专家的画，
    如果能输入专家的画，那就不用学习了，直接导入到判别器就是0.5的概率，换句话说，
    生成器只能通过生成器的误差反馈来调节权重，使得逐渐生成逼真的画出来。"""
	
    # 接受专家的画
    real_art = tf.placeholder(tf.float32, [None, ART_COMPONENTS], name='real_in')   
	
    # 将专家的画输入到判别器，判别器判断这副画来自于专家的概率
    D_l0 = tf.layers.dense(real_art, 128, tf.nn.relu, name='Discri')
    prob_artist0 = tf.layers.dense(D_l0, 1, tf.nn.sigmoid, name='out')  
    
    # 之后输入业余专家的画，G_out代入到判别器中。
    D_l1 = tf.layers.dense(G_out, 128, tf.nn.relu, name='Discri', reuse=True)  
	
    # 代入生成的画，判别器判断这副画来自于专家的概率
    prob_artist1 = tf.layers.dense(D_l1, 1, tf.nn.sigmoid, name='out', reuse=True) 
    """注意到，判别器中当输入业余专家的画时，这层是可以重复利用的，通过动态调整这次的权重来完成判别器的loss最小，关键一步。"""

第五步
定义误差loss

根据公式：

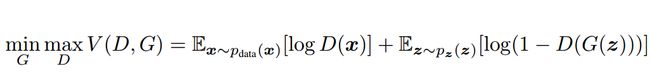
对于D_loss先固定G（生成器），先让判别器学习一下专家的画，对专家的画有了“印象”之后再去接受业余的画，再对D（判别器）上求V的最大值化以此来得到此时的最优解D。由于tensorflow只支持minimize()，所以这里添加“-”号，来转化为求最大值。
对于G_loss先固定D，等同于把logD(X)的期望当作常数，所以只需要最小化后面那一部分即可。

#判别器loss，此时需同时优化两部分的概率
D_loss = -tf.reduce_mean(tf.log(prob_artist0) + tf.log(1-prob_artist1))

#对于生成器的loss，此时prob_artist0是固定的，可以看到生成器并没有输入专家的画，
所以tf.log(prob_artist0)是一个常数，故在这里不用考虑。
G_loss = tf.reduce_mean(tf.log(1-prob_artist1))

第六步
定义Train_D和Train_G

train_D = tf.train.AdamOptimizer(LR_D).minimize(
    D_loss, var_list=tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='Discriminator'))
train_G = tf.train.AdamOptimizer(LR_G).minimize(
    G_loss, var_list=tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope='Generator'))

第七步
定义sess，初始化所以变量

sess = tf.Session()
sess.run(tf.global_variables_initializer())

第八步
画图，实时展示结果

plt.ion()   # 连续画图
for step in range(5000):
    artist_paintings = artist_works()           # 专家的画，每一轮专家的画都是随机生成的！
    G_ideas = np.random.randn(BATCH_SIZE, N_IDEAS)  #业余画家的5个想法
    G_paintings, pa0, Dl = sess.run([G_out, prob_artist0, D_loss, train_D, train_G],
     {G_in: G_ideas, real_art: artist_paintings})[:3]   # 训练和获取结果
                                    
    if step % 50 == 0:  # 每50步训练画一次图
        plt.cla()
        plt.plot(PAINT_POINTS[0], G_paintings[0], c='#4AD631', lw=3, label='生成的画',)
        plt.plot(PAINT_POINTS[0], artist_paintings[0], c='#4AD632', lw=3, label='专家的画',)
        plt.plot(PAINT_POINTS[0], 2 * np.power(PAINT_POINTS[0], 2) + 1, c='#74BCFF', lw=3, label='上限')
        plt.plot(PAINT_POINTS[0], 1 * np.power(PAINT_POINTS[0], 2) + 0, c='#FF9359', lw=3, label='下限')
        plt.text(-.5, 2.3, 'D accuracy=%.2f (0.5 for D to converge)' % pa0.mean(), fontdict={'size': 15})
        plt.text(-.5, 2, 'D score= %.2f (-1.38 for G to converge)' % -Dl, fontdict={'size': 15})
        plt.ylim((0, 3)); plt.legend(loc='upper right', fontsize=12); plt.draw(); plt.pause(0.01)

plt.ioff()
plt.show()

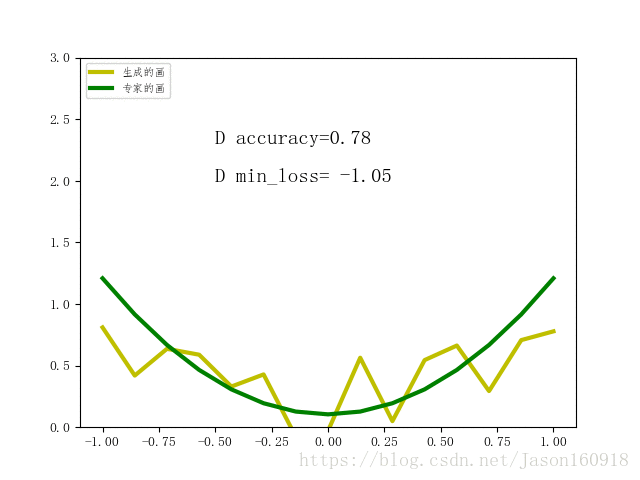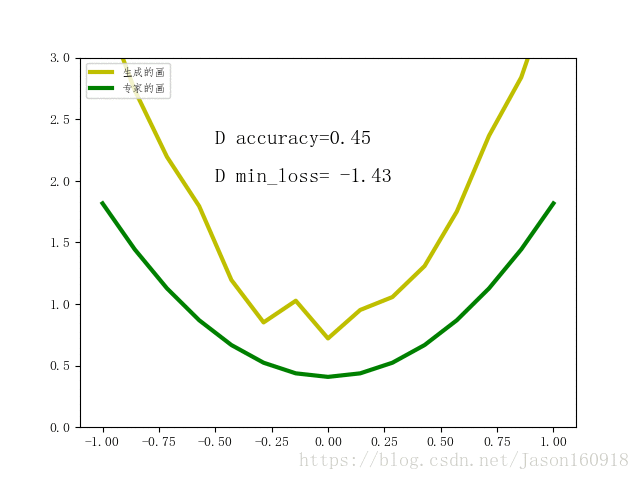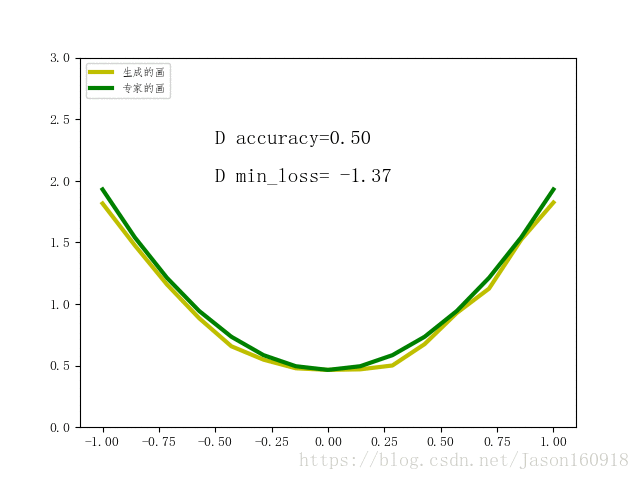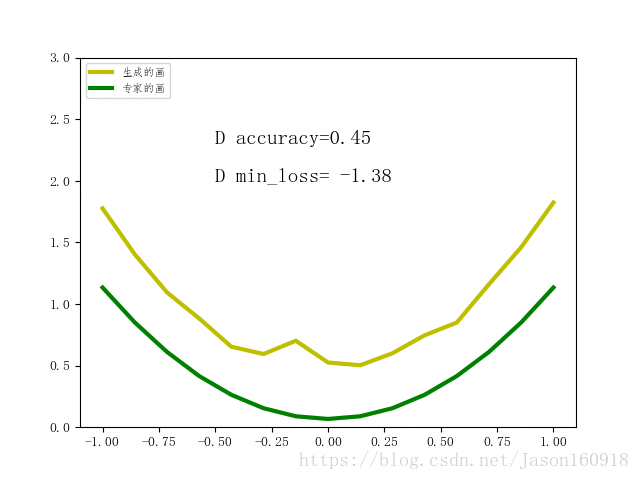
最终结果展示：

  如上图所示，绿色曲线是专家的画，每一轮都会随机重新生成，黄色曲线是业余画家的画。可以看到，随着训练的进行，通过不段学习和模仿专家的画，黄的曲线逐渐变得像绿色曲线一样的弯曲，并最终使得判断器或者生成器输出的概率=0.5,已经无法分辨到底是专家的画还是业余画家的画。如果增加epoch的话，理论上可以使它趋近于0.5，判别误差收敛于-1.38。

点赞是我继续分享的动力，源码可以直接运行，谢谢大家！