K-means聚类matlab实现

K-means

kmeans用贪心策略，能十分简单有效的聚类，但是k的选取会影响聚类效果。

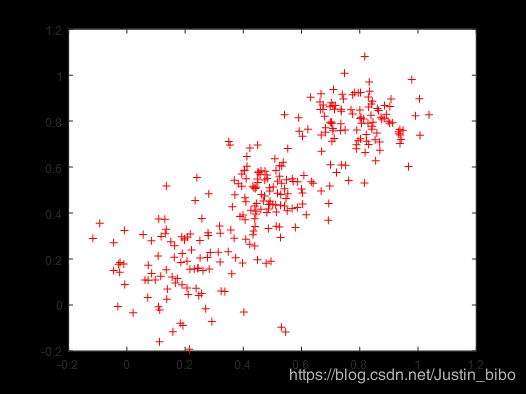
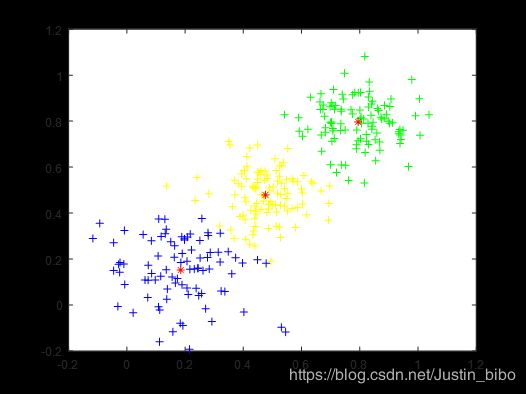
聚类效果

初始数据集

聚类之后，红色*是聚类中心

代码

function kmeans()
clear all;
clc;
k=3;%k为聚类个数
x = 0.8 + sqrt(0.01) * randn(100,2); %随机生成数据集
y = 0.2 + sqrt(0.02) * randn(100,2);
z= 0.5 + sqrt(0.01) * randn(100,2);
%  plot(x(:,1),x(:,2),'+r',y(:,1),y(:,2),'+b',z(:,1),z(:,2),'+g');
% axis([0,1,0,1]);xlabel('red');ylabel('acc');title('');
D=[x;y;z]; %得到数据集
% plot(D(:,1),D(:,2),'+r'); %可查看初始数据集的分布
u=randperm(size(D,1),k);%随机选k个向量作为初始向量
u=D(u,:);
c=zeros(size(D,1),1);%存放聚类标签
distance=zeros(k,1);%存放样本与均值向量的距离。
while 1 %循环开始
    mark=0;%标记是否有均值向量更新
    for i=1:size(D,1)
        for j=1:k
            distance(j)=sqrt((D(i,1)-u(j,1))^2+(D(i,2)-u(j,2))^2);%计算样本与均值向量的距离
        end
        [~,m]=min(distance);
        c(i)=m;     %把样本的划分到距离最近的簇
    end
    u1=zeros(k,2); %新的均值向量
    for i=1:k
        u1(i,1)=sum(D(find(c(:)==i),1))/size(find(c(:)==i),1);%计算新的均值向量
        u1(i,2)=sum(D(find(c(:)==i),2))/size(find(c(:)==i),1);%计算新的均值向量
        if u(i,1)~=u1(i,1)||u(i,2)~=u1(i,2)
            mark=1;
            u(i,1)=u1(i,1);%更新均值向量u
            u(i,2)=u1(i,2);
        end
    end
   if mark==0
       break;
   end
end
x=D(find(c(:)==1),:); %根据簇标签来分类，不同的类别用不同的颜色
y=D(find(c(:)==2),:);
z=D(find(c(:)==3),:);
 plot(x(:,1),x(:,2),'+y',y(:,1),y(:,2),'+b',z(:,1),z(:,2),'+g',u(1,1),u(1,2),'*r',u(2,1),u(2,2),'*r',u(3,1),u(3,2),'*r');
axis([0,1,0,1]);xlabel('red');ylabel('acc');title('');
end