目录
- 一、二叉树的遍历
- 1.1 先序遍历
- 1.2 中序遍历
- 1.3 后序遍历
- 1.4 小结
- 二、二叉树的非递归遍历
- 2.1 中序遍历非递归遍历算法
- 2.2 先序遍历的非递归遍历算法
- 2.3 后序遍历的非递归遍历算法
- 三、层序遍历
- 3.1 队列实现
- 四、实际应用
- 4.1 遍历二叉树的应用:输出二叉树中的叶子节点
- 4.2 求二叉树的高度
- 4.3 二元运算表达式树及其遍历
- 4.4 由两种遍历序列确定二叉树
一、二叉树的遍历
1.1 先序遍历
遍历过程为:
- 访问根结点
- 先序遍历其左子树;
- 先序遍历其右子树。
/* c语言实现 */
// 定义结点
typedef struct TreeNode *BinTree;
typedef BinTree Position;
struct TreeNode{
ElementType Data;
BinTree Left;
BinTree Right;
}
void PreOrderTraversal (BinTree BT)
{
if (BT) {
printf("%d", BT->Data);
PreOrderTraversal(BT->Left);
PreOrderTraversal(BT->Right);
}
}# python语言实现
# 定义结点
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def preorder(root):
if not root:
return
print(root.val)
preorder(root.left)
preorder(root.right) 先序遍历:A (B D F E)(C G H I)
1.2 中序遍历
遍历过程为:
- 中序遍历其左子树;
- 访问根节点;
- 中序遍历其右子树。
/* c语言实现 */
void InOrderTraversal (BinTree BT)
{
if (BT) {
InOrderTraversal(BT->Left);
printf("%d", BT->Data);
InOrderTracersal(BT->Right);
}
}# python语言实现
def inorder(root):
if not root:
return
inorder(root.left)
print(root.val)
inorder(root.right)中序遍历:(D B E F)A(G H C I)
1.3 后序遍历
遍历过程为:
- 后序遍历其左子树;
- 后序遍历其右子树;
- 访问根结点。
/* c语言实现 */
void PostOrderTraversal (BinTree BT)
{
if (BT) {
PostOrderTraversal(BT->Left);
PostORderTraversal(BT->Right);
printf("%d", BT->Data);
}
}# python语言实现
def postorder(root):
if not root:
return
postorder(root.left)
postorder(root.right)
print(root.val)后序遍历:(D E F B)(H G I C)A
1.4 小结
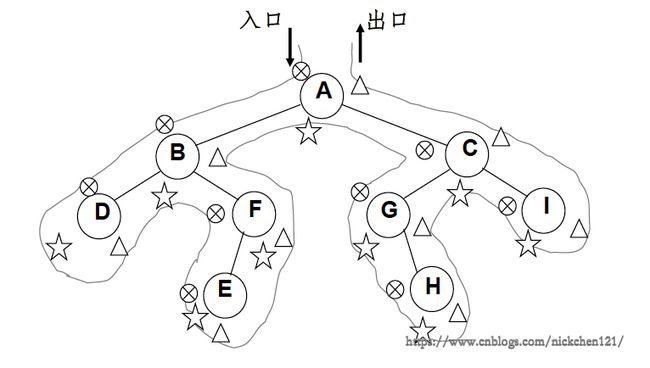
先序、中序和后序遍历过程:遍历过程中经过结点的路线一样,只是访问各结点的时机不同。
图中在从入口到出口的曲线上用×、☆、△三种符号分别标记出了先序、中序和后序访问各结点的时刻。
二、二叉树的非递归遍历
非递归算法实现的基本思路:使用堆栈
2.1 中序遍历非递归遍历算法
- 遇到一个结点,就把它压栈,并去遍历它的左子树;
- 当左子树遍历结束后,从栈顶弹出这个结点并访问它;
- 然后按其右指针再去中序遍历该结点的右子树。
/* c语言实现 */
void InOrderTraversal(BinTree BT)
{
BinTree T = BT;
Stack S = CreateStack(MaxSize); // 创建并初始化堆栈S
while (T || !IsEmpty(S)){
while (T) { // 一直向左并将沿途结点压入堆栈
Push(S, T);
T = T->Left;
}
if (!IsEmpty(S)){
T = Pop(S); // 结点弹出堆栈
printf("%5d", T->Data); // (访问)打印结点
T = T->Right; // 转向右子树
}
}
}# python语言实现
def inorder(root):
stack = []
while stack or root:
while root:
stack.append(root)
root = root.left
root = stack.pop()
print(root.val)
root = root.right2.2 先序遍历的非递归遍历算法
/* c语言实现 */
void InOrderTraversal(BinTree BT)
{
BinTree T = BT;
Stack S = CreateStack(MaxSize); // 创建并初始化堆栈S
while (T || !IsEmpty(s)){
while (T) { // 一直向左并将沿途结点压入堆栈
printf("%5d", T->Data); // (访问)打印结点
Push(S, T);
T = T->Left;
}
if (!IsEmpty(S)){
T = Pop(S); // 结点弹出堆栈
T = T->Right; // 转向右子树
}
}
}# python语言实现
def preorder(root):
stack = [root]
while stack:
s = stack.pop()
if s:
print(s.val)
stack.append(s.right)
stack.append(s.left)2.3 后序遍历的非递归遍历算法
// c语言实现
// 定义结点
typedef struct TreeNode{
int data;
struct TreeNode *lChild;
struct TreeNode *rChild;
} TreeNode;
void postOrder(TreeNode *T){
TreeNode *stack[15];
int top = -1;
int flagStack[15]; //记录每个节点访问次数栈
TreeNode *p = T;
while(p!=NULL||top!=-1){
if(p!=NULL){ //第一次访问,flag置1,入栈
stack[++ top] = p;
flagStack[top] = 1;
p = p->lChild;
}else{//(p == NULL)
if(flagStack[top] == 1){ //第二次访问,flag置2,取栈顶元素但不出栈
p = stack[top];
flagStack[top] = 2;
p = p->rChild;
}else{ //第三次访问,出栈
p = stack[top --];
printf("%d\t",p->data); //出栈时,访问输出
p = NULL; //p置空,以便继续退栈
}
}
}# python语言实现
def postorder(root):
stack = []
while stack or root:
while root: # 下行循环,直到找到第一个叶子节点
stack.append(root)
if root.left: # 能左就左,不能左就右
root = root.left
else:
root = root.right
s = stack.pop()
print(s.val)
#如果当前节点是上一节点的左子节点,则遍历右子节点
if stack and s == stack[-1].left:
root = stack[-1].right
else:
root = None三、层序遍历
二叉树遍历的核心问题:二维结构的线性化。即从结点访问其左、右儿子结点,访问左儿子后,如果根结点信息丢失,右儿子结点也会随之丢失,因此需要一个存储结构保存暂时不访问的结点,这个存储结构可以为堆栈,也可以是队列。
3.1 队列实现
遍历从根节点开始,首先将根节点入队,然后开始执行循环:结点出队、访问该结点、其左右儿子入队。
层序基本过程:先根结点入队,然后:
- 从队列中取出一个元素;
- 访问该元素所指结点;
- 若该元素所指结点的左、右孩子结点非空,则将其左、右孩子的指针顺序入队。
/* c语言实现 */
void LevelOrderTraversal (BinTree BT)
{
Queue Q; BinTree T;
if (!BT) return; // 若是空树则直接返回
Q = CreateQueue(MaxSize); // 创建并初始化队列Q
AddQ(Q, BT);
while (!IsEmptyQ(Q))
{
T = DeleteQ(Q);
printf("%d\n", T->Data); // 访问取出队列的结点
if (T->Left) AddQ(Q, T->Left);
if (T->Right) AddQ(Q, T->Right);
}
}# python语言实现
def BFS(root):
queue = [root]
while queue:
n = len(queue)
for i in range(n):
q = queue.pop(0)
if q:
print(q.val)
queue.append(q.left if q.left else None)
queue.append(q.right if q.right else None)四、实际应用
4.1 遍历二叉树的应用:输出二叉树中的叶子节点
在二叉树的遍历算法中检测结点的左右子树是否都为空。
/* c语言实现 */
void PreOrderPrintLeaves (BinTree BT)
{
if (BT) {
if (!BT->Left && !BT->Right)
printf("%d", BT->Data);
PreOrderPrintLeaves(BT->Left);
PreOrderPrintLeaves(BT->Right);
}
}# python语言实现
class Node(object):
"""节点类"""
def __init__(self, val=-1, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Tree(object):
"""树类"""
def __init__(self):
self.root = Node()
self.queue = [] # 使用列表模拟队列
def add(self, val):
"""为树添加节点"""
node = Node(val)
if self.root.val == -1: # 如果树是空的,则对根节点赋值
self.root = node
self.queue.append(self.root)
else:
treeNode = self.queue[0] # 此结点的子树还没有齐。
if treeNode.left == None:
treeNode.left = node # 左子树变成节点(初始此节点左右都是None)
self.queue.append(treeNode.left)
else:
treeNode.right = node
self.queue.append(treeNode.right)
self.queue.pop(0) # 如果该结点存在右子树,将此结点丢弃。
def leave(self, root):
if root == None:
return 0
elif root.left == None and root.right == None:
return 1
else:
return (self.leave(root.left) + self.leave(root.right)) # 递归遍历所有左子树右子树,当左右都为None时才算1
if __name__ == '__main__':
"""主函数"""
vals = range(10) # 生成十个数据作为树节点
tree = Tree() # 新建一个树对象
for val in vals:
tree.add(val) # 逐个添加树的节点
print('叶子节点个数:', tree.leave(tree.root))4.2 求二叉树的高度
/* c语言实现 */
int PostOrderGetHeight(BinTree BT)
{
int HL, HR, MaxH;
if (BT) {
HL = PostOrderGetHeight(BT->Left); // 求左子树的深度
HR = PostOrderGetHeight(BT->Right); // 求右子树的深度
MaxH = (HL > HR) ? HL : HR; // 取左右子树较大的深度
return (MaxH + 1); // 返回树的深度
}
else return 0; // 空树深度为0
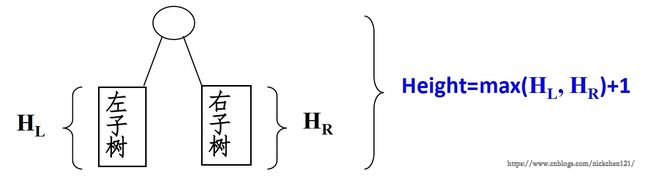
}# python实现
# 基本思路就是递归,当前树的最大深度等于(1+max(左子树最大深度,右子树最大深度))。
def maxDepth(root):
if not root:
return 0
return 1+max(maxDepth(root.left), maxDepth(root.right))4.3 二元运算表达式树及其遍历
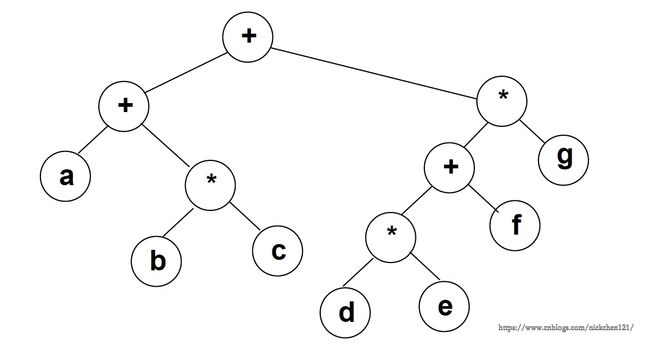
- 先序遍历得到前缀表达式:
++a*bc*+*defg - 中序遍历得到中缀表达式(中缀表达式会受到运算符优先级的影响):
a+b*c+d*e+f*g - 后序遍历得到后缀表达式:
abc*+de*f+g*+
4.4 由两种遍历序列确定二叉树
已知三种遍历中的任意两种遍历序列,不能唯一确定一颗二叉树,如果两种遍历序列中有中序遍历,则可以唯一确定一颗二叉树。
对于给出的先序遍历序列为:AB和后序遍历序列:BA,可能有如下两种情况:
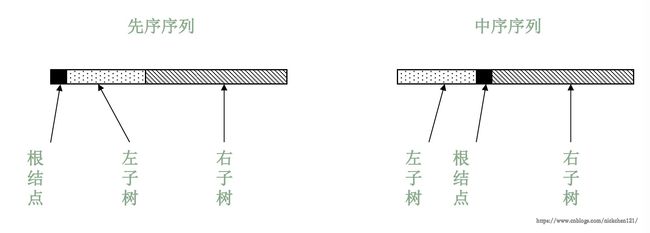
先序和中序遍历序列来确定一颗二叉树
- 根据先序遍历序列第一个结点确定根节点
- 根据根节点在中序遍历序列中分割出左右两个子序列
- 对左子树和右子树分别递归使用相同的方法继续分解
类似地,后序和中序遍历序列也可以确定一颗二叉树。