R语言入门(2)时间序列分析原理
1、随机游走模型
1.1 基本介绍
随机游走模型是时间序列分析中最基本的概念,是一个著名的非平稳序列。公式如下:
式中, ut 是一个随机误差,我们通常假设它服从(0,1)的正态分布。根据公式,我们可以推导得出,随机游走模型的均值 E(Yt) 是一个常量0,不随时间变化,而方差 Var(Yt)=t×Var(u) ,随时间变化,这就说明该随机游走模型是非平稳的。很简单,这里不作推导了。
可以用R来生成一个服从随机游走模型的时间序列,代码如下:
(1)首先参考这篇博客用R生成一组随机数据的方法,具体方法如下:
# 常用随机数字
runif(n,min=0,max=1) #uniform,均匀分布
rnorm(n,mean=0,sd=1) #Gaussian(normal),正态分布
rexp(n,rate=1) #exponential,指数分布
rlnorm(n,meanlog=0,sdlog=1) #lognormal,对数正态分布 (2)然后一列全为0的数组,循环计算出每一个点,得到时间序列。最后对时间序列作平稳性检验。
x <- matrix(0, 1000, 1)
for (i in 1:1000) {
x[i+1] <- x[i] + rnorm(1)
}
plot(x, type = "l")
library(tseries)
adf.test(x)1.2 衍生模型-AR(1)模型
我们在随机模型的基础上增加一个系数a,来看看时间序列是否平稳。其实这就是 AR(1) 模型,也就是说随机游走模型是AR(1)模型的特例。
(1)当 a=0 时,时间序列如下图所示
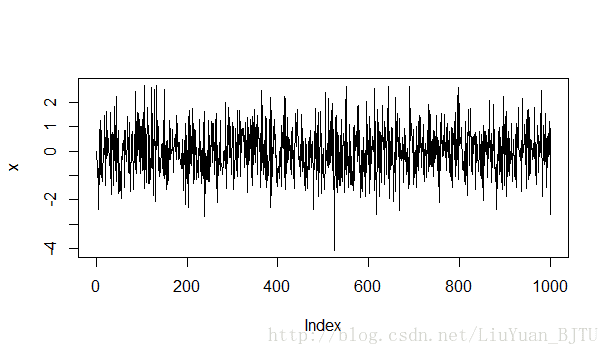
平稳性检验结果如下。p值小于0.05,在0.05的置信水平下,拒绝原假设,选择备择假设:该时间序列平稳。
> adf.test(x)
Augmented Dickey-Fuller Test
data: x
Dickey-Fuller = -9.8862, Lag order = 9, p-value = 0.01
alternative hypothesis: stationary(2)当 a=0.5 时,时间序列如下图所示

平稳性检验结果如下。p值小于0.05,在0.05的置信水平下,拒绝原假设,选择备择假设:该时间序列平稳。
> adf.test(x)
Augmented Dickey-Fuller Test
data: x
Dickey-Fuller = -9.5753, Lag order = 9, p-value = 0.01
alternative hypothesis: stationary(3)当 a=0.9 时,时间序列如下图所示
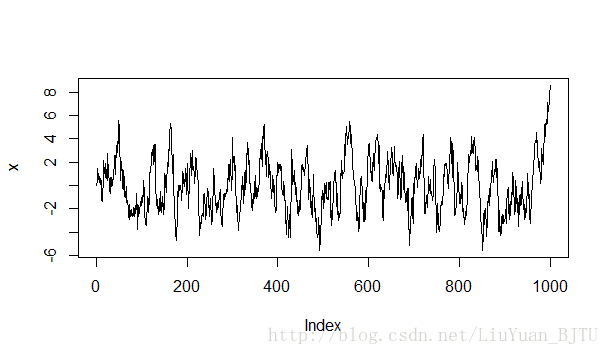
平稳性检验结果如下。p值小于0.05,在0.05的置信水平下,拒绝原假设,选择备择假设:该时间序列平稳。
> adf.test(x)
Augmented Dickey-Fuller Test
data: x
Dickey-Fuller = -6.4184, Lag order = 9, p-value = 0.01
alternative hypothesis: stationary(4)当 a=1.1 时,时间序列如下图所示
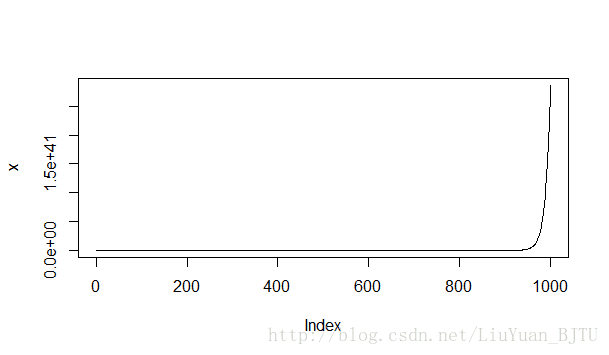
很显然,该时间序列是非平稳序列。
综上所述,对于模型 Yt=a∗Yt−1+ut 而言:
当 0<a<1 时,该模型是平稳序列。
当 a>=1 时,该模型是非平稳序列。
从公式上来理解就是,
For instance, if X(t – 1 ) = 1, E[X(t)] = 0.5 ( for a = 0.5) . Now, if X moves to any direction from zero, it is pulled back to zero in next step. The only component which can drive it even further is the error term. Error term is equally probable to go in either direction. What happens when the Rho becomes 1? No force can pull the X down in the next step.
具体可以看这篇国外博客
1.3 ADF单位根平稳型检验原理
首先对公式进行变形,把
然后对 (a−1) 进行假设检验,原假设为: a−1=0 ,备择假设为: a−1!=0 ,如果p值小于0.05,拒绝原假设,就说明该时间序列是平稳的。
2、最小二乘法
2.1 最小二乘法原理
最小二乘法 (Ordinary Least Square,OLS),又称为最小平方法,是一种参数估计方法,通常用于连续变量的回归分析。
下面以一元线性回归模型的最小二乘法进行说明。假设给定了 n 个数据对 (x1,y1),(x2,y2),,,(xn,yn) ,要求变量X与Y之间的关系。我们假设两个变量之间是线性关系,即变量Y是变量X的线性函数,因此可以得到一元线性回归模型,如下所示:
式中, e 称为残差(residual),即拟合值与实际值的差值,从几何的角度来理解,就是所有散点与拟合直线的欧式距离。
最小二乘法:要找到一组 β1 与 β2 使残差的平方和最小,即:
得到的函数 S(β1,β2) 是一个关于 β1 、 β2 的二元二次函数。
进一步,如果在 n+1 维空间中有 m 个数据点,数据点为 (x1,x2,...,xn,y) ,就可以多元线性函数来拟合因变量 Y 与自变量 X1,X2,...,Xn 之间的关系。具体见 维基百科-最小二乘法
拟合函数为:
目标函数为:
同样可以用矩阵的形式来推导出向量 β^ 的值
拟合函数为:
目标函数为
要使误差 S(β) 最小, β^ 要满足正规方程(normal equation),即向量 x1,x2,...,xm 与误差向量 y1−x1β^,y2−x2β^,...,ym−xmβ^ 垂直。具体推导过程见 掰开揉碎推导Normal Equation-知乎专栏
转换一下就是:
其中, XTX 是矩阵X的格拉姆矩阵(Gramian matrix),具有半正定性。 XTy 是矩阵X的矩矩阵,如协方差矩阵。
所以参数 β^ 为:
2.2 R语言实现最小二乘法
用R语言实现最小二乘法的代码如下:
m <- 4
n <- 2
input <- matrix(c(1, 6, 2, 5, 3, 7, 4, 10), ncol = n, byrow = T)
k <- rep(1,m)
X <- cbind(k, input[,1])
y <- input[,2]
X.T <- t(X)
betaHat <- solve(X.T%*%X) %*% X.T %*%y
print(betaHat)
plot(input)
abline(betaHat[1], betaHat[2])2.3引申:求解二次多元函数最优化问题
由于目标函数 S(β) 是一个二次多元函数的优化问题,因此可以用梯度下降法(Gradient Descent)来求解。
梯度下降法是一种数值求解算法,具有以下特点
(1)需要预先选定Learning rate(步长);
(2)需要多次iteration;
(3)需要Feature Scaling(特征缩放、降维);
最小二乘法中的正规方程(Normal Equation)是一种投影方法,具有简单、方便特点,且不需要Feature Scaling。该方法也有使用限制:当等式数量(样本量)远远大于未知数(维度)的数量时,即 m>>n 时,就不能使用Normal Equation。
3、AR过程和MA过程
举个例子来说明AR过程与MA过程
4、概率论与统计学相关知识
平稳时间序列的自协方差函数
在概率论和统计学中,数学期望(mean)是试验中每次可能结果的概率乘以其结果的总和,即该变量输出值的平均值: E(Yt)=mean(Yt)
由于在平稳时间序列的均值和方差在任何时刻不发生变化,所以 E(Yt+k)=E(Yt) ,进而可以把自协方差函数写作:
平稳时间序列的自相关函数ACF
方差(variance)是用来衡量随机变量或一组数据时离散程度的度量,即用来度量随机变量和其数学期望(即均值)之间的偏离程度。
var(X)=D(X)=E[X−E(X)]2
该公式的含义是:每一时刻“X值与其均值的差”平方后得到一个数值,再将每个时刻的该数值求平均。【标准差后面还有开方】协方差(covariance)用于衡量两个变量在变化过程中是同方向变化,还是反方向变化(根据正负来判断,同向为正,反向为负),程度如何(根据数值大小来判断)?
cov(X,Y)=E[X−E(X)][Y−E(Y)]
该公式的含义是:每个时刻“X值与其均值的差”乘以“Y值与其均值的差”得到一个乘积,在对每个时刻该乘积求和并求出均值。相关系数(correlation)看作剔除了两个变量量纲影响、标准化后的特殊协方差。
因为变量X与变量Y的量纲可能不同,比如 X=sin(t) Y=10000sin(t) ,变量X在0到1之间波动,Y在0到10000之间波动,两者幅度不同,但是变化过程具有极高的相似度。但是计算出来的协方差约为1.5,很小不足以反映两个变量之间的相关程度。所以要通过除以标准差的方式来剔除变化幅度的影响。
α(X,Y)=cov(X,Y)var(X)var(Y)√具体的理解可以参考知乎上的GRAYLAMB的回答:如何通俗易懂地解释「协方差」与「相关系数」的概念?
平稳时间序列的偏自相关函数PACF
对于一个平稳AR(p)模型,求出滞后k自相关系数 p(k) 时,实际上得到并不是 Yt 与 Yt+k 之间单纯的相关关系。因为 Yt 同时还会受到中间 k−1 个随机变量 Yt+1、Yt+2、……、Yt+k−1 的影响,而这k-1个随机变量又都和 Yt+k 具有相关关系,所以自相关系数 p(k) 里实际掺杂了其他变量对 Yt 与 Yt+k 的影响。
对于平稳时间序列 Yt ,所谓滞后k偏自相关系数指在给定中间 k−1 个随机变量 Yt+1、Yt+2、……、Yt+k−1 的条件下,或者说,在剔除了中间 k−1 个随机变量 Yt+1、Yt+2、……、Yt+k−1 的干扰之后, Yt+k 对 Yt 影响的相关程度。
其公式如下:
式中, Pt,k(Yt) 是指 Yt 在由 Yt+1、Yt+2、……、Yt+k−1 构成的空间中的投影。