[数学理论]Cross-Validation(交叉验证)介绍
转载于https://zhuanlan.zhihu.com/p/24825503?refer=rdatamining
在机器学习里,通常来说我们不能将全部用于数据训练模型,否则我们将没有数据集对该模型进行验证,从而评估我们的模型的预测效果。为了解决这一问题,有如下常用的方法:
1.The Validation Set Approach
第一种是最简单的,也是很容易就想到的。我们可以把整个数据集分成两部分,一部分用于训练,一部分用于验证,这也就是我们经常提到的训练集(training set)和测试集(test set)。
例如,如上图所示,我们可以将蓝色部分的数据作为训练集(包含7、22、13等数据),将右侧的数据作为测试集(包含91等),这样通过在蓝色的训练集上训练模型,在测试集上观察不同模型不同参数对应的MSE的大小,就可以合适选择模型和参数了。
不过,这个简单的方法存在两个弊端。
1.最终模型与参数的选取将极大程度依赖于你对训练集和测试集的划分方法。什么意思呢?我们再看一张图:
<img src="https://pic1.zhimg.com/v2-577bb114a1073273452cc1c73045e274_b.png" data-rawwidth="1027" data-rawheight="409" class="origin_image zh-lightbox-thumb" width="1027" data-original="https://pic1.zhimg.com/v2-577bb114a1073273452cc1c73045e274_r.png">右边是十种不同的训练集和测试集划分方法得到的test MSE,可以看到,在不同的划分方法下,test MSE的变动是很大的,而且对应的最优degree也不一样。所以如果我们的训练集和测试集的划分方法不够好,很有可能无法选择到最好的模型与参数。
右边是十种不同的训练集和测试集划分方法得到的test MSE,可以看到,在不同的划分方法下,test MSE的变动是很大的,而且对应的最优degree也不一样。所以如果我们的训练集和测试集的划分方法不够好,很有可能无法选择到最好的模型与参数。
2.该方法只用了部分数据进行模型的训练
我们都知道,当用于模型训练的数据量越大时,训练出来的模型通常效果会越好。所以训练集和测试集的划分意味着我们无法充分利用我们手头已有的数据,所以得到的模型效果也会受到一定的影响。
基于这样的背景,有人就提出了Cross-Validation方法,也就是交叉验证。
2.Cross-Validation
2.1 LOOCV
首先,我们先介绍LOOCV方法,即(Leave-one-out cross-validation)。像Test set approach一样,LOOCV方法也包含将数据集分为训练集和测试集这一步骤。但是不同的是,我们现在只用一个数据作为测试集,其他的数据都作为训练集,并将此步骤重复N次(N为数据集的数据数量)。
<img src="https://pic1.zhimg.com/v2-27f8c5989dd7790ccf6b626e6854e06c_b.png" data-rawwidth="820" data-rawheight="450" class="origin_image zh-lightbox-thumb" width="820" data-original="https://pic1.zhimg.com/v2-27f8c5989dd7790ccf6b626e6854e06c_r.png">如上图所示,假设我们现在有n个数据组成的数据集,那么LOOCV的方法就是每次取出一个数据作为测试集的唯一元素,而其他n-1个数据都作为训练集用于训练模型和调参。结果就是我们最终训练了n个模型,每次都能得到一个MSE。而计算最终test MSE则就是将这n个MSE取平均。
如上图所示,假设我们现在有n个数据组成的数据集,那么LOOCV的方法就是每次取出一个数据作为测试集的唯一元素,而其他n-1个数据都作为训练集用于训练模型和调参。结果就是我们最终训练了n个模型,每次都能得到一个MSE。而计算最终test MSE则就是将这n个MSE取平均。
<img src="https://pic1.zhimg.com/v2-c6a79e230f946da8aefd793ed57c0454_b.png" data-rawwidth="340" data-rawheight="136" class="content_image" width="340">
比起test set approach,LOOCV有很多优点。首先它不受测试集合训练集划分方法的影响,因为每一个数据都单独的做过测试集。同时,其用了n-1个数据训练模型,也几乎用到了所有的数据,保证了模型的bias更小。不过LOOCV的缺点也很明显,那就是计算量过于大,是test set approach耗时的n-1倍。
为了解决计算成本太大的弊端,又有人提供了下面的式子,使得LOOCV计算成本和只训练一个模型一样快。
<img src="https://pic2.zhimg.com/v2-ec72b82d605902ddfa060c2fb5777a05_b.png" data-rawwidth="383" data-rawheight="123" class="content_image" width="383">其中
其中表示第i个拟合值,而则表示leverage。
2.2 K-fold Cross Validation
另外一种折中的办法叫做K折交叉验证,和LOOCV的不同在于,我们每次的测试集将不再只包含一个数据,而是多个,具体数目将根据K的选取决定。比如,如果K=5,那么我们利用五折交叉验证的步骤就是:
1.将所有数据集分成5份
2.不重复地每次取其中一份做测试集,用其他四份做训练集训练模型,之后计算该模型在测试集上的MSEi
3.将5次的MSEi取平均得到最后的MSE
<img src="https://pic4.zhimg.com/v2-fcb843dd06c15a515d03a543864bbb77_b.png" data-rawwidth="314" data-rawheight="97" class="content_image" width="314">不难理解,其实LOOCV是一种特殊的K-fold Cross Validation(K=N)。再来看一组图:
不难理解,其实LOOCV是一种特殊的K-fold Cross Validation(K=N)。再来看一组图:
<img src="https://pic2.zhimg.com/v2-daf077823e7faa57c6f4014389fe12b9_b.png" data-rawwidth="1011" data-rawheight="426" class="origin_image zh-lightbox-thumb" width="1011" data-original="https://pic2.zhimg.com/v2-daf077823e7faa57c6f4014389fe12b9_r.png">每一幅图种蓝色表示的真实的test MSE,而黑色虚线和橙线则分贝表示的是LOOCV方法和10-fold CV方法得到的test MSE。我们可以看到事实上LOOCV和10-fold CV对test MSE的估计是很相似的,但是相比LOOCV,10-fold CV的计算成本却小了很多,耗时更少。
每一幅图种蓝色表示的真实的test MSE,而黑色虚线和橙线则分贝表示的是LOOCV方法和10-fold CV方法得到的test MSE。我们可以看到事实上LOOCV和10-fold CV对test MSE的估计是很相似的,但是相比LOOCV,10-fold CV的计算成本却小了很多,耗时更少。
2.3 Bias-Variance Trade-Off for k-Fold Cross-Validation
最后,我们要说说K的选取。事实上,和开头给出的文章里的部分内容一样,K的选取是一个Bias和Variance的trade-off。
K越大,每次投入的训练集的数据越多,模型的Bias越小。但是K越大,又意味着每一次选取的训练集之前的相关性越大(考虑最极端的例子,当k=N,也就是在LOOCV里,每次都训练数据几乎是一样的)。而这种大相关性会导致最终的test error具有更大的Variance。
一般来说,根据经验我们一般选择k=5或10。
2.4 Cross-Validation on Classification Problems
上面我们讲的都是回归问题,所以用MSE来衡量test error。如果是分类问题,那么我们可以用以下式子来衡量Cross-Validation的test error:
<img src="https://pic3.zhimg.com/v2-7302b5c15dcfc6746b51830b65debf62_b.png" data-rawwidth="284" data-rawheight="103" class="content_image" width="284">其中Erri表示的是第i个模型在第i组测试集上的分类错误的个数。
其中Erri表示的是第i个模型在第i组测试集上的分类错误的个数。
图片来源:《An Introduction to Statistical Learning with Applications in R》
![[数学理论]Cross-Validation(交叉验证)介绍_第1张图片](http://img.e-com-net.com/image/info8/d104afebd13e4b558909c36adc4e7544.jpg)
![[数学理论]Cross-Validation(交叉验证)介绍_第2张图片](http://img.e-com-net.com/image/info8/8e6b01fde37f43c7a845e9a9039b4d2f.jpg)
![[数学理论]Cross-Validation(交叉验证)介绍_第3张图片](http://img.e-com-net.com/image/info8/984f1c06bc60482aa3148665c6669a5f.png)
![[数学理论]Cross-Validation(交叉验证)介绍_第4张图片](http://img.e-com-net.com/image/info8/74868e732eaa4983833369e510af92ca.jpg)
![[数学理论]Cross-Validation(交叉验证)介绍_第5张图片](http://img.e-com-net.com/image/info8/955d4ee11bea4dc1a8a22ae09b53765b.jpg)
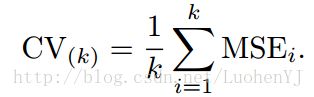
![[数学理论]Cross-Validation(交叉验证)介绍_第6张图片](http://img.e-com-net.com/image/info8/02d0745afd73448a938e91018ad3ea88.jpg)
![[数学理论]Cross-Validation(交叉验证)介绍_第7张图片](http://img.e-com-net.com/image/info8/4a0b7522e1204d25a484654ca47ec16c.jpg)