【机器学习】RBF神经网络原理与Python实现

一、RBF神经网络原理

1. RBF神经网络结构与RBF神经元

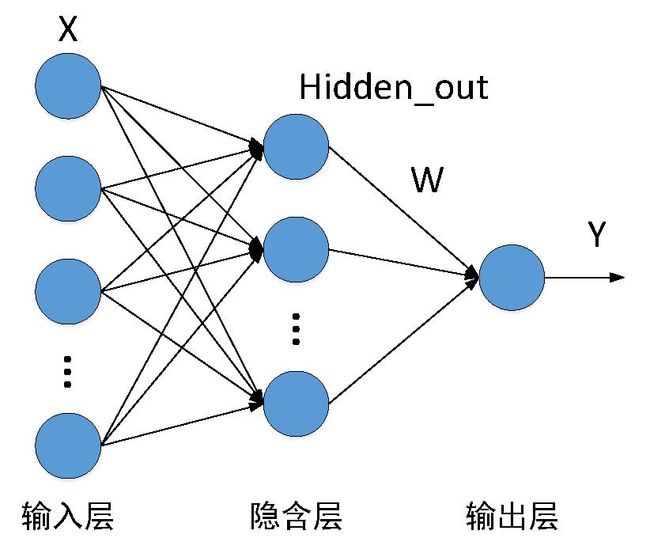
RBF神经网络的结构图如上图所示，其结构与简单的BP神经网络相同都是三层网络结构：输入层、隐含层和输出层。不同的是，RBF神经网络的隐含层节点的激活函数为径向基（RBF）函数。
假设训练数据集为$X=\left\{x^1,x^2,\cdots ,x^m\right\}$，其中第i个训练样本为$x^i=\left\{x_1^i,x_2^i,\cdots ,x_n^i\right\}$，也就是说样本数为m，特征数为n，所以输入层的节点个数为n。假设隐含层节点个数为s，第i个训练样本$x^i$从隐含层的第j个节点（$j=1,2,\cdots ,s$）的输出为：

$G\left(x^i,c^j\right)=\exp \left(-\frac{1}{2{\left({\sigma }^j\right)}^2}\Vert x^i-c^j\Vert \right)$

其中$c^j$和${\sigma }^j$分别是RBF神经网络第j个隐含层RBF激活函数的中心参数和宽度参数【参考资料1】。
隐含层输出通过权重矩阵映射到输出层的输入，本博文中输出层节点的激励函数为线性函数（$y=x$）。

RBF神经网络的数据流向为：训练样本—RBF隐含层—权重矩阵—输出层

2. RBF神经网络求解

RBF神经网络是BP神经网络的特殊形式，因此求解过程也与BP神经网络相同，分为两个部分：正向传播计算误差和反向传播调整参数。

2.1 正向传播：计算误差

对于样本$x^i$，RBF神经网络的输出为$y^i$：

${\hat{y}}^i=\sum _{j=1}^s{w}_{j}G\left(x^i,c^j\right)$

样本标签为$\left\{y^1,y^2,\cdots ,y^m\right\}$，RBF神经网络的损失函数为:

$Loss=\frac{1}{2}\sum _{i=1}^m{e_i}^2=\frac{1}{2}\sum _{i=1}^m{\left(y^i-{\hat{y}}^i\right)}^2=\frac{1}{2}\sum _{i=1}^m{\left(y^i-\sum _{j=1}^s{w}_{j}G\left(x^i,c^j\right)\right)}^2$

2.2 反向传播：调整参数

利用梯度下降法迭代求取$\left\{c^1,c^2,\cdots ,c^j\right\}$、$\left\{{\sigma }^1,{\sigma }^2,\cdots ,{\sigma }^j\right\}$和$\left\{w_1,w_2,\cdots ,w_j\right\}$【参考资料2】。

$c^j=c^j-\alpha \frac{\partial Loss}{\partial c^j}$

${\sigma }^j={\sigma }^j-\alpha \frac{\partial Loss}{\partial {\sigma }^j}$

$w^j=w^j-\alpha \frac{\partial Loss}{\partial w^j}$
其求解过程为：
$\{\begin{array}{c}\Delta c^j=-\alpha \frac{\partial Loss}{\partial c^j}=\alpha \frac{w_j}{{\left({\sigma }^j\right)}^2}\sum _{i=1}^m{e}_{i}G\left(x^i,c^j\right)\left(x^i-c^j\right)\\ \Delta {\sigma }^j=-\alpha \frac{\partial Loss}{\partial {\sigma }^j}=\alpha \frac{w_j}{{\left({\sigma }^j\right)}^3}\sum _{i=1}^m{e}_{i}G\left(x^i,c^j\right){\Vert x^i-c^j\Vert }^2\\ \Delta w_j=-\alpha \frac{\partial Loss}{\partial w_j}=\alpha \sum _{i=1}^m{e}_{i}G\left(x^i,c^j\right)\end{array}$

二、RBF神经网络的python实现

代码及样本地址:https://github.com/shiluqiang/RBF_NN_Python
RBF神经网络模型训练：

// 
from numpy import *
from math import sqrt

def load_data(file_name):
    '''导入数据
    input:  file_name(string):文件的存储位置
    output: feature_data(mat):特征
            label_data(mat):标签
            n_class(int):类别的个数
    '''
    # 1、获取特征
    f = open(file_name)  # 打开文件
    feature_data = []
    label = []
    for line in f.readlines():
        feature_tmp = []
        lines = line.strip().split("\t")
        for i in range(len(lines) - 1):
            feature_tmp.append(float(lines[i]))
        label.append(int(lines[-1]))      
        feature_data.append(feature_tmp)
    f.close()  # 关闭文件
    n_output = 1
    
    return mat(feature_data), mat(label).transpose(), n_output

def linear(x):
    '''Sigmoid函数（输出层神经元激活函数）
    input:  x(mat/float):自变量，可以是矩阵或者是任意实数
    output: Sigmoid值(mat/float):Sigmoid函数的值
    '''
    return x
   

def hidden_out(feature,center,delta):
    '''rbf函数（隐含层神经元输出函数）
    input:feature(mat):数据特征
          center(mat):rbf函数中心
          delta(mat)：rbf函数扩展常数
    output：hidden_output（mat）隐含层输出
    '''
    m,n = shape(feature)
    m1,n1 = shape(center)
    hidden_out = mat(zeros((m,m1)))
    for i in range(m):
        for j in range(m1):
            hidden_out[i,j] = exp(-1.0 * (feature[i,:]-center[j,:]) * (feature[i,:]-center[j,:]).T/(2*delta[0,j]*delta[0,j]))        
    return hidden_out


def predict_in(hidden_out, w):
    '''计算输出层的输入
    input:  hidden_out(mat):隐含层的输出
            w1(mat):隐含层到输出层之间的权重
            b1(mat):隐含层到输出层之间的偏置
    output: predict_in(mat):输出层的输入
    '''
    m = shape(hidden_out)[0]
    predict_in = hidden_out * w
    return predict_in

    
def predict_out(predict_in):
    '''输出层的输出
    input:  predict_in(mat):输出层的输入
    output: result(mat):输出层的输出
    '''
    result = linear(predict_in)
    return result

def bp_train(feature, label, n_hidden, maxCycle, alpha, n_output):
    '''计算隐含层的输入
    input:  feature(mat):特征
            label(mat):标签
            n_hidden(int):隐含层的节点个数
            maxCycle(int):最大的迭代次数
            alpha(float):学习率
            n_output(int):输出层的节点个数
    output: center(mat):rbf函数中心
            delta(mat):rbf函数扩展常数
            w(mat):隐含层到输出层之间的权重
    '''
    m, n = shape(feature)
    # 1、初始化
    center = mat(random.rand(n_hidden,n))
    center = center * (8.0 * sqrt(6) / sqrt(n + n_hidden)) - mat(ones((n_hidden,n))) * (4.0 * sqrt(6) / sqrt(n + n_hidden))
    delta = mat(random.rand(1,n_hidden))
    delta = delta * (8.0 * sqrt(6) / sqrt(n + n_hidden)) - mat(ones((1,n_hidden))) * (4.0 * sqrt(6) / sqrt(n + n_hidden))   
    w = mat(random.rand(n_hidden, n_output))
    w = w * (8.0 * sqrt(6) / sqrt(n_hidden + n_output)) - mat(ones((n_hidden, n_output))) * (4.0 * sqrt(6) / sqrt(n_hidden + n_output))

    
    # 2、训练
    iter = 0
    while iter <= maxCycle:
        # 2.1、信号正向传播
        # 2.1.1、计算隐含层的输出
        hidden_output = hidden_out(feature,center,delta)
        # 2.1.3、计算输出层的输入
        output_in = predict_in(hidden_output, w)  
        # 2.1.4、计算输出层的输出
        output_out = predict_out(output_in)
        
        # 2.2、误差的反向传播
        error = mat(label - output_out)
        for j in range(n_hidden):
            sum1 = 0.0
            sum2 = 0.0
            sum3 = 0.0
            for i in range(m):
                sum1 += error[i,:] * exp(-1.0 * (feature[i]-center[j]) * (feature[i]-center[j]).T / (2 * delta[0,j]*delta[0,j])) * (feature[i] - center[j])
                sum2 += error[i,:] * exp(-1.0 * (feature[i]-center[j]) * (feature[i]-center[j]).T / (2 * delta[0,j]*delta[0,j])) * (feature[i] - center[j]) * (feature[i] - center[j]).T
                sum3 += error[i,:] * exp(-1.0 * (feature[i]-center[j]) * (feature[i]-center[j]).T / (2 * delta[0,j]*delta[0,j]))
            delta_center = (w[j,:]/(delta[0,j]*delta[0,j])) * sum1
            delta_delta = (w[j,:]/(delta[0,j]*delta[0,j]*delta[0,j])) * sum2
            delta_w = sum3
       # 2.3、 修正权重和rbf函数中心和扩展常数       
            center[j,:] = center[j,:] + alpha * delta_center
            delta[0,j] = delta[0,j] + alpha * delta_delta
            w[j,:] = w[j,:] + alpha * delta_w
        if iter % 10 == 0:
            cost = (1.0/2) * get_cost(get_predict(feature, center, delta, w) - label)
            print ("\t-------- iter: ", iter, " ,cost: ",  cost)
        if cost < 3:   ###如果损失函数值小于3则停止迭
            break               
        iter += 1           
    return center, delta, w

def get_cost(cost):
    '''计算当前损失函数的值
    input:  cost(mat):预测值与标签之间的差
    output: cost_sum / m (double):损失函数的值
    '''
    m,n = shape(cost)
    
    cost_sum = 0.0
    for i in range(m):
        for j in range(n):
            cost_sum += cost[i,j] * cost[i,j]
    return cost_sum / m

def get_predict(feature, center, delta, w):
    '''计算最终的预测
    input:  feature(mat):特征
            w0(mat):输入层到隐含层之间的权重
            b0(mat):输入层到隐含层之间的偏置
            w1(mat):隐含层到输出层之间的权重
            b1(mat):隐含层到输出层之间的偏置
    output: 预测值
    '''
    return predict_out(predict_in(hidden_out(feature,center,delta), w))

def save_model_result(center, delta, w, result):
    '''保存最终的模型
    input:  w0(mat):输入层到隐含层之间的权重
            b0(mat):输入层到隐含层之间的偏置
            w1(mat):隐含层到输出层之间的权重
            b1(mat):隐含层到输出层之间的偏置
    output: 
    '''
    def write_file(file_name, source):   
        f = open(file_name, "w")
        m, n = shape(source)
        for i in range(m):
            tmp = []
            for j in range(n):
                tmp.append(str(source[i, j]))
            f.write("\t".join(tmp) + "\n")
        f.close()
    
    write_file("center.txt", center)
    write_file("delta.txt", delta)
    write_file("weight.txt", w)
    write_file('train_result.txt',result)
    
def err_rate(label, pre):
    '''计算训练样本上的错误率
    input:  label(mat):训练样本的标签
            pre(mat):训练样本的预测值
    output: rate[0,0](float):错误率
    '''
    
    m = shape(label)[0]
    for j in range(m):
        if pre[j,0] > 0.5:
            pre[j,0] = 1.0
        else:
            pre[j,0] = 0.0

    err = 0.0
    for i in range(m):
        if float(label[i, 0]) != float(pre[i, 0]):
            err += 1
    rate = err / m
    return rate

if __name__ == "__main__":
    # 1、导入数据
    print ("--------- 1.load data ------------")
    feature, label, n_output = load_data("data.txt")
    # 2、训练网络模型
    print ("--------- 2.training ------------")
    center, delta, w = bp_train(feature, label, 20, 5000, 0.008, n_output)
    # 3、得到最终的预测结果
    print ("--------- 3.get prediction ------------")
    result = get_predict(feature, center, delta, w)    
    print ("训练准确性为：", (1 - err_rate(label, result)))
    # 4、保存最终的模型
    print ("--------- 4.save model and result ------------")
    save_model_result(center, delta, w, result)

RBF神经网络模型测试：

//
from numpy import * 
from RBF_TRAIN import get_predict

def load_data(file_name):
    '''导入数据
    input:  file_name(string):文件的存储位置
    output: feature_data(mat):特征
    '''
    f = open(file_name)  # 打开文件
    feature_data = []
    for line in f.readlines():
        feature_tmp = []
        lines = line.strip().split("\t")
        for i in range(len(lines)):
            feature_tmp.append(float(lines[i]))        
        feature_data.append(feature_tmp)
    f.close()  # 关闭文件
    return mat(feature_data)

def generate_data():
    '''在[-4.5,4.5]之间随机生成20000组点
    '''
    # 1、随机生成数据点
    data = mat(zeros((20000, 2)))
    m = shape(data)[0]
    x = mat(random.rand(20000, 2))
    for i in range(m):
        data[i, 0] = x[i, 0] * 9 - 4.5
        data[i, 1] = x[i, 1] * 9 - 4.5
    # 2、将数据点保存到文件“test_data”中
    f = open("test_data.txt", "w")
    m,n = shape(data)
    for i in range(m):
        tmp =[]
        for j in range(n):
            tmp.append(str(data[i,j]))
        f.write("\t".join(tmp) + "\n")
    f.close()       

def load_model(file_center, file_delta, file_w):
    
    def get_model(file_name):
        f = open(file_name)
        model = []
        for line in f.readlines():
            lines = line.strip().split("\t")
            model_tmp = []
            for x in lines:
                model_tmp.append(float(x.strip()))
            model.append(model_tmp)
        f.close()
        return mat(model)
    
    # 1、导入rbf函数中心
    center = get_model(file_center)
    
    # 2、导入rbf函数扩展常数
    delta = get_model(file_delta)
    
    # 3、导入隐含层到输出层之间的权重
    w = get_model(file_w)


    return center, delta, w

def save_predict(file_name, pre):
    '''保存最终的预测结果
    input:  pre(mat):最终的预测结果
    output:
    '''
    f = open(file_name, "w")
    m = shape(pre)[0]
    result = []
    for i in range(m):
        result.append(str(pre[i, 0]))
    f.write("\n".join(result))
    f.close()

if __name__ == "__main__":
    generate_data()
    # 1、导入测试数据
    print ("--------- 1.load data ------------")
    dataTest = load_data("test_data.txt")
    # 2、导入BP神经网络模型
    print ("--------- 2.load model ------------")
    center,delta,w = load_model("center.txt", "delta.txt", "weight.txt")
    # 3、得到最终的预测值
    print ("--------- 3.get prediction ------------")
    result = get_predict(dataTest, center, delta, w)
    # 4、保存最终的预测结果
    print ("--------- 4.save result ------------")
    save_predict("test_result.txt", result)

参考资料

【1】https://www.cnblogs.com/pinking/p/9349695.html
【2】https://www.cnblogs.com/zhangchaoyang/articles/2591663.html