【超参数寻优】量子粒子群算法（QPSO） 超参数寻优的python实现

一、粒子群算法的缺点

本人之前的博文（参考资料【1】）已经详细介绍了PSO算法，学习本博文前需要先学习PSO算法。

PSO算法的缺点：
1、需要设定的参数（惯性因子$w$，局部学习因子$c_1$和全局学习因子$c_2$）太多，不利于找到待优化模型的最优参数。
2、粒子位置变化缺少随机性，容易陷入局部最优的陷阱。

二、量子粒子群算法

量子粒子群优化（Quantum Particle Swarm Optimization，QPSO）算法取消了粒子的移动方向属性，粒子位置的更新跟该粒子之前的运动没有任何关系，这样就增加了粒子位置的随机性（参考资料【2】）。
量子粒子群算法中引入的新名词：
mbest：表示pbest的平均值，即平均的粒子历史最好位置。
量子粒子群算法的粒子更新步骤：
步骤一：计算mbest

$M_{best}=\frac{1}{M}\sum _{i=1}^M{p}_{best\_i}$

其中$M$表示粒子群的大小，$p_{best\_i}$表示当前迭代中的第$i$个$pbest$。

步骤二：粒子位置更新

$P_i=\varphi \cdot p_{best\_i}+(1-\varphi )gbest$

其中$gbest$表示当前全局最优粒子，$P_i$用于第$i$个粒子位置的更新。
粒子位置更新公式为：

$x_i=P_i\pm \alpha \left|M_{best}-x_i\right|\ln \left(\frac{1}{u}\right)$

其中$x_i$表示第$i$个粒子的位置，$\alpha$为创新参数，$\varphi$和$u$为$（0,1）$上的均匀分布数值。取$+$和$-$的概率为0.5。

由上所示，QPSO算法中只有一个创新参数$\alpha$设置，一般$\alpha$不大于1。

三、QPSO算法的python实现

完整python代码和样本地址：https://github.com/shiluqiang/QPSO_python
本博文以非线性SVM为待优化模型，待优化参数为正则化参数$C$和核参数 $\sigma$，适应度函数值为3-fold交叉验证平均值。

## 2. QPSO算法
class QPSO(object):
    def __init__(self,particle_num,particle_dim,alpha,iter_num,max_value,min_value):
        '''定义类参数
        particle_num(int):粒子群大小
        particle_dim(int):粒子维度，对应待寻优参数的个数
        alpha(float):控制系数
        iter_num(int):最大迭代次数
        max_value(float):参数的最大值
        min_value(float):参数的最小值
        '''
        self.particle_num = particle_num
        self.particle_dim = particle_dim
        self.iter_num = iter_num
        self.alpha = alpha
        self.max_value = max_value
        self.min_value = min_value

### 2.1 粒子群初始化
    def swarm_origin(self):
        '''初始化粒子群中的粒子位置
        input:self(object):QPSO类
        output:particle_loc(list):粒子群位置列表
        '''
        particle_loc = []
        for i in range(self.particle_num):
            tmp1 = []
            for j in range(self.particle_dim):
                a = random.random()
                tmp1.append(a * (self.max_value - self.min_value) + self.min_value)
            particle_loc.append(tmp1)
        
        return particle_loc

### 2.2 计算适应度函数数值列表
    def fitness(self,particle_loc):
        '''计算适应度函数值
        input:self(object):PSO类
              particle_loc(list):粒子群位置列表
        output:fitness_value(list):适应度函数值列表
        '''
        fitness_value = []
        ### 1.适应度函数为RBF_SVM的3_fold交叉校验平均值
        for i in range(self.particle_num):
            rbf_svm = svm.SVC(kernel = 'rbf', C = particle_loc[i][0], gamma = particle_loc[i][1])
            cv_scores = cross_validation.cross_val_score(rbf_svm,trainX,trainY,cv =3,scoring = 'accuracy')
            fitness_value.append(cv_scores.mean())
        ### 2. 当前粒子群最优适应度函数值和对应的参数
        current_fitness = 0.0
        current_parameter = []
        for i in range(self.particle_num):
            if current_fitness < fitness_value[i]:
                current_fitness = fitness_value[i]
                current_parameter = particle_loc[i]

        return fitness_value,current_fitness,current_parameter

### 2.3 粒子位置更新    
    def updata(self,particle_loc,gbest_parameter,pbest_parameters):
        '''粒子位置更新
        input:self(object):QPSO类
              particle_loc(list):粒子群位置列表
              gbest_parameter(list):全局最优参数
              pbest_parameters(list):每个粒子的历史最优值
        output:particle_loc(list):新的粒子群位置列表
        '''
        Pbest_list = pbest_parameters
        #### 2.3.1 计算mbest
        mbest = []
        total = []
        for l in range(self.particle_dim):
            total.append(0.0)
        total = np.array(total)
        
        for i in range(self.particle_num):
            total += np.array(Pbest_list[i])
        for j in range(self.particle_dim):
            mbest.append(list(total)[j] / self.particle_num)
        
        #### 2.3.2 位置更新
        ##### Pbest_list更新
        for i in range(self.particle_num):
            a = random.uniform(0,1)
            Pbest_list[i] = list(np.array([x * a for x in Pbest_list[i]]) + np.array([y * (1 - a) for y in gbest_parameter]))
        ##### particle_loc更新
        for j in range(self.particle_num):
            mbest_x = []  ## 存储mbest与粒子位置差的绝对值
            for m in range(self.particle_dim):
                mbest_x.append(abs(mbest[m] - particle_loc[j][m]))
            u = random.uniform(0,1)
            if random.random() > 0.5:
                particle_loc[j] = list(np.array(Pbest_list[j]) + np.array([self.alpha * math.log(1 / u) * x for x in mbest_x]))
            else:
                particle_loc[j] = list(np.array(Pbest_list[j]) - np.array([self.alpha * math.log(1 / u) * x for x in mbest_x]))
                
        #### 2.3.3 将更新后的量子位置参数固定在[min_value,max_value]内 
        ### 每个参数的取值列表
        parameter_list = []
        for i in range(self.particle_dim):
            tmp1 = []
            for j in range(self.particle_num):
                tmp1.append(particle_loc[j][i])
            parameter_list.append(tmp1)
        ### 每个参数取值的最大值、最小值、平均值   
        value = []
        for i in range(self.particle_dim):
            tmp2 = []
            tmp2.append(max(parameter_list[i]))
            tmp2.append(min(parameter_list[i]))
            value.append(tmp2)
        
        for i in range(self.particle_num):
            for j in range(self.particle_dim):
                particle_loc[i][j] = (particle_loc[i][j] - value[j][1])/(value[j][0] - value[j][1]) * (self.max_value - self.min_value) + self.min_value
                
        return particle_loc

## 2.4 画出适应度函数值变化图
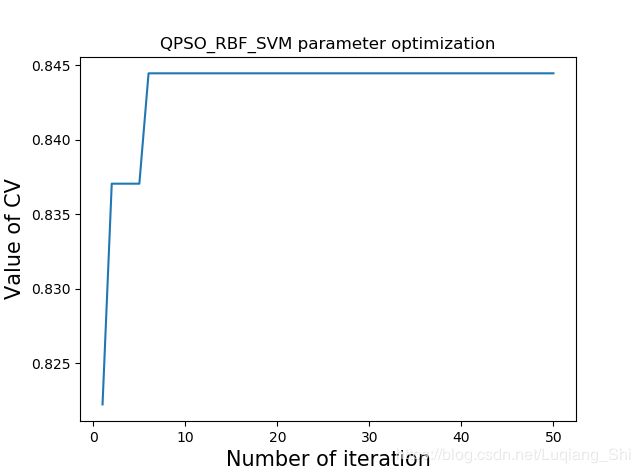
    def plot(self,results):
        '''画图
        '''
        X = []
        Y = []
        for i in range(self.iter_num):
            X.append(i + 1)
            Y.append(results[i])
        plt.plot(X,Y)
        plt.xlabel('Number of iteration',size = 15)
        plt.ylabel('Value of CV',size = 15)
        plt.title('QPSO_RBF_SVM parameter optimization')
        plt.show()         

## 2.5 主函数
    def main(self):
        results = []
        best_fitness = 0.0 
        ## 1、粒子群初始化
        particle_loc = self.swarm_origin()
        ## 2、初始化gbest_parameter、pbest_parameters、fitness_value列表
        ### 2.1 gbest_parameter
        gbest_parameter = []
        for i in range(self.particle_dim):
            gbest_parameter.append(0.0)
        ### 2.2 pbest_parameters
        pbest_parameters = []
        for i in range(self.particle_num):
            tmp1 = []
            for j in range(self.particle_dim):
                tmp1.append(0.0)
            pbest_parameters.append(tmp1)
        ### 2.3 fitness_value
        fitness_value = []
        for i in range(self.particle_num):
            fitness_value.append(0.0)
        
        ## 3、迭代
        for i in range(self.iter_num):
            ### 3.1 计算当前适应度函数值列表
            current_fitness_value,current_best_fitness,current_best_parameter = self.fitness(particle_loc)
            ### 3.2 求当前的gbest_parameter、pbest_parameters和best_fitness
            for j in range(self.particle_num):
                if current_fitness_value[j] > fitness_value[j]:
                    pbest_parameters[j] = particle_loc[j]
            if current_best_fitness > best_fitness:
                best_fitness = current_best_fitness
                gbest_parameter = current_best_parameter
            
            print('iteration is :',i+1,';Best parameters:',gbest_parameter,';Best fitness',best_fitness)
            results.append(best_fitness)
            ### 3.3 更新fitness_value
            fitness_value = current_fitness_value
            ### 3.4 更新粒子群
            particle_loc = self.updata(particle_loc,gbest_parameter,pbest_parameters)
        ## 4.结果展示
        results.sort()
        self.plot(results)
        print('Final parameters are :',gbest_parameter)

最优适应度函数值随迭代次数的变化如下图：

参考资料

1、https://blog.csdn.net/Luqiang_Shi/article/details/84720738
2、郑伟博. 粒子群优化算法的改进及其应用研究[D]. 2016.