R语言案例分析：财政收入的多元相关与回归分析

R语言案例分析：财政收入的多元相关与回归分析

数据集下载 （mvcase3.xls）中的表Case3。

 y：财政收入
 x1：国内生产总值
 x2：能源消费总量
 x3：从业人员总数
 x4：全社会固定资产投资总额
 x5：实际利用外资总额
 x6：全国城乡居民储蓄存款年底余额
 x7：居民人均消费水平
 x8：消费品零售总额
 x9：居民消费价格指数

case3 <- read.table("clipboard", header = T, sep = "\t")
head(case3)

        y      x1        x2        x3         x4       x5       x6       x7    x8      x9
1 1146 4038 58588 41024  849.4 31.14  281.0 197 1800 102.0
2 1160 4518 60257 42361  910.9 31.14  399.5 236 2140 108.1
3 1176 4860 59447 43725  961.0 31.14  523.7 249 2350 110.7
4 1212 5302 62067 45295 1230.4 31.14  675.4 266 2570 112.8
5 1367 5957 66040 46436 1430.1 19.81  892.5 289 2849 114.5
6 1643 7207 70904 48197 1832.9 27.05 1214.7 327 3376 117.7

summary(case3)

            y                      x1                            x2                     x3                           x4                             x5         
 Min.   : 1146       Min.   : 4038        Min.   :  7668         Min.   :41024       Min.   :  849        Min.   : 19.8  
 1st Qu.: 1643     1st Qu.: 7207      1st Qu.: 66040     1st Qu.:48197     1st Qu.: 1833     1st Qu.: 31.1  
 Median : 2665   Median :16918   Median : 96934   Median :55329   Median : 4517   Median :102.3  
 Mean   : 3896     Mean   :28471    Mean   : 93109    Mean   :57401     Mean   : 9536    Mean   :218.8  
 3rd Qu.: 5218    3rd Qu.:46670    3rd Qu.:122000    3rd Qu.:67199     3rd Qu.:17042   3rd Qu.:432.1  
 Max.   :11444     Max.   :80423      Max.   :138948     Max.   :70586      Max.   :29855     Max.   :644.1  
       x6                       x7                      x8                        x9     
 Min.   :  281         Min.   : 197      Min.   : 1800        Min.   :102  
 1st Qu.: 1215     1st Qu.: 327     1st Qu.: 3376     1st Qu.:118  
 Median : 5196   Median : 762   Median : 8101   Median :203  
 Mean   :14871   Mean   :1149   Mean   :11244   Mean   :215  
 3rd Qu.:21519   3rd Qu.:1746   3rd Qu.:16265   3rd Qu.:310  
 Max.   :59622     Max.   :3143     Max.   :31135    Max.   :381

cor(case3) #相关分析

        y             x1          x2          x3          x4        x5        x6          x7        x8         x9
y  1.0000 0.9852 0.7718 0.8337 0.9867 0.9383 0.9954 0.9866 0.9910 0.9341
x1 0.9852 1.0000 0.8254 0.8646 0.9969 0.9783 0.9848 0.9995 0.9972 0.9752
x2 0.7718 0.8254 1.0000 0.8734 0.8077 0.8392 0.7608 0.8231 0.8232 0.8863
x3 0.8337 0.8646 0.8734 1.0000 0.8453 0.8556 0.7999 0.8641 0.8688 0.9264
x4 0.9867 0.9969 0.8077 0.8453 1.0000 0.9776 0.9858 0.9953 0.9925 0.9622
x5 0.9383 0.9783 0.8392 0.8556 0.9776 1.0000 0.9398 0.9738 0.9641 0.9721
x6 0.9954 0.9848 0.7608 0.7999 0.9858 0.9398 1.0000 0.9857 0.9879 0.9260
x7 0.9866 0.9995 0.8231 0.8641 0.9953 0.9738 0.9857 1.0000 0.9986 0.9745
x8 0.9910 0.9972 0.8232 0.8688 0.9925 0.9641 0.9879 0.9986 1.0000 0.9697
x9 0.9341 0.9752 0.8863 0.9264 0.9622 0.9721 0.9260 0.9745 0.9697 1.0000

plot(case3) #矩阵散点图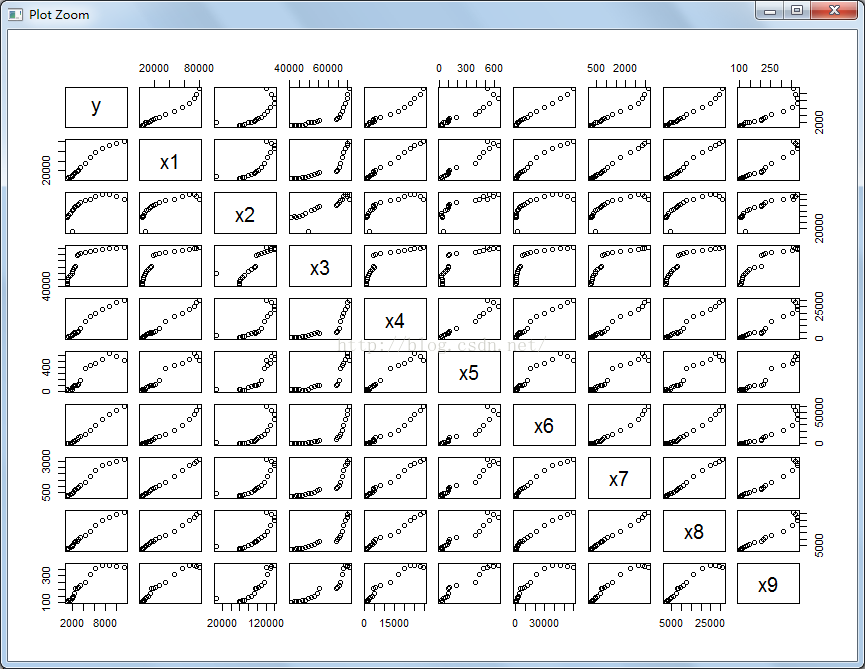

library(psych)
corr.test(case3) #psych包中的corr.test()函数可进行统计显著性检验

Call:corr.test(x = case3)
Correlation matrix 
       y       x1      x2   x3     x4     x5     x6    x7    x8    x9
y  1.00  0.99 0.77 0.83 0.99 0.94 1.00 0.99 0.99 0.93
x1 0.99 1.00 0.83 0.86 1.00 0.98 0.98 1.00 1.00 0.98
x2 0.77 0.83 1.00 0.87 0.81 0.84 0.76 0.82 0.82 0.89
x3 0.83 0.86 0.87 1.00 0.85 0.86 0.80 0.86 0.87 0.93
x4 0.99 1.00 0.81 0.85 1.00 0.98 0.99 1.00 0.99 0.96
x5 0.94 0.98 0.84 0.86 0.98 1.00 0.94 0.97 0.96 0.97
x6 1.00 0.98 0.76 0.80 0.99 0.94 1.00 0.99 0.99 0.93
x7 0.99 1.00 0.82 0.86 1.00 0.97 0.99 1.00 1.00 0.97
x8 0.99 1.00 0.82 0.87 0.99 0.96 0.99 1.00 1.00 0.97
x9 0.93 0.98 0.89 0.93 0.96 0.97 0.93 0.97 0.97 1.00
Sample Size 
[1] 21
Probability values (Entries above the diagonal are adjusted for multiple tests.) 
   y x1 x2 x3 x4 x5 x6 x7 x8 x9
y  0  0  0  0  0  0  0  0  0  0
x1 0  0  0  0  0  0  0  0  0  0
x2 0  0  0  0  0  0  0  0  0  0
x3 0  0  0  0  0  0  0  0  0  0
x4 0  0  0  0  0  0  0  0  0  0
x5 0  0  0  0  0  0  0  0  0  0
x6 0  0  0  0  0  0  0  0  0  0
x7 0  0  0  0  0  0  0  0  0  0
x8 0  0  0  0  0  0  0  0  0  0
x9 0  0  0  0  0  0  0  0  0  0

 To see confidence intervals of the correlations, print with the short=FALSE option

从相关分析结果可以看出，y与x1，x2，x3，x4，x5，x6，x7，x8，x9 的关系都非常密切。其中，y与x6之间的关系最为密切（r=0.9954，p=0<0.001）。

fm <- lm(y~., data=case3) #线性回归

summary(fm)

Call:
lm(formula = y ~ ., data = case3)


Residuals:
   Min     1Q     Median     3Q    Max 
-282.0  -63.3   26.9     90.6      200.8 


Coefficients:
                     Estimate    Std. Error     t value    Pr(>|t|)  
(Intercept)  -1.43e+02   6.28e+02   -0.23    0.824  
      x1          -1.14e-01   1.03e-01   -1.10    0.293  
      x2          -4.42e-03   2.85e-03   -1.55    0.149  
      x3           3.04e-02   1.58e-02    1.92    0.082 .
      x4           2.29e-01   7.38e-02    3.11    0.010 *
      x5          -7.92e-01   1.46e+00   -0.54    0.598  
      x6           1.16e-01   4.35e-02    2.68    0.022 *
      x7          -1.49e+00   2.71e+00   -0.55    0.592  
      x8           3.01e-01   1.59e-01    1.89    0.085 .
      x9           2.52e+00   6.84e+00    0.37    0.719  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 161 on 11 degrees of freedom
Multiple R-squared:  0.999, Adjusted R-squared:  0.997 
F-statistic:  815 on 9 and 11 DF,  p-value: 3.14e-14

得到的线性回归模型如下：

y = -143 - 0.114x1 - 0.0044x2 + 0.0304x3 + 0.229x4 - 0.792x5 + 0.116x6 - 1.49x7 + 0.301x8 + 2.52x9

从回归分析可知，对y（财政收入）影响显著的有 x4（全社会固定资产投资总额）和x6（全国城乡居民储蓄存款年底余额）

下面利用该回归模型计算出的财政收入总量与实际财政收入总量作出折线图：

y <- case3$y
yhat <- fm$fitted.values #拟合模型的预测值

t <- 1978:1998
plot(t, y)
lines(t, yhat)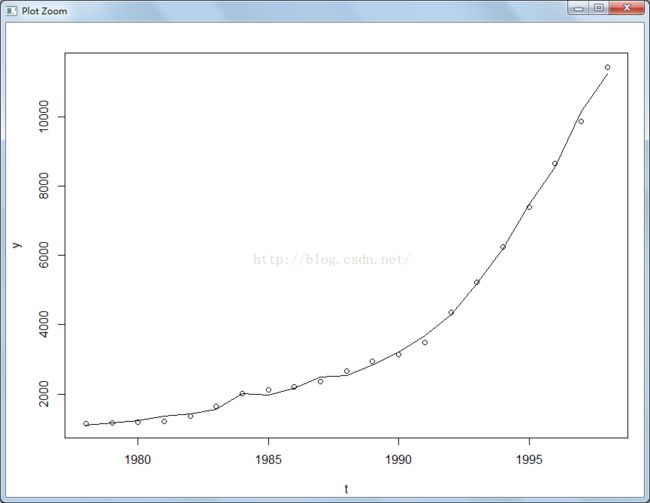

拟合性相当好，点和线几乎重合。

                                                                                                                                                                                                                                      来自《多元统计分析及R语言建模》 第四版