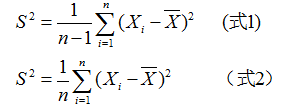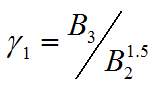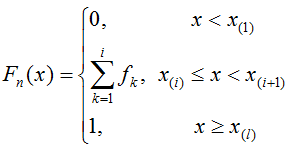4 描述性统计量和统计图

更多MATLAB数据分析视频请点击，或者在网易云课堂上搜索《MATLAB数据分析与统计》 http://study.163.com/course/courseMain.htm?courseId=1003615016

.描述性统计量包括均值、方差、标准差、最大值、最小值、极差、中位数、分位数、众数、变异系数、中心矩、原点炬、偏度、峰度、协方差和相关系数。

 统计图包括箱线图、直方图、经验分布函数图、正态概率图、P-P图和Q-Q图。

本章以下表中的数据示例，对其进行操作演示。

1 .描述性统计量包括均值、方差、标准差、最大值、最小值、极差、中位数、分位数、众数、变异系数、中心矩、原点炬、偏度、峰度、协方差和相关系数。

  1.1 均值

    MATLAB中用mean函数来计算样本均值，样本均值描述了样本观测数据取值相对集中的中心位置。

    例：用mean函数计算工作表中的平均成绩（计算平均成绩的时候要去掉缺考的成绩，即成绩为0的）

  %读取文件1.xls中的第一个工作表中的总成绩的数据即G2：G52,默认的就是读取第一个工作表中的数据，无需指定
%score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','Sheet1','G2:G52');
  score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','G2:G52');
  score=score(score>0);  %只把成绩不为0的数据取出来，即去掉缺考成绩
  score_mean=mean(score)     %调用mean函数计算平均值

  score_mean =

      79
 有时候样本均值会掩盖很多信息，你和马云平均一下你也是亿万土豪，这说明了样本均值受异常值的影响比较大，有一定的不合理性。

 1.2 方差和标准差

  样本方差有如下两种形式的定义：

 

 

   样本标准差是样本方差的算术平方根，相应的它也有两种形式的定义：

 

  样本方差或标准差表述了样本观测数据变异程度的大小，MATLAB统计工具箱中提供了var和std函数，分别用来计算样本方差和标准差。

 调用格式

  var（x）=var（x，0）：用公式1计算方差

  var（x，1）                  ：用公式2计算方差

 std（x）=std（x，0）：用公式3计算标准差

 std（x，1）                   ：用公式4计算标准差

例：对上一列中的数据中的总成绩求方差和标准差

%读取文件1.xls中的第一个工作表中的总成绩的数据即G2：G52,默认的就是读取第一个工作表中的数据，无需指定
%score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','Sheet1','G2:G52');
score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','G2:G52');
score=score(score>0);  %只把成绩不为0的数据取出来，即去掉缺考成绩

%计算方差和标准差
ss1=var(score)  %式1
ss1=var(score)  %式1
ss2=var(score,1) %式2
s1=std(score)    %式3
s1=std(score,0)   %式3
s2=std(score,1)   %式4

ss1 =

   103


ss1 =

   103


ss2 =

  100.8980


s1 =

   10.1489


s1 =

   10.1489


s2 =

   10.0448

 1.3 最大值和最小值

 max函数用来计算样本最大值，min函数用来计算样本最小值

score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','G2:G52');
score=score(score>0);  %只把成绩不为0的数据取出来，即去掉缺考成绩

score_max=max(score)
score_min=min(score)

score_max =

    98


score_min =

    49

 1.4 极差

  range函数用来计算样本的极差（最大值-最小值），极差可以作为样本观测数据变异程度大小的一个简单度量

  score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','G2:G52');
  score=score(score>0);  %只把成绩不为0的数据取出来，即去掉缺考成绩

  score_range=range(score)

score_range =

    49

1.5 中位数

 将样本观测值从小到大依次排列，位于中间的那个观测值，称为样本中位数，它描述了样本观测数据的中间位置。median函数用来计算样本的中位数

 score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','G2:G52');
score=score(score>0);  %只把成绩不为0的数据取出来，即去掉缺考成绩
 score_meidan=median(score)

score_meidan =

    80

1.6 分位数

分位数就是先把一列数按从小到大排序,如果一共有n个数,那么四分之一分位数就是第n*0.25个数,四分之三分位数就是第n*0.75个数,以此类推,p分位数就是第n*p个数.如果n*p不是整数则往最接近的较大的整数上归。样本的0.5分位数就是样本的中位数。

MATLAB统计工具箱中提供了quantile和prctilte，均可用来计算样本的分位数，一个用小数表示分位数，一个用百分数表示分位数

score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','G2:G52');
score=score(score>0);  %只把成绩不为0的数据取出来，即去掉缺考成绩

score_m1=quantile(score,[0.25,0.5,0.75])  %计算样本的0.25，0.5,0.75分位数
 socre_m2=prctile(score,[25,50,75])  %计算样本的25%，50%，75%分位数

score_m1 =

   73.0000   80.0000   85.5000


socre_m2 =

   73.0000   80.0000   85.5000

1.7 众数

  众数描述了样本数据中出现次数最多的数。mode函数用来计算样本的众数

 score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','G2:G52');
score=score(score>0);  %只把成绩不为0的数据取出来，即去掉缺考成绩

score_mode=mode(score)

score_mode =

    80

1.8 变异系数

 变异系数是衡量数据变异程度的（和方差标准差一样），当进行两个或多个变量变异程度的比较时，如果平均值相同，可以直接用标准差来比较。如果平均值不同，比较其变异程度就不能用标准差，而需要采用标准差与平均数的比值来比较。标准差与平均值的比值称为变异系数。MATLAB中没有专门计算变异系数的函数，需要利用std和mean函数的比值来计算

  score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','G2:G52');
  score=score(score>0);  %只把成绩不为0的数据取出来，即去掉缺考成绩

  score_cvar=std(score)/mean(score)  %计算变异系数

 score_cvar =

    0.1285

1.9  原点矩

 定义样本的k阶元电矩为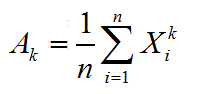，（样本数据的k次长的均值），样本的1阶原点矩就是样本均值

  score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','G2:G52');
  score=score(score>0);  %只把成绩不为0的数据取出来，即去掉缺考成绩

 A2=mean(score.^2)

A2 =

   6.3419e+03

1.10 中心矩

  定义样本的k阶中心矩为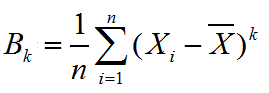，（样本中个元素减去均值的k次方的均值），显然，样本的1阶中心矩为0，二阶中心矩为样本的方差。moment函数用来计算样本的k阶中心矩

  score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','G2:G52');
  score=score(score>0);  %只把成绩不为0的数据取出来，即去掉缺考成绩

  B1=moment(score,1)  %计算样本的1阶中心矩
 B2=moment(score,2)  %计算样本的2阶中心矩

B1 =

     0


B2 =

  100.8980

1.11 偏度

 样本偏度反映了总体分布的对称信息，偏度越接近0，说明分布越对称，否则分布越偏斜。若偏度为负，说明样本服从左偏分布（概率密度的左尾巴长，顶点偏向右边）；若偏度为正，样本服从有偏分布（概率密度的右尾巴长，顶点偏向左边），MATLAB中的skewness函数用来计算样本的偏度，计算公式为

 

其中B2和B3分别为样本的2阶和3阶中心矩。

  score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','G2:G52');
  score=score(score>0);  %只把成绩不为0的数据取出来，即去掉缺考成绩

 score_skewness=skewness(score)  %计算样本偏度

score_skewness =

   -0.7929

1.12 峰度

  样本峰度反映了总体分布密度曲线在其峰值附近的陡峭程度。正态分布的峰度为3，如果样本峰度大于3，说明总体分布密度曲线在其峰值附近比正态分布来得陡。反之，小于 3，说明总体分布密度曲线在其峰值附近比正态分布平缓。计算公式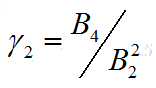，B2，B4分别是样本的2阶和4阶中心矩，MATLAB中kurtosis函数用来计算样本峰度。

  score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','G2:G52');
  score=score(score>0);  %只把成绩不为0的数据取出来，即去掉缺考成绩

  score_kurtosis=kurtosis(score)

 score_kurtosis =

    4.3324

1.13 协方差

  协方差是描述变量间相关程度的统计量。两随机向量X,Y之间的协方差定义为cov(X,Y)=E[(X-E(X))(Y-E(Y))],，E表示数学期望，MATLAB中用cov函数用来计算变量间的协方差矩阵。

all函数：检测矩阵中是否全为非零元素
any函数：检测矩阵中是否有非零元素，如果有，则返回1，否则，返回0。用法和all一样

用法：

B=all(A)

B=all(A.dim); %dim=1或dim=2

B = all(A)：
如果A是一个向量，如果所有的元素都是非零的，则返回1，如果有一个元素为零，则返回0。
如果A是一个矩阵，则返回一个行向量，用于检测每一列是否全为非零元素，如果某一列中有一个元素为零，则返回0，如果某一列中全为非零元素，则返回1，由此构成一个行向量。
B = all(A, 1)
返回一个行向量，可以认为all(A, 1)等价于all(A)

B = all(A, 2)
返回一个列向量，用于检测每一行是否全为非零元素，如果某一行中有一个元素为零，则返回0，如果某一行中全为非零元素，则返回1，由此构成一个列向量。

%计算平时成绩和期末成绩间的协方差（平时成绩与期末成绩的相关程度）
 %需要读取平时成绩和期末成绩这两列
 XY=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','E2:F52');
 XY=XY(all(XY,2),:);
 conXY=cov(XY)

conXY =

    9.2245   19.8588
   19.8588   54.0578

返回的conXY是一个2x2的对称矩阵，即平时成绩与期末成绩的协方差矩阵。其中，主对角线上的9.2245是平时成绩的方差，54.0578是期末成绩的方差。副对角线上的19.8588是平时成绩与期末成绩的协方差

1.14 相关系数

 在用协方差描述变量间的相关程度时会受到变量的量纲和数量级的影响，即使对于同样的一组变量，当变量的量纲和数量级发生变化时，协方差也会随之改变。因此，应先对变量先标准化变换，然后再计算协方差，把先标准化变换后做协方差运算定义为变量间的相关系数，相关系数是一个无单位的量，绝对值不超过1，它描述了变量间的线性相关程度。当变量间相关系数为0时，变量间不存在线性趋势关系，但可能存在非线性趋势关系；当变量间相关系数的绝对值为1时，一个变量是另一变量的线性函数；当变量间相关系数越接近1时，变量间线性趋势越明显。MATLAB中的corrcoef函数用来计算变量间相关系数矩阵。

 XY=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','E2:F52');
 XY=XY(all(XY,2),:);

Rxy=corrcoef(XY)  %计算平时成绩与期末成绩的相关系数

Rxy =

    1.0000    0.8893
    0.8893    1.0000

由结果可以看出，平时成绩与期末成绩的相关系数为0.8893，说明平时成绩与期末成绩间存在明显的线性递增趋势。

2. 统计图

 2.1 箱线图

箱线图，又称作箱须图（box-whiskerplot）是利用数据中的五个特征值——最小值、第一四分位点、中值、第三四分位点、最大值来描述数据的图形。箱线图可以粗略的估计数据是否具有对称性，粗略观察数据的分散程度，特别可用于对几个样本的比较。

 

箱线图的做法：

 （1）画一个箱子，其左侧线为样本0.25分位数m0.25位置，右侧线为样本0.75分位数m0.75位置，在样本中位数（即0.5分位数m0.5）位置上画一条数线，画在箱子内。这个箱子包含了样本中50%的数据

 （2）在箱子左右两侧各引出一条水平线，左侧画直max{min（x），m0.25-1.5（m0.75-m0.25）}，右侧画值min（max（x），m0.25+1.5（m0.75-m0.25）），落在左右边界之外的样本点被称为异常点，用红色‘+’号标出。

 箱线图非常直观地反映了样本数据的分散程度以及总体分布的对称性，利用箱线图可以直观的识别样本中的异常值。

MATLAB统计工具箱中提供了boxplot函数绘制箱线图。

调用格式：

boxplot（X，‘Name’，value）；

‘Name’是箱线图的一些属性，value是该属性的值

例如：

Name为‘notch’，当value为on时，产生的是凹盒图（有切口的box图），off时产生矩箱图（无切口的box图）。

Name为‘orientatiaon’，当value为horizontal时，箱图是水平画的，vertical时为垂直箱图

 score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','G2:G52');
  score=score(score>0);  %只把成绩不为0的数据取出来，即去掉缺考成绩

  figure;
 boxlabel={'考试成绩箱线图'};  %箱线图的标签
 boxplot(score,boxlabel,'notch','on','orientation','horizontal');
% boxplot(score)
 xlabel('考试成绩');

2.2 频数（频率）直方图

 频数（频率）直方图的做法如下：

 (1)将样本观测值x1，x2，......,xn从小到大排序并去除多余的重复值，得到x(1)

 (2)适当选取略小于与x(1)的数a和略大于x(l)的数b，将区间(a,b)随意分为k个不想交的小区间，记第i个小区间为Ii，其长度为hi。

 (3)把样本观测值逐个分到各区间内，并计算样本观测值落在各区间内的频数ni，及频率fi=ni/n.

 (4)在x轴上截取各区间，并以各区间为底，以ni为高左小矩形，就得到频数直方图；如果以fi=ni/n为高做小矩形，就得到频率直方图。

  MATLAB统计工具箱中提供了hist函数用来绘制频数直方图，用法

 hist(x,n):  x是要统计的数据，n表示用多少个小矩形（默认10个）

  还提供了ecdf和ecdfhist函数，用来绘制频率直方图

   [f,xc]=ecdf(x) :  调用ecdf函数计算xc处的经验分布函数值f，返回值作为ecdfhist函数的参数绘制频率直方图

   ecdfhist(f,xc,n) :n表示用多少个小矩阵（默认10个）

例：

 score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','G2:G52');
  score=score(score>0);  %只把成绩不为0的数据取出来，即去掉缺考成绩

figure;
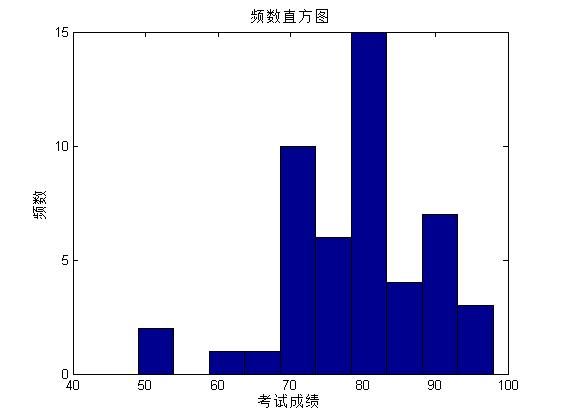
 hist(score);
 xlabel('考试成绩')
 ylabel('频数')
 title('频数直方图');
 
 figure;
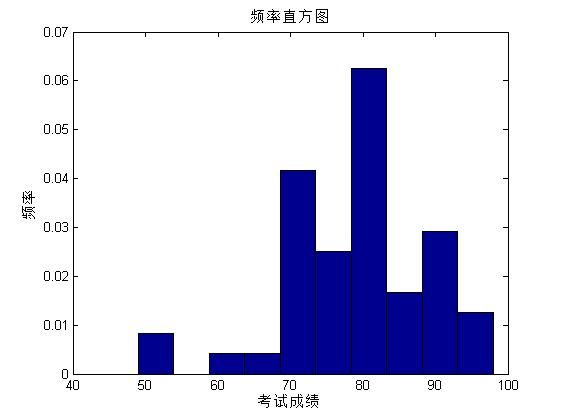
 [f,xc]=ecdf(score);
 ecdfhist(f,xc);
 xlabel('考试成绩')
 ylabel('频率');
 title('频率直方图');

 

2.3 经验分布函数图

根据2.2中直方图的做法，可以得到样本频数和频率分布表如下所示

观测值          x(1)      x(2)  ........     x(l)          总计

频数               n1        n2   ........       nl             n

频率               f1          f2   .........       fl              1

样本分布函数（经验分布函数）到定义为

经验分布函数图是阶梯状态，反映了样本观测数据分布情况。

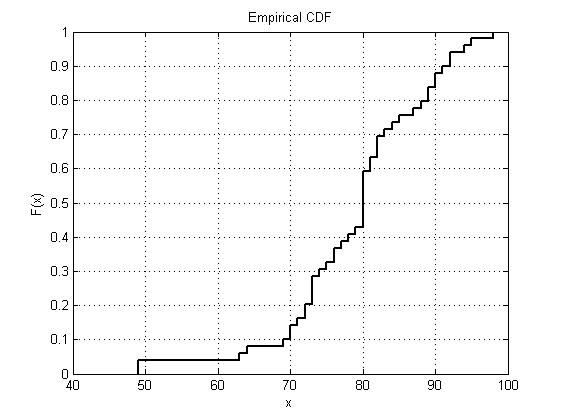
MATLAB统计工具箱中提供了cdfplot函数来绘制样本经验分布函数图，ecdf函数计算各点处的经验分布函数值

用法：

[h,stats]=cdfplot(x):   x是输入的数据，返回值h为图形句柄，stats为结构变量，stats中有5个字段，分别对应最小值、最大值、平均值、中位数和标准差

[f,xc]=ecdf(x) :  x是输入数据，返回xc处的经验分布函数值f，xc向量的长度为length(x)+1

例：

score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','G2:G52'); score=score(score>0);  %只把成绩不为0的数据取出来，即去掉缺考成绩

figure;
[h,stats]=cdfplot(score)
set(h,'color','k','linewidth',2); %设置一下图形h的属性，便于观察
% [f,xc]=ecdf(score)
% figure;
% plot(xc,f)

2.4 正态概率图

正态概率图用于正态分布的检验，正态分布的概率图描绘的是一条直线（参考线），每一个样本观测值对应上的一个‘+’号，如果图中的‘+’号都集中在参考线附加，说明样本观测数据近似服从正态分布；若果偏离参考线的‘+’号越多，说明样本观测数据不服从正态分布。

MATLAB统计工具箱中提供了normplot函数，用来绘制正态概率图。

调用格式：

normplot（x）：x是输入的数据

score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','G2:G52');
score=score(score>0);  %只把成绩不为0的数据取出来，即去掉缺考成绩

figure;
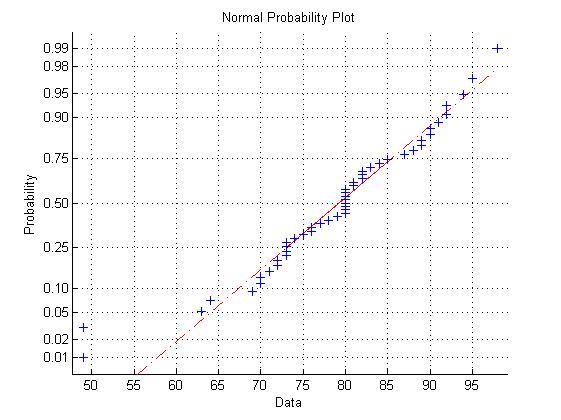
normplot(score)

从图中可以发现，处理左下角两个异常点之外，其余的‘+’号均在参考线附加，说明输入的数据近似服从正态分布。

2.5 p-p图

 p-p图用来检测数据是否服从指定的分布，和normplot定义类似，normplot函数是检测是否服从正态分布，而porbplot不仅可以检测是否服从正态分布，还可以检测是否服从其他指定的分布，只需在调用函数的时候指定一下是哪种分布。

 调用格式：

 probplot('name',x) :x是输入检验的数据，‘name’指定检验哪种分布，name可以取

name                说明

exponential      指数分布

extreme value  极值分布

lognormal           对数分布

normal                正态分布

rayleigh                瑞利分布

weibull                 韦伯分布

例：

score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','G2:G52');
score=score(score>0);  %只把成绩不为0的数据取出来，即去掉缺考成绩

figure;
probplot('normal',score)

和用normplot函数检验结果是一样的。

2.6 q-q图

 q-q图不仅能检验样本是否服从指定分布，还能检测两个样本是否服从相同的分布。

 MATLAB统计工具箱中提供了qqplot函数绘制q-q图。

 下面调用qqplot函数绘制两个班级成绩数据的q-q图，观测这两个班级的成绩数据是否服从相同的分布。

%读取Excel中的班级数据即B2：B52
banji=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','B2:B52');

%读取总成绩数据，即G2:G52中的数据
score=xlsread('C:\Users\Administrator\Desktop\MATLAB\MATLAB数据分析与统计\chapter4\1.xls','G2:G52');

%去除缺考的数据
banji=banji(score>0);
score=score(score>0);

%提取两个班级的总成绩
score1=score(banji==60101);
score2=score(banji==60102);

%绘制两个班级成绩数据的q-q图
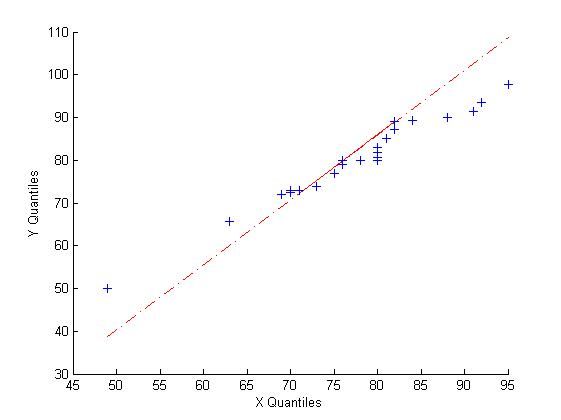
qqplot(score1,score2);

图中可以看，偏离参考线的‘+’号比较多，可以认为两个班的成绩不服从相同的分布

更多MATLAB数据分析视频请点击，或者在网易云课堂上搜索《MATLAB数据分析与统计》 http://study.163.com/course/courseMain.htm?courseId=1003615016