机器学习之二：感知机

1、感知机的原理
感知机的模型为：

f(x)=sign(w⋅x+b)

其中：w和b称为感知机模型的参数， w⊂Rn 叫做权值， b⊂R 叫做偏置，sign为符号函数：

sign(x)={+1,−1,x≥0x<0

感知机的损失函数选择的是误分类点到超平面S的总距离，损失函数定义为：

L(w,b)=−∑xi⊂Myi(w⋅xi+b)

显然，误分类点是负的，如果没有误分类点，损失函数的值为0。误分类点越少，误分类点离超平面越近，损失函数值越小。

2、感知机的学习算法
给定一个训练集:

T={(x1,y1),(x2,y2),...(xn,yn)}

其中 xi⊂Rn,yi⊂{−1,1},i=1,2,..,n， 求参数w,b十七为以下损失函数极小化问题的解

minL(w,b)=−∑xi⊂Myi(w⋅xi+b)

其中M为误分类点的集合。
感知机学习算法是误分类点驱动的，具体采用随机梯度下降算法，首先任取一个超平面 w0,b0 ，然后用随机梯度下降算法不断的极小化目标函数。极小化目标函数不是一次使M中所有的误分类点的梯度下降，而是随机选取一个误分类点时期梯度下降。损失函数 L(w,b) 的梯度由

∇wL(w,b)=−∑xi⊂Myixi

∇bL(w,b)=−∑xi⊂Myi

给出。随机选取一个误分类点 (xi,yi) 对w,b进行更新。

w←w+ηyixi

b←b+ηyi

其中 η（0<η≤1） 是步长，又称为学习率，通过迭代可以期待损失函数 L(w,b) 不断减小，直到为0。
注：一般的，当训练数据集线性可分时，存在穷多个分离超平面可以将两类数据正确分开，感知机利用误分类最小的策略，求得分离超平面，不过这时的解有无穷多个。

3、代码实现
（1）手动实现感知机的算法

import numpy as np
import matplotlib.pyplot as plt
#定义感知机模型
class Perceptron:
    def __init__(self,x,y,a=1):
        self.x=x
        self.y=y
        self.w=np.zeros((x.shape[1],1))#初始化权重，w1,w2均为 0
        self.b=0   # 偏置
        self.a=1   #学习率
        self.numsamples=self.x.shape[0]   # 样本容量
        self.numfeatures=self.x.shape[1]  # 样本特征维度
    # 计算线性函数值
    def sign(self,w,b,x):
        y=np.dot(x,w)+b
        return int(y)
    # 权重和偏置更新
    def update(self,label_i,data_i):
        tmp=label_i*self.a*data_i    #  rate * yi * xi
        tmp=tmp.reshape(self.w.shape)
        #更新w和b
        self.w=tmp+self.w             # w = w+rate * yi * xi
        self.b=self.b+label_i*self.a  # b = b+rate * yi
    # 开始训练
    def train(self):
        isFind=False
        while not isFind:
            count=0
            for i in range(self.numsamples):
                tmpY=self.sign(self.w,self.b,self.x[i,:])
                #如果是一个误分类实例点
                if tmpY*self.y[i]<=0:
                    print '误分类点为：',self.x[i,:],'此时的w和b为：',self.w,self.b
                    count+=1
                    self.update(self.y[i],self.x[i,:])
            if count==0:
                print '最终训练得到的w和b为：',self.w,self.b
                isFind=True
        return self.w,self.b
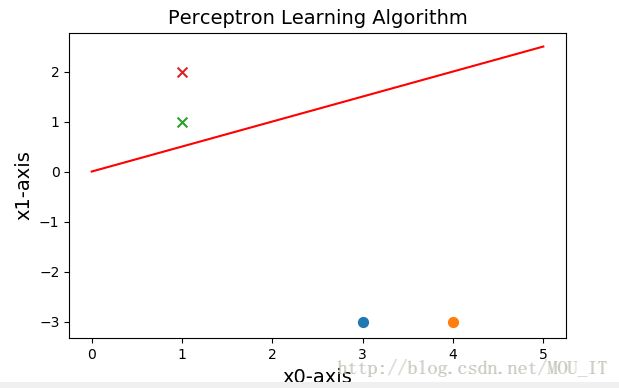
#画图描绘
class Picture:
    def __init__(self,data,w,b):
        self.b=b
        self.w=w
        plt.figure(1)
        plt.title('Perceptron Learning Algorithm',size=14)
        plt.xlabel('x0-axis',size=14)
        plt.ylabel('x1-axis',size=14)
        xData=np.linspace(0,5,100)
        yData=self.expression(xData)
        plt.plot(xData,yData,color='r',label='sample data')
        plt.scatter(data[0][0],data[0][1],s=50)
        plt.scatter(data[1][0],data[1][1],s=50)
        plt.scatter(data[2][0],data[2][1],s=50,marker='x')
        plt.scatter(data[3][0],data[3][1],s=50,marker='x')     
    def expression(self,x):
        y=(-self.b-self.w[0]*x)/self.w[1]#注意在此，把x0，x1当做两个坐标轴，把x1当做自变量，x2为因变量
        return y
    def Show(self):
        plt.show()
if __name__ == '__main__':
  # 创建数据集
  samples=np.array([[3,-3],[4,-3],[1,1],[1,2]])
  labels=[-1,-1,1,1]
  # 初始化感知机，开始训练
  myperceptron=Perceptron(x=samples,y=labels)
  weights,bias=myperception.train()
  # 获得训练结果，并作图
  Picture=Picture(samples,weights,bias)
  Picture.Show()

（2）使用工具包实现感知机算法

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Perceptron

def MyPerceptron(samples,labels):
    #定义感知机
    clf=Perceptron(fit_intercept=True,shuffle=False)
      #1、shuffle:训练数据是否应在每一个时期之后进行调整？
      #2、fit_intercept:截距是否应该估计。如果为false，则数据被假定为已居中。默认为true。    
    #训练感知机
    clf.fit(samples,labels)
    #得到权重矩阵
    weigths=clf.coef_
    #得到截距bisa
    bias=clf.intercept_
    return weigths,bias
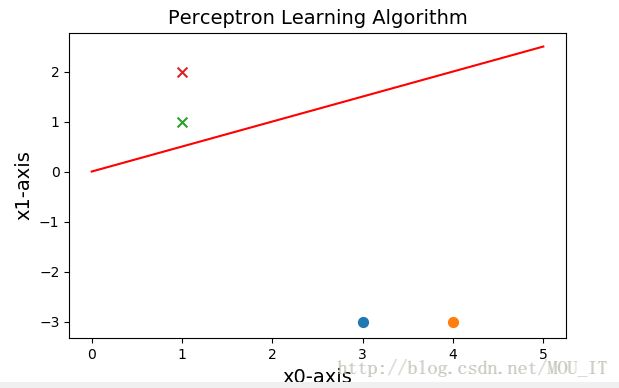
#画图描绘
class Picture:
    def __init__(self,data,w,b):
        self.b=b
        self.w=w
        plt.figure(1)
        plt.title('Perceptron Learning Algorithm',size=14)
        plt.xlabel('x0-axis',size=14)
        plt.ylabel('x1-axis',size=14)
        xData=np.linspace(0,5,100)
        yData=self.expression(xData)
        plt.plot(xData,yData,color='r',label='sample data')
        plt.scatter(data[0][0],data[0][1],s=50)
        plt.scatter(data[1][0],data[1][1],s=50)
        plt.scatter(data[2][0],data[2][1],s=50,marker='x')
        plt.scatter(data[3][0],data[3][1],s=50,marker='x')
        plt.savefig('3d.png',dpi=75)
    def expression(self,x):
        y=(-self.b-self.w[:,0]*x)/self.w[:,1]
        return y
    def Show(self):
        plt.show()
samples=np.array([[3,-3],[4,-3],[1,1],[1,2]])
labels=[-1,-1,1,1]    
weights,bias=MyPerceptron(samples,labels)
print '最终训练得到的w和b为：',weights,',',bias
Picture=Picture(samples,weights,bias)
Picture.Show()