4.pandas数据预处理（完）（数据清洗：重复值、异常值、缺失值；标准化、哑变量、离散化、无监督分箱）

笔记说明：本文是我的学习笔记，大部分内容整理自 黄红梅,张良均等.Python数据分析与应用[M].北京:人民邮电出版社,2018：133-163. 还有部分片断知识来自网络搜索补充。

0.数据来源

来源于这本书，黄红梅,张良均等.Python数据分析与应用[M].北京:人民邮电出版社,2018，的第五章附带数据。
CSDN的数据不可以免费共享，至少要一个金币，有能力的就去下载一下数据下载链接CSDN数据。不方便的，在底下头评论留言，留下邮箱号，我看到之后就会把数据发给你，或者你可以在这本书的出版社网站人民邮电出版社教育社区或者“泰迪杯数据挖掘比赛”泰迪杯数瑞思的网站上找这本书的附带资源，都是免费下载的。

0.1说明

这本书吧，第一部分是pandas和数据库MySQL的对接处理.sql数据。一般的公司的话，有专门的做数据分析的小组或者部门的，需要什么数据跟他们提需求让他们获取，拿.csv就好了。所以我就跳过了sql里面的inner join\outer join\主键合并。我的笔记直接是读取csv数据。
喔还有就是，做这行的话，sql是基础技能，一定要会基础的取数！

1.清洗数据

1.1检测与处理重复值

1.1.1记录重复

import pandas as pd
detail=pd.read_csv("D:\\codes\\python\\data\\detail.csv",  
                   index_col=0,encoding='gbk')

#方法一：定义去重函数
def delrep(list1):
    list2=[]
    for i in list1:
        if i in list1:
            if i not in list2:
                list2.append(i)
    return list2

##去重
dishes=list(detail['dishes_name'])
print('去重前菜品总数是：',len(dishes))
dish=delrep(dishes)
print('方法一去重后数据总数是：',len(dish))

#方法二：利用集合唯一性
print('去重前菜品总数为：',len(dishes))
dish_set=set(dishes)
print(len(dish_set))

这两种方法，区别在，set会将数据顺序打乱。

#方法三：.drop_duplicates
pd.DataFrame(series).drop_duplicates(self,subset=None,keep='first',  
            inplace=False)

参数名字	说明
subset	接收string或sequence，表示进行去重的列，默认none，全部列
keep	接收string，表示重复时保留第几个数据
keep	first：保留第一个；last：最后一个；false：只要有重复就都不保留。默认first
inplace	接收boolean,表示是否在原表上进行操作，默认false

dishes_name=detail['dishes_name'].drop_duplicates()
print(len(dishes_name))

1.1.2特征重复

这里的重复是指，特征之间的相似度=1！所以可以作为特征工程海筛特征的一步！
method参数可以是：spearman,person,kendall
注意这个不能计算分类变量的相似度。

corrdet=detail[['counts','amounts']].corr(method='spearman')
print(corrdet)

corrdet1=detail[['dishes_name','counts','amounts']].corr(method='pearson')
print(corrdet1)

分类变量的话，可以自己写一个判断特征矩阵是否完全相同的函数

1.2检测与处理缺失值

print('缺失值数目是：'，detail.isnull().sum())
print(detail,notnull().sum())

1.2.1删除法

dropna(self, axis=0, how='any', thresh=None,   
subset=None, inplace=False)

参数	说明
asix	0/1,0是对列操作，删除记录行；1是删除列。
how	接收string，表示删除的形式，any表示只要有缺失值就会被删除，all表示当且仅当全部为缺失值时才会执行删除操作，默认any
subset	接收array，表示进行去重的行列。默认是none，表示所有行列
inplace	接收Boolean，表示是否在原表上进行操作，默认是false

print('删除之前',detail,shape)
print('之后',detail.dropna(axis=1).shape)

1.2.2替换法

pd.DataFrame.fillna(self, value=None, method=None, axis=None,  
inplace=False, limit=None, downcast=None, **kwargs)

参数	说明
value	接收scalar，dict，series，dataframe，表示用来替换缺失值，无默认
method	接收待定string。backfill或bfill表示使用下一个非缺失值来填补空缺；pad或ffill表示使用上一个非缺失值来填补，默认none
axis	轴向。1为“跨列！”这个词解释很透彻
inplace	接收Boolean，表示是否在原表上操作，默认False
limit	接收int，表示填补缺失值个数上限，默认none

detail=detail.fillna(777)
print(detail.isnull().sum())

1.2.3插值法

常用的插补法有：线性插补、多项式插补（拉格朗和牛顿）、样条插值
这里使用的是scipy包的interpolate模块

还有这个在图像领域常用的插值法是重心坐标插值，BarycentricInterpolator

from scipy.interpolate import interp1d
import numpy as np
x=np.array([1,2,3,4,5,8,9])
y1=np.array([2,8,18,32,50,128,162]) ##y1=2*x^2
y2=np.array([3,5,7,9,11,17,19])  ##y2=2*x+1

# 线性插补
linearinsvalue1=interp1d(x,y1,kind='linear')
linearinsvalue2=interp1d(x,y2,kind='linear')
print(linearinsvalue1([7,11]),linearinsvalue2([7,11]))

out:[102. 246.] [15. 23.]

# 拉格朗日插补
from scipy.interpolate import lagrange
largeinsvalue1=lagrange(x,y1)
largeinsvalue2=lagrange(x,y2)
print(largeinsvalue1([7,11]),largeinsvalue2([7,11]))
out:[ 98. 242.] [15. 23.]

#样条插补
from scipy.interpolate import spline
splineinsvalue1=spline(x,y1,xnew=np.array([7,11]))
splineinsvalue2=spline(x,y2,xnew=np.array([7,11]))
print(splineinsvalue1,splineinsvalue2)
out:[ 98. 242.] [15. 23.]

对比看到不同方法的准确性哈~
main:1: DeprecationWarning: spline is deprecated!
spline is deprecated in scipy 0.19.0, use Bspline class instead.
这个函数要改变了，以后叫Bspline()

1.3 检测与处理异常值

1.3.1 正态分布的3σ原则

#写一个函数判断数据是否符合均值±3倍标准差的范围
def outrange(data):
    boolind=(data.mean()-3*data.std()>data) | \
    (data.mean()+3*data.std()<data)
    index=np.arange(data.shape[0])[boolind]
    print("这个",index)  ##我就是想近距离感受一下index这个东西
    outrange=data.iloc[index]
    return outrange
outlier=outrange(detail['counts'])
print(outlier.shape[0])
print(outlier.max())

1.3.2箱线图

绘制箱线图之后，这里的异常值标签直接就是fliers，不需要再写函数判断了.

IQR=QL-QU  
QL-1.5*IQR  
QU+1.5*IQR

离群点是通过距离上下四分位数的距离来判断的

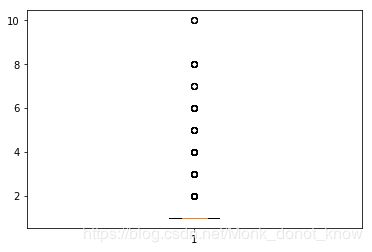
import matplotlib.pyplot as plt
plt.figure(figsize=(6,4))
p=plt.boxplot(detail['counts'].values,notch=True)
outlier1=p['fliers'][0].get_ydata()
plt.show()
print(len(outlier1),max(outlier1),min(outlier1))
print(p)    ###近距离感受一下p的内容
print(p['fliers']) ###p['fliers'][0]获取点的坐标
outlier2=p['fliers'][0].get_xdata() ###再次感受下p['fliers'][0]，就比较明确这个东西了

1.4上栗子！

在1.1.2中省略的自定义函数遍历所有数据分类型数据去重
在& |运算在dataframe上，我走了点弯路，搞了好久才找到一个靠谱的解释。在此排雷，上链接：
这个人的博文第三部分~https://blog.csdn.net/weixin_40041218/article/details/80868521

import pandas as pd
detail = pd.read_csv("D:\\codes\\python\\data\\detail.csv",   
                   index_col=0,encoding='gbk')
print('这个么去重前的样本形状：',detail.shape)
#去重
detail.drop_duplicates(inplace=True)
# 特征去重
def featureEquals(df):
    #这个自定义函数就是说白了就是每一列每一列元素一个一个去做比较，使用的是dataframe.equals函数，返回的是逻辑判断值
    dfequals=pd.DataFrame([],columns=df.columns,index=df.columns)
    for i in df.columns:
        for j in df.columns:
            dfequals.loc[i,j]=df.loc[:,i].equals(df.loc[:,j]) 
    return dfequals
detequals=featureEquals(detail)
print('这个是近距离观察下自定义函数的返回值：',detequals)  

#遍历所有数据
lendet=detequals.shape[0]
dupcol=[]
for k in range(lendet):
    for l in range(k+1,lendet):
        if detequals.iloc[k,l] & \
        (detequals.columns[l] not in dupcol):
            dupcol.append(detequals.columns[l])

#上面的输出结果是dupcol最终是所有的重复列
detail.drop(dupcol,axis=1,inplace=True)
print("去重之后的样本形状：",detail.shape)

2.标准化

2.1离差标准化(min-max标准化)

$$X^{\ast }=\frac{X-min}{max-min}$$

2.1.1上栗子！

import pandas as pd
import numpy as np
detail = pd.read_csv("D:\\codes\\python\\data\\detail.csv",   
                   index_col=0,encoding='gbk')
# 定义函数min-max标准化
def minmaxscale(data):
    data=(data-data.min())/(data.max()-data.min())
    return data 
# 对菜品订单售价和销售做标准化
data1=minmaxscale(detail['counts'])
data2=minmaxscale(detail['amounts'])
data3=pd.concat([data1,data2],axis=1)
print('标准化之前的数据是：\n',detail[['counts','amounts']].head())
print('标准化之后的数据是：\n',data3.head())    

诺，输出结果是这样的：

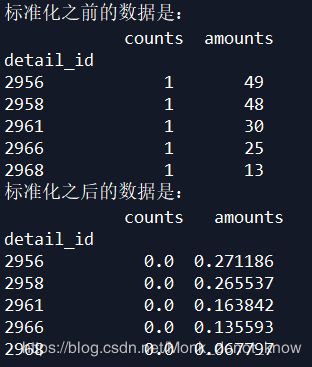
这个标准化有三点需要注意：
a.当数据值=min时，标准 化之后就会等于零；
b.在数据分布不均匀，又极差较大的情况下，标准化之后会出现数据的差别不大的现象；
c.在将来新的数据如果出现比现有数据max还大的情况，就会报错，这时候需要重新设置min,max。

2.2标准差标准化（Z分数标准化）

$$X^{\ast }=\frac{X-\overline{X}}{\delta }$$

2.2.1上栗子！

def standardscale(data):
    data=(data-data.mean())/data.std()
    return data 
# 对菜品订单售价和销售做标准化 
data4=standardscale(detail['counts'])
data5=standardscale(detail['amounts'])
data6=pd.concat([data4,data5],axis=1)
print('标准化之前的数据是：\n',detail[['counts','amounts']].head())
print('标准化之后的数据是：\n',data6.head())   

诺，结果是这样的：

2.3小数定标标准化

这个标准化是第一次见，但是很简单，就是找到数据绝对值最大的那个数，然后除以10^(次方)。将数据映射到[-1,1]这个区间。
$$X^{\ast }=\frac{X}{10^k}$$
这里有点没懂？？？？？？？？？直接除以abs(max)不就行了吗？？？？？？？？看这个栗子的代码，我蒙了，谁给我解释一下啊

2.3.1上栗子！

def decimalscale(data):
    data=data/10**np.ceil(np.log10(data.abs().max()))
    return data
# 对菜品订单售价和销售做标准化 
data7=decimalscale(detail['counts'])
data8=decimalscale(detail['amounts'])
data9=pd.concat([data7,data8],axis=1)
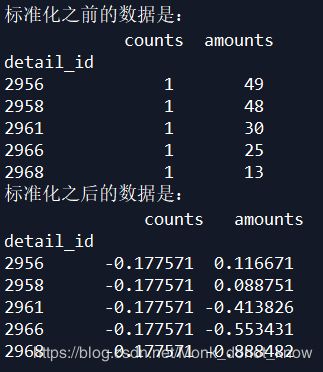
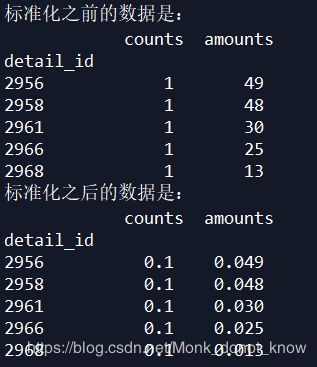
print('标准化之前的数据是：\n',detail[['counts','amounts']].head())
print('标准化之后的数据是：\n',data9.head())    

np.ceil（）就是取，离这个点最近的整数。
这样的话并不能保证端点值是可以取到的啊？？？？疑问
结果是这样的：

3.数据转化

3.1哑变量处理

3.1哑变量处理

get_dummies(data, prefix=None, prefix_sep='_',   
         dummy_na=False, columns=None, sparse=False,   
         drop_first=False, dtype=None)

参数	说明
data	接收array、dataframe或者series。数据
prefix	接收string、string的列表或者dict，表示哑变量处理之后列名的前缀，默认none
prefix_na	接收boolean。表示是否为nan值添加一列。默认false
columns	接收类似list的数据，表示dataframe中需要编码的列名，默认none，表示对所有object和category类型进行编码
sparse	接收Boolean，表示虚拟列是否是稀疏的，默认false
drop_first	接收Boolean，表示是否通过从k个分类别中删除第一级来获得k-1个分类级别，默认false

3.1.1上栗子！

对菜品名称哑变量处理

detail = pd.read_csv("D:\\codes\\python\\data\\detail.csv",encoding='gbk')
data=detail.loc[0:7,'dishes_name']
print('处理前的数据：\n',data.head())
print('处理后：\n',pd.get_dummies(data).head())

诺，结果如下：

3.2离散化连续型数据

首先要明确一下这里的一个概念，这里的方法其实就是特征工程里面常用的一个，无监督分箱法。
这个么，我经常使用卡方分箱方法。我在下一本书的学习也会整理这个知识，不过，网上有现成的，请看下面推荐的两个博客：
可以看这个博客
还有这个

3.2.1等宽法

cut(x, bins, right=True, labels=None, retbins=False,   
precision=3, include_lowest=False, duplicates='raise')

参数	说明
x	接收array或者series，代表需要进行离散化处理的数据，无默认
bins	接收int、list、array、tuple。int的时候，代表离散化后的类别数目；若为序列，则表示进行切分的区间，每两个个数的间隔为一个区间。无默认
right	接收Boolean，代表右侧是否为闭区间，默认true
labels	接收list、array。代表离散化后各个类别的名称。默认空
retbins	接收Boolean，代表是否返回区间标签，默认false
precision	接收int，显示标签的精度，默认3

precision这个参数在np.set_printoptions(precision=4,suppress=True)这里也有，哈哈哈哈哈啊哈，突然想起来，就是调精度的。
numpy精度问题贼烦！不调这个的话，使用numpy随便计算一个矩阵，都有可能算错。比如：看2.1.3这个栗子

price=pd.cut(detail['amounts'],7)
print('离散化7类售价分别的数量是：',price.value_counts())

诺，结果如下：

3.2.2等频法

其实就是利用bins参数的序列进行设置等频区间。

#自定义函数等频法
def sameratecut(data,k):
    w=data.quantile(np.arange(0,1+1.0/k,1.0/k))
    data=pd.cut(data,w)
    print('给我看看这个w是什么','\n',w)
    return data
# 看过w一眼就会明白，dataframe.quantile是设置分位数的函数。
result=sameratecut(detail['amounts'],7).value_counts()
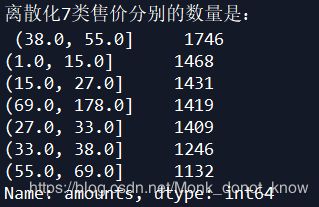
print('离散化7类售价分别的数量是：','\n',result)

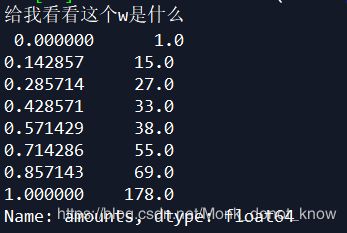
这个dataframe.quantile()就是设置分位数的一个函数。
离散化结果如下：

3.3使用聚类分析等频离散化

def kmeancut(data,k):
    from sklearn.cluster import KMeans
    # 这个模型下一章sklearn介绍
    kmodel=KMeans(n_clusters=k,n_jobs=5)
    kmodel.fit(data.values.reshape((len(detail['amounts']),1)))
    # 输出聚类中心,这个是kmeans函数自带属性，可以直接help(KMeans)查看帮助文档下的Attributes
    c=pd.DataFrame(kmodel.cluster_centers_).sort_values(0)
    #这个就是排了个序，axis=0，列排序
    w=c.rolling(2).mean().iloc[1:] #相邻两项求中点作为边界点
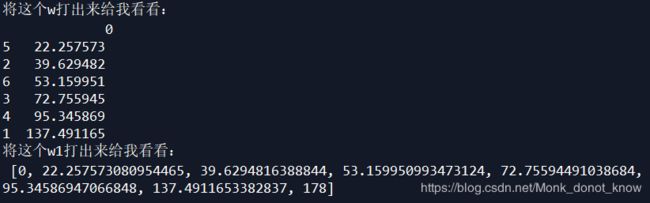
    print('将这个w打出来给我看看：','\n',w)
    w1=[0]+list(w[0])+[data.max()]
    print('将这个w1打出来给我看看：','\n',w1)
    data=pd.cut(data,w1)
    return data
# 菜品售价等频离散化
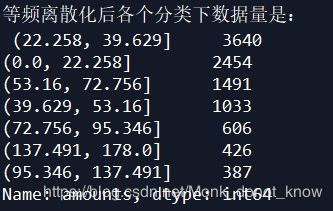
result=kmeancut(detail['amounts'],7).value_counts()
print('等频离散化后各个分类下数据量是：','\n',result)

pd.rolling_mean的使用方法在这里
但是啊，这个方法已经在新的pamdas里面不支持了，这本书有点过时，最新的使用方法是写为：
pd.rolling_mean(D.2) --> D.rolling(2).mean()