单源最短路径
在最短路径问题中,给定一个带权重的有向图G=(V,E)和权重函数w:E→R,该权重函数将每条边映射到实数值的权重上。图中一条路径p=[v0,v1,•••,vk]的权重w(p)是构成该路径的所有边的权重之和。定义从结点u到结点v的最短路径权重δ=(u,v),从结点u到结点v的最短路径则定义为任何一条权重w(p)= δ=(u,v)的从u到v的路径p。
最短路径存在几个变体:
- 单目的地最短路径问题:找到从每个结点v到给定目的地结点t的最短路径。如果将图的每一条边的方向反过来,就可以将整个问题转换为单源最短路径问题。
- 单结点对最短路径问题:找到从给定结点u到给定结点v的最短路径。
- 所有结点对最短路径问题:对于每个结点u和v,找到从结点u到结点v的最短路径。
一些概念和性质
最短路径算法通常依赖最短路径的一个重要性质:两个结点之间的一条最短路径包含着其它的最短路径。在某些单源最短路径问题中可能包括权重为负值的边。如果从结点s到结点v的某条路径上存在权重为负值的环路,则定义δ=(u,v)=-∞。
最短路径的表示
在通常情况下,不但需要计算出最短路径权重,还需要计算出最短路径上的结点。给定图G=(V,E),对于每个结点v,维持一个前驱结点v.π,该前去结点可能是另一个结点或者NIL。最短路径算法将对每个结点的π属性进行设置,这样,将从结点v开始的前驱结点链反转过来,就是从s到v的一条最短路径。给定结点v,且v.π≠NIL,PRINT_PAT(G,s,v)打印出的就是从结点s到结点v 的一条最短路径。
但是,在运行最短路径算法的过程中,π值并不一定能给出最短路径。定义结点集Vπ为图G中的前驱结点不为NIL的结点的集合,再加上源结点s,即Vπ={v∈V:v.π≠NIL}∪{s}。有向边集合Eπ是由Vπ中的结点的π值所诱导的边的集合,即Eπ={(v.π,v) ∈E:v∈Vπ-{s}}。
单源最短路径算法所生成的π值具有如下性质:在算法终止时,Gπ是一棵“最短路径树”。非形式化的说,最短路径树是一棵具有根结点的树,该树包括了从源结点s到每个可以从s到达的结点的一条最短路径。设G=(V,E)是带权重的有向图,其权重函数为w:E→R,假定G不包含从s可以到达的权重为负值的环路。一棵根结点为s的最短路径树是一个有向子图G’=(V’,E’),满足:
- V’是图G中从源结点s可以到达的所有结点的集合。
- G’形成一棵根结点为s的树。
- 对于所有的结点v∈V’,图G’中从结点s到v的唯一简单路径是图G中从结点s到结点v的一条最短路径。
需要指出的是,最短路径不一定是唯一的,最短路径树叶不一定是唯一的。
松弛操作
对于每个结点v来说,为一个属性v.d用来记录从源结点s到结点v的最短路径权重的上界,称v.d为s到v的最短路径估计。使用如下的算法来对最短路径估计和前驱结点进行初始化:
INITIALIZE_SINGLE_SOURCE(G, s)
for each vertex v ∈ G.V
v.d = ∞
v.π = NIL
s.d = 0对一条边(u,v)的松弛过程为:将从结点s到u之间的最短巨鹿加上结点u和v之间的权重,并与当前的s到v的最短路径估计进行比较,如果前者更小,则对v.d和v.π进行更新。
RELAX(u,v,w)
if v.d > u.d + w(u,v)
v.d = u.d + w(u,v)
v.π = u几个性质
最短路径和松弛操作的一些性质如下:
- 三角不等性质:对于任何边(u,v) ∈E,有δ(s,v)≤δ(s,u)+w(u,v)。
- 上界性质:对于所有的结点v∈V,有v.d≥δ(s,v)。一旦v.d的取值达到δ(s,v),其值将不再变化。
- 非路径性质:如果从结点s到结点v之间不存在路径,则总是有v.d=δ(s,v)=∞。
- 收敛性质:对于某些结点u,v∈V,如果s是图G中的一条最短路径,并且在对边(u,v)进行松弛前的任意时间有u.d=δ(s,u),则在之后的所有时间有v.d=δ(s,v)。
- 路径松弛性质:如果p=(v0,v1,•••,vk)是从源结点s=v0到结点vk的一条最短路径,并且我们对p中的边所进行松弛的次序为(v0,v1),(v1,v2),•••,(v(k-1),vk),则vk.d=δ(s,vk)。
- 前驱子图性质:对于所有的结点v∈V,一旦v.d=δ(s,v),则前驱子图是一棵根结点为s的最短路径树。
Bellman-Ford算法
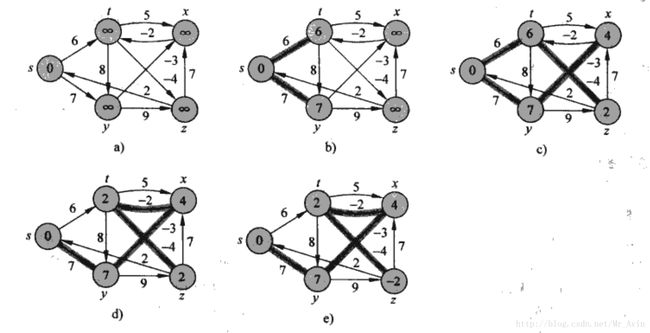
Bellman-Ford算法解决的是一般情况下的单源最短路径问题,边的权重可以为负值。给定带权重的有向图G=(V,E)和权重函数w:E→R,Bellman-Ford算法返回一个布尔值,以表明是否存在一个从源结点可以到达的权重为负值的环路。如果存在这样的一个环路,算法将告诉我们不存在解决方案。如果没有这种环路存在,算法将给出最短路径和它们的权重。
Bellman-Ford算法通过对边进行松弛操作来渐近的降低从源结点s到每个节点v的最短路径的估计值v.d,知道该估计值与实际的最短路径权重δ(s,v)相同时为止。该算法返回TRUE值当且仅当输入图不包含可以从源结点到达的权重为负值的环路。
BELLMAN_FORD(G, w, s)
INITIALIZE_SINGLE_SOURCE(G, s)
for i = 1 to |G.V – 1|
for each edge(u,v) ∈G.E
RELAX(u, v, w)
for each edge(u,v) ∈ G.E
if v.d > u.d + w(u,v)
return FALSE
return TRUEDijkstra算法
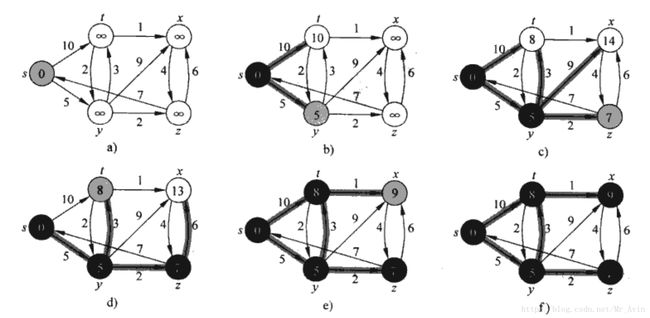
Dijkstra算法解决的是带权重的有向图上单源最短路径问题,该算法要求所有边的权重都为非负值。
Dijkstra算法在运行过程中维持的关键信息是一组结点集合S。从源结点s到该集合中每个结点之间的最短路径已经被找到。算法重复从结点集V-S中选择最短路径估计最小的结点u,将u加入到集合S,然后对所有从u出发的边进行松弛。使用一个最小优先队列Q来保存集合,每个结点的关键值为其d值。
DIJKSTRA(G, w, s)
INITIALIZE_SINGLE_SOURCE(G, s)
S = NULL
Q = G.V
while Q ≠ NULL
u = EXTRACT_MIN(Q)
S = S ∪ {u}
for each vertex v ∈ G.Adj[u]
RELAX(u, v, w)有向无环图的单源最短路径问题
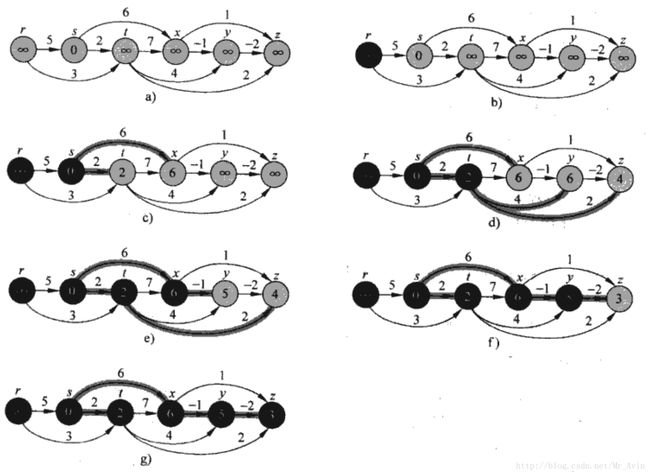
根据结点的拓扑排序次序来对带权重的有向无环图G=(V,E)进行边的松弛操作,便可以计算出从单个源结点到所有结点之间的最短路径。在有向无环图中,即使存在权重为负值的边,但因为没有权重为负值的环路,最短路径都是存在的。
首先对有向无环图进行拓扑排序,确定结点之间的一个线性次序。如果有向无环图包含从结点u到结点v的一条路径,则v在拓扑排序的次序中位于结点v的前面。只需要按照拓扑排序的次序对结点进行一遍处理即可。每次对一个结点进行处理时,对从该结点出发的所有的边进行松弛操作。
DAG_SHORTEST_PATHS(G, w, s)
topologically sort the vertices of G
INITIALIZE_SINGLE_SOURCE(G, s)
for each vertex u, taken in topologically sorted order
for each vertex v ∈ G.Adj[u]
RELAX(u, v, w)