【转】BloomFilter布隆滤波器
转自https://blog.csdn.net/zq602316498/article/details/40660235
在日常生活中,包括在设计计算机软件时,我们经常要判断一个元素是否在一个集合中。
比如在字处理软件中,需要检查一个英语单词是否拼写正确(也就是要判断 它是否在已知的字典中);在 FBI,一个嫌疑人的名字是否已经在嫌疑名单上;在网络爬虫里,一个网址是否被访问过等等。最直接的方法就是将集合中全部的元素存在计算机中,遇到一个新 元素时,将它和集合中的元素直接比较即可。一般来讲,计算机中的集合是用哈希表(hash table)来存储的。它的好处是快速准确,缺点是费存储空间。当集合比较小时,这个问题不显著,但是当集合巨大时,哈希表存储效率低的问题就显现出来 了。比如说,一个象 Yahoo,Hotmail 和 Gmai 那样的公众电子邮件(email)提供商,总是需要过滤来自发送垃圾邮件的人(spamer)的垃圾邮件。一个办法就是记录下那些发垃圾邮件的 email 地址。由于那些发送者不停地在注册新的地址,全世界少说也有几十亿个发垃圾邮件的地址,将他们都存起来则需要大量的网络服务器。如果用哈希表,每存储一亿 个 email 地址, 就需要 1.6GB 的内存(用哈希表实现的具体办法是将每一个 email 地址对应成一个八字节的信息指纹(详见:googlechinablog.com/2006/08/blog-post.html), 然后将这些信息指纹存入哈希表,由于哈希表的存储效率一般只有 50%,因此一个 email 地址需要占用十六个字节。一亿个地址大约要 1.6GB, 即十六亿字节的内存)。因此存贮几十亿个邮件地址可能需要上百 GB 的内存。除非是超级计算机,一般服务器是无法存储的。(该段引用谷歌数学之美:http://www.google.com.hk/ggblog/googlechinablog/2007/07/bloom-filter_7469.html)
一、基本概念
布隆过滤器(Bloom Filter)是由布隆(Burton Howard Bloom)在1970年提出的。它实际上是由一个很长的二进制向量和一系列随机映射函数组成,布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都远远超过一般的算法,缺点是有一定的误识别率(假正例False positives,即Bloom Filter报告某一元素存在于某集合中,但是实际上该元素并不在集合中)和删除困难,但是没有识别错误的情形(即假反例False negatives,如果某个元素确实没有在该集合中,那么Bloom Filter 是不会报告该元素存在于集合中的,所以不会漏报)。
如果想判断一个元素是不是在一个集合里,一般想到的是将所有元素保存起来,然后通过比较确定。链表,树等等数据结构都是这种思路. 但是随着集合中元素的增加,我们需要的存储空间越来越大,检索速度也越来越慢。不过世界上还有一种叫作散列表(又叫哈希表,Hash table)的数据结构。它可以通过一个Hash函数将一个元素映射成一个位阵列(Bit Array)中的一个点。这样一来,我们只要看看这个点是不是 1 就知道可以集合中有没有它了。这就是布隆过滤器的基本思想。
Hash面临的问题就是冲突。假设 Hash 函数是良好的,如果我们的位阵列长度为 m 个点,那么如果我们想将冲突率降低到例如 1%, 这个散列表就只能容纳 m/100 个元素。显然这就不叫空间有效了(Space-efficient)。解决方法也简单,就是使用多个 Hash,如果它们有一个说元素不在集合中,那肯定就不在。如果它们都说在,虽然也有一定可能性它们在说谎,不过直觉上判断这种事情的概率是比较低的。
优点
相比于其它的数据结构,布隆过滤器在空间和时间方面都有巨大的优势。布隆过滤器存储空间和插入/查询时间都是常数。另外, Hash 函数相互之间没有关系,方便由硬件并行实现。布隆过滤器不需要存储元素本身,在某些对保密要求非常严格的场合有优势。
布隆过滤器可以表示全集,其它任何数据结构都不能;
k 和 m 相同,使用同一组 Hash 函数的两个布隆过滤器的交并差运算可以使用位操作进行。
缺点
但是布隆过滤器的缺点和优点一样明显。误算率(False Positive)是其中之一。随着存入的元素数量增加,误算率随之增加。但是如果元素数量太少,则使用散列表足矣。
另外,一般情况下不能从布隆过滤器中删除元素. 我们很容易想到把位列阵变成整数数组,每插入一个元素相应的计数器加1, 这样删除元素时将计数器减掉就可以了。然而要保证安全的删除元素并非如此简单。首先我们必须保证删除的元素的确在布隆过滤器里面. 这一点单凭这个过滤器是无法保证的。另外计数器回绕也会造成问题。
二、算法描述
一个empty bloom filter是一个有m bits的bit array,每一个bit位都初始化为0。并且定义有k个不同的hash function,每个都以uniform random distribution将元素hash到m个不同位置中的一个。在下面的介绍中n为元素数,m为布隆过滤器或哈希表的slot数,k为布隆过滤器重hash function数。
为了add一个元素,用k个hash function将它hash得到bloom filter中k个bit位,将这k个bit位置1。
为了query一个元素,即判断它是否在集合中,用k个hash function将它hash得到k个bit位。若这k bits全为1,则此元素在集合中;若其中任一位不为1,则此元素比不在集合中(因为如果在,则在add时已经把对应的k个bits位置为1)。
不允许remove元素,因为那样的话会把相应的k个bits位置为0,而其中很有可能有其他元素对应的位。因此remove会引入false negative,这是绝对不被允许的。
当k很大时,设计k个独立的hash function是不现实并且困难的。对于一个输出范围很大的hash function(例如MD5产生的128 bits数),如果不同bit位的相关性很小,则可把此输出分割为k份。或者可将k个不同的初始值(例如0,1,2, … ,k-1)结合元素,feed给一个hash function从而产生k个不同的数。
当add的元素过多时,即n/m过大时(n是元素数,m是bloom filter的bits数),会导致false positive过高,此时就需要重新组建filter,但这种情况相对少见。
三、 时间和空间上的优势
当可以承受一些误报时,布隆过滤器比其它表示集合的数据结构有着很大的空间优势。例如self-balance BST, tries, hash table或者array, chain,它们中大多数至少都要存储元素本身,对于小整数需要少量的bits,对于字符串则需要任意多的bits(tries是个例外,因为对于有相同prefixes的元素可以共享存储空间);而chain结构还需要为存储指针付出额外的代价。对于一个有1%误报率和一个最优k值的布隆过滤器来说,无论元素的类型及大小,每个元素只需要9.6 bits来存储。这个优点一部分继承自array的紧凑性,一部分来源于它的概率性。如果你认为1%的误报率太高,那么对每个元素每增加4.8 bits,我们就可将误报率降低为原来的1/10。add和query的时间复杂度都为O(k),与集合中元素的多少无关,这是其他数据结构都不能完成的。
如果可能元素范围不是很大,并且大多数都在集合中,则使用确定性的bit array远远胜过使用布隆过滤器。因为bit array对于每个可能的元素空间上只需要1 bit,add和query的时间复杂度只有O(1)。注意到这样一个哈希表(bit array)只有在忽略collision并且只存储元素是否在其中的二进制信息时,才会获得空间和时间上的优势,而在此情况下,它就有效地称为了k=1的布隆过滤器。
而当考虑到collision时,对于有m个slot的bit array或者其他哈希表(即k=1的布隆过滤器),如果想要保证1%的误判率,则这个bit array只能存储m/100个元素,因而有大量的空间被浪费,同时也会使得空间复杂度急剧上升,这显然不是space efficient的。解决的方法很简单,使用k>1的布隆过滤器,即k个hash function将每个元素改为对应于k个bits,因为误判度会降低很多,并且如果参数k和m选取得好,一半的m可被置为为1,这充分说明了布隆过滤器的space efficient性。
四、 举例说明
以垃圾邮件过滤中黑白名单为例:现有1亿个email的黑名单,每个都拥有8 bytes的指纹信息,则可能的元素范围为![]()
,对于bit array来说是根本不可能的范围,而且元素的数量(即email列表)为
![]()
,相比于元素范围过于稀疏,而且还没有考虑到哈希表中的collision问题。
若采用哈希表,由于大多数采用open addressing来解决collision,而此时的search时间复杂度为![]()
。即若哈希表半满(n/m = 1/2),则每次search需要probe 2次,因此在保证效率的情况下哈希表的存储效率最好不超过50%。此时每个元素占8 bytes,总空间为:
![]()
。若采用Perfect hashing(这里可以采用Perfect hashing是因为主要操作是search/query,而并不是add和remove),虽然保证worst-case也只有一次probe,但是空间利用率更低,一般情况下为50%,worst-case时有不到一半的概率为25%。
若采用布隆过滤器,取k=8。因为n为1亿,所以总共需要 ![]()
被置位为1,又因为在保证误判率低且k和m选取合适时,空间利用率为50%(后面会解释),所以总空间为:
![]()
。所需空间比上述哈希结构小得多,并且误判率在万分之一以下。
五、误判概率的证明和计算
假设布隆过滤器中的hash function满足simple uniform hashing假设:每个元素都等概率地hash到m个slot中的任何一个,与其它元素被hash到哪个slot无关。若m为bit数,则对某一特定bit位在一个元素由某特定hash function插入时没有被置位为1的概率为:
则k个hash function中没有一个对其置位的概率为:
如果插入了n个元素,但都未将其置位的概率为:
则此位被置位的概率为:
现在考虑query阶段,若对应某个待query元素的k bits全部置位为1,则可判定其在集合中。因此将某元素误判的概率为:
从上式中可以看出,当m增大或n减小时,都会使得误判率减小,这也符合直觉。
现在计算对于给定的m和n,k为何值时可以使得误判率最低。设误判率为k的函数为:
![]()
,两边取对数
![]()
, 两边对k求导
下面求最值
![]()
![]()
![]()
![]()
![]()
![]()
可以看出若要使得误判率≤1/2,则:
这说明了若想保持某固定误判率不变,布隆过滤器的bit数m与被add的元素数n应该是线性同步增加的。
六、设计和应用布隆过滤器的方法
应用时首先要先由用户决定要add的元素数n和希望的误差率P。这也是一个设计完整的布隆过滤器需要用户输入的仅有的两个参数,之后的所有参数将由系统计算,并由此建立布隆过滤器。
系统首先要计算需要的内存大小m bits:
再由m,n得到hash function的个数:
至此系统所需的参数已经备齐,接下来add n个元素至布隆过滤器中,再进行query。
根据公式,当k最优时:
因此可验证当P=1%时,存储每个元素需要9.6 bits:
而每当想将误判率降低为原来的1/10,则存储每个元素需要增加4.8 bits:
这里需要特别注意的是,9.6 bits/element不仅包含了被置为1的k位,还把包含了没有被置为1的一些位数。此时的
才是每个元素对应的为1的bit位数。
此概率为某bit位在插入n个元素后未被置位的概率。因此,想保持错误率低,布隆过滤器的空间使用率需为50%。
七、Bloom Filter 用例
Google 著名的分布式数据库 Bigtable 使用了布隆过滤器来查找不存在的行或列,以减少磁盘查找的IO次数[3]。
Squid 网页代理缓存服务器在 cache digests 中使用了也布隆过滤器[4]。
Venti 文档存储系统也采用布隆过滤器来检测先前存储的数据[5]。
SPIN 模型检测器也使用布隆过滤器在大规模验证问题时跟踪可达状态空间[6]。
Google Chrome浏览器使用了布隆过滤器加速安全浏览服务[7]。
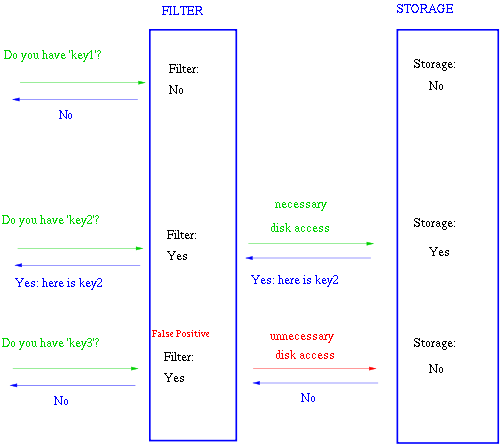
在很多Key-Value系统中也使用了布隆过滤器来加快查询过程,如 Hbase,Accumulo,Leveldb,一般而言,Value 保存在磁盘中,访问磁盘需要花费大量时间,然而使用布隆过滤器可以快速判断某个Key对应的Value是否存在,因此可以避免很多不必要的磁盘IO操作,只是引入布隆过滤器会带来一定的内存消耗,下图是在Key-Value系统中布隆过滤器的典型使用:
八、布隆过滤器相关扩展
Counting filters
基本的布隆过滤器不支持删除(Deletion)操作,但是 Counting filters 提供了一种可以不用重新构建布隆过滤器但却支持元素删除操作的方法。在Counting filters中原来的位数组中的每一位由 bit 扩展为 n-bit 计数器,实际上,基本的布隆过滤器可以看作是只有一位的计数器的Counting filters。原来的插入操作也被扩展为把 n-bit 的位计数器加1,查找操作即检查位数组非零即可,而删除操作定义为把位数组的相应位减1,但是该方法也有位的算术溢出问题,即某一位在多次删除操作后可能变成负值,所以位数组大小 m 需要充分大。另外一个问题是Counting filters不具备伸缩性,由于Counting filters不能扩展,所以需要保存的最大的元素个数需要提前知道。否则一旦插入的元素个数超过了位数组的容量,false positive的发生概率将会急剧增加。当然也有人提出了一种基于 D-left Hash 方法实现支持删除操作的布隆过滤器,同时空间效率也比Counting filters高。
Data synchronization
Byers等人提出了使用布隆过滤器近似数据同步[9]。
Bloomier filters
Chazelle 等人提出了一个通用的布隆过滤器,该布隆过滤器可以将某一值与每个已经插入的元素关联起来,并实现了一个关联数组Map[10]。与普通的布隆过滤器一样,Chazelle实现的布隆过滤器也可以达到较低的空间消耗,但同时也会产生false positive,不过,在Bloomier filter中,某 key 如果不在 map 中,false positive在会返回时会被定义出的。该Map 结构不会返回与 key 相关的在 map 中的错误的值。
在下一节,我们将会用Java 实现一个简单的 BloomFilter.
用Java实现 BloomFilter:http://blog.csdn.net/zq602316498/article/details/40660695
本文图片和内容文字来源与两篇文章,原文地址:
http://www.cnblogs.com/allensun/archive/2011/02/16/1956532.html
http://www.cnblogs.com/haippy/archive/2012/07/13/2590351.html
![【转】BloomFilter布隆滤波器 clip_image002[24]](http://img.e-com-net.com/image/info8/03605c9d1e90440faab428ac34092cc2.png)
![【转】BloomFilter布隆滤波器 clip_image002[30]](http://img.e-com-net.com/image/info8/539fec9929364699bc4e2517c0f8c2bd.png)
![【转】BloomFilter布隆滤波器 clip_image002[40]](http://img.e-com-net.com/image/info8/77650f3dd8d44bbabe08f69e63e5176d.png)