奇异值分解(SVD)原理详解及推导-矩阵相关

SVD原理以及推导

一。关于这篇文章的开始几句话

       看过我之前写过文章的童鞋们会发现我写文章的水平很烂的，所以看官们见谅啊！ SVD不仅是一个数学问题，在数学问题上主要涉及矩阵的计算，矩阵已经忘记的童鞋们最好去复习一下相关知识啊。说实话我还没怎么在实际开发中用过SVD，但是SVD以前我不会，原理和推导过程还是有意思的。

       引用一句流行语——没时间解释了，快上车！！！！

二。直接开始

        用SVD可以很容易得到 任意矩阵的满秩分解 ，用满秩分解可以对数据做压缩。可以用SVD来证明对任 意M*N的矩阵均存在如下分解：

在这里Rank(A)表示的是矩阵A的秩。看到高手写的文章中说：这个可以应用在数据降维压缩上！在数据相关性特别大的情况下存储X和Y矩阵比存储A矩阵占用空间更小！接下来我们来看看为什么一个矩阵A可以分解为X和Y，如果可以合理的分解，那么用来存储也就是情理之中啦。

1.首先补充下线性代数的知识

   （1）正交矩阵

     正交矩阵是在欧几里得空间里的叫法，在酉空间里叫酉矩阵，一个正交矩阵对应的变换叫正交变换。别问我什么是欧几里得空间！！！！

     欧几里得空间：设V是实数域R上的一个线性空间，在V上定义了一个二元实函数，称为内积，记作(A,B)，它具有一下性质：

    (A,B) =(B,A)

    (kA,B)=k(B,A)

    (A+B,T) = (A,T)+(B,T)

   (A,A) >= 0   当且仅当A=0时 (A,A) = 0

这里A，B，T是V中任意向量，k是任意实数，这样的线性空间V是欧几里得空间。

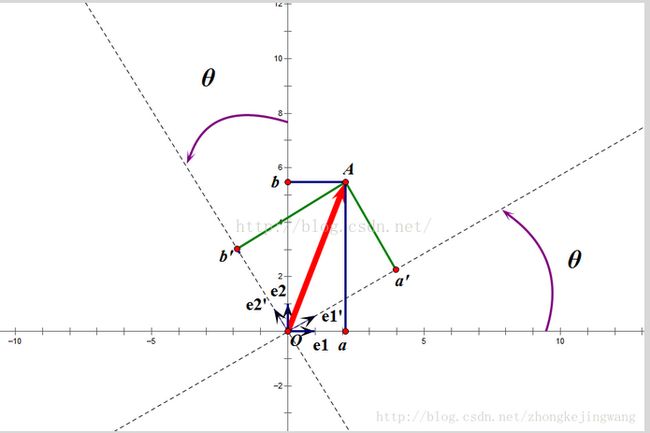
这个变换的特点是不改变向量的尺寸和向量间的夹角，那么它到底是个什么样的变换呢？看下面这张图：

假设二维空间中的一个向量OA，它在标准坐标系(即e1、e2表示的坐标系)中表示为(a,b)'（用'表示转置），如图所示，现在把向量OA用另一组坐标e1'、e2'(在e1'和e2'表示的坐标系)表示为(a',b')'，存在矩阵U使得(a',b')'=U(a,b)'，则U即为正交矩阵。

这里不必纠结于(')表示的转置。在矩阵概念里，一个矩阵的转置还是矩阵，在这里只是一个示意表明不同量(a和a‘)，并没有表示数值的不同或者相同。

设M是对称矩阵， P是正交矩阵， N=P'MP 称为 M的正交变换。

正交变换既是相似变换，也是相合变换。正交变换不改变M的特征值。正交变换既是相似变换，也是相合变换。正交变换不改变M的特征值。

从图中可以看到，正交变换只是将变换向量(OA)用另一组正交基表示，在这个过程中并没有对向量做拉伸，也不改变向量的空间位置。上面的例子只是正交变换的一个方面，即旋转变换，可以把e1'、e2'坐标系看做是e1、e2坐标系经过旋转SITA角度得到，怎么样得到这个神奇的旋转矩阵U呢？如下：

a'和b'实际上是x(就是OA啦)在e1'和e2'轴上的投影大小，所以直接做内积可得。x与e1'内积的结果就是向量 x在e1'上的投影，因为单位向量e1'的模是1啊，就是x的模乘以夹角的余弦，当然方向和e1'相同。

等式的最后面就是x*e1'的变化，结果都是相同的，同样的原因 向量e1'转置的模也是1啊。  然后:

从上面的公式可以得到：

仔细看第一张图，假如e1'和e1的夹角是SITA的话，那么就有：

所以我们可以得到：

正交阵U行（列）向量之间都是单位正交向量。

上面求得的是一个旋转矩阵，它对向量做旋转变换！也许你会有疑问：刚才不是说向量空间位置不变吗？怎么现在又说它被旋转了？对的，这两个并没有冲突，说空间位置不变是绝对的，但是坐标是相对的，加入你站在e1上看OA，随着e1旋转到e1'，看OA的位置就会改变。如下图：

如图，如果我选择了e1'、e2'作为新的标准坐标系，那么在新坐标系中OA（原标准坐标系的表示）就变成了OA'，这样看来就好像坐标系不动，把OA往顺时针方向旋转了“斯塔”角度，这个操作实现起来很简单：将变换后的向量坐标仍然表示在当前坐标系中。

总结：正交矩阵的行（列）向量都是两两正交的单位向量，正交矩阵对应的变换为正交变换，它有两种表现：旋转和反射。正交矩阵将标准正交基映射为标准正交基（即图中从e1、e2到e1'、e2'）。能力有限，我就不说反射了，我还想早点下班回家呢。

2.特征值分解——EVD

在讨论SVD之前先讨论矩阵的特征值分解（EVD），在这里，选择一种特殊的矩阵——对称阵。对称阵有一个很优美的性质：它总能相似对角化，对称阵不同特征值对应的特征向量两两正交。一个矩阵能相似对角化即说明其特征子空间即为其列空间，若不能对角化则其特征子空间为列空间的子空间。

列空间：一个由矩阵的所有的列进行线性组合而形成的空间

特征子空间:数学上,线性变换的特征向量是一个非退化的向量,其方向在该变换下不变.该向量在此变换下缩放的比例称为其特征值.一个变换通常可以由            其特征值和特征向量完全描述.特征空间是相同特征值的特征向量的集合.
特征子空间就是特征空间的符合某些条件的子空间.

现在假设存在mxm的满秩对称矩阵A，它有m个不同的特征值，设特征值为

则有以下公式：

然后有：

需要注意的是这里U是一个行向量。

所以可得到A的特征值分解（由于对称阵特征向量两两正交，所以U为正交阵，正交阵的逆矩阵等于其转置）

这里假设A有m个不同的特征值，实际上，只要A是对称阵其均有如上分解。

矩阵A分解了，相应的，其对应的映射也分解为三个映射。现在假设有x向量，用Ａ将其变换到Ａ的列空间中，那么首先由U'(U的转置)先对x做变换：

U是正交阵U'也是正交阵，所以U'对x的变换是正交变换，它将x用新的坐标系来表示，这个坐标系就是A的所有正交的特征向量构成的坐标系，因为U’对x做了正交变换而且U‘的就是A的特征向量构成的(上文已经写道)。比如将x用A的所有特征向量表示为：

上式子中x1，x2.....就是A的特征向量。

则通过第一个变换就可以把x表示为[a1 a2 ... am]'：(在A的所有正交的特征向量构成的坐标系中)

紧接着，在新的坐标系表示下，由中间那个对角矩阵对新的向量坐标换，其结果就是将向量往各个轴方向拉伸或压缩：

这里可以看做是x在新的坐标下被表示后，有m维表示x，每个维度都乘以一个数值，要么拉伸要么压缩。

从上图可以看到，如果A不是满秩的话(对角矩阵就没有个m个对角值啦)，那么就是说对角阵的对角线上元素存在0，这时候就会导致维度退化，这样就会使映射后的向量落入m维空间的子空间中。上个等式的最后就没有m个了。 

最后一个变换就是U对拉伸或压缩后的向量做变换(就是等式的最后)，由于U和U'是互为逆矩阵，所以U变换是U'变换的逆变换。 

因此，从对称阵(A)的分解对应的映射分解来分析一个矩阵的变换特点是非常直观的。假设对称阵特征值全为1那么显然它就是单位阵(A)，如果对称阵的特征值有个别是0其他全是1，那么它就是一个正交投影矩阵，它将m维向量投影到它的列空间中。 

根据对称阵A的特征向量，如果A是2*2的，那么就可以在二维平面中找到这样一个矩形，是的这个矩形经过A变换后还是矩形： 

如同上面的x经过A变换后，m个维度要么拉伸要么压缩。这个矩形的选择就是让其边都落在A的特征向量方向上，如果选择其他矩形的话变换后的图形就不是矩形了。

3.奇异值分解——SVD

上面的特征值分解的A矩阵是对称阵，根据EVD可以找到一个（超）矩形使得变换后还是（超）矩形，也即A可以将一组正交基映射到另一组正交基！那么现在来分析：对任意M*N的矩阵，能否找到一组正交基使得经过它变换后还是正交基？答案是肯定的，它就是SVD分解的精髓所在。

现在假设存在M*N矩阵A，事实上，A矩阵将n维空间中的向量映射到k（k<=m）维空间中，k=Rank(A)。现在的目标就是：在n维空间中找一组正交基，使得经过A变换后还是正交的。假设已经找到这样一组正交基：

则A矩阵将这组基映射为：

如果它们两两正交，即

根据假设，有以下等式：

所以如果正交基v选择为A'A的特征向量的话，由于A'A是对称阵，v之间两两正交，那么

这样就找到了正交基使其映射后还是正交基了，现在，将映射后的正交基单位化，因为 

vi是基向量，模长是1.所以有：

所以取单位向量

由此可得： 

当k < i <= m时，对u1，u2，...，uk进行扩展u(k+1),...,um，使得u1，u2，...，um为m维空间中的一组正交基，即

同样的，对v1，v2，...，vk进行扩展v(k+1),...,vn（这n-k个向量存在于A的零空间中，即Ax=0的解空间的基），使得v1，v2，...，vn为n维空间中的一组正交基，，正交基内积是0的。可得：

则可以得到：

继而得到：

上面的等式就是奇异值分解。

V和U含有扩展的部分，因为A不是对称矩阵，是m×n的。

现在可以来对A矩阵的映射过程进行分析了：如果在n维空间中找到一个（超）矩形，其边都落在A'A的特征向量的方向上，那么经过A变换后的形状仍然为（超）矩形！ 

vi为A'A的特征向量，称为A的右奇异向量，ui=Avi实际上为AA'的特征向量，称为A的左奇异向量。下面利用SVD证明文章一开始的满秩分解： 

注意这里的满秩是有扩展的，不是满秩的需要扩展的时候可以分解，满秩的当然也可以。

利用矩阵分块乘法展开得： 

可以看到第二项为0，有 

令

则A=XY即是A的满秩分解。文章一开始说，矩阵A被分解为X和Y其实是压缩了，存储X和Y相对于存储A来说需要更小的空间，这一点在看A X和Y的维度上分析就可以看出。所以可以做图片压缩处理。

整个SVD的推导过程就是这样。

最后说两句，这篇文章我是理解为主，是一个很好的数学思维。顺便分享以下我学习原文的地址：

http://blog.sina.com.cn/s/blog_3f738ee00102val0.html