第一章 统计学习方法概论

1.1统计学习

统计学习方法由监督学习（supervised learning）、非监督学习（unsupervised learning）、半监督学习（semi-supervised learning）和强化学习（reinforcement learning）等组成。

其中监督学习的实现步骤：
①得到一个有限的训练集合。
②得到模型的假设空间。
③确定模型的选择准则，即学习策略。
④实现求解最优模型的算法。
⑤通过学习方法选择最优模型。
⑥利用学习的最优模型对新数据进行预测或者分析。

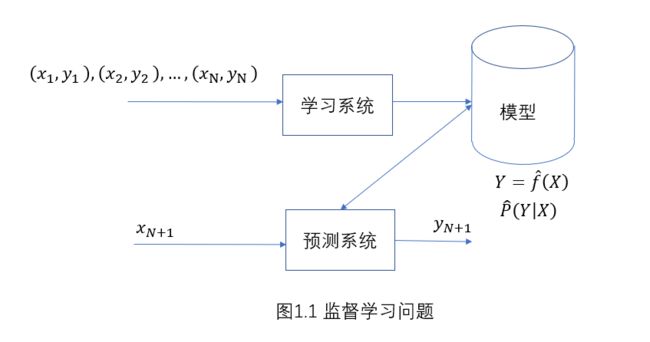
1.2监督学习

训练集：
$$T=(x_1,y_1),(x_2,y_2),...,(x_N,y_N)$$

实例$x$的特征向量：
$$x=(x^{(1)},x^{(2)},...,x^{(n)}{)}^T$$

模型：
1)决策函数$$Y=f(X)$$
预测形式$$y=f(x)$$

2)条件概率分布;$$P(Y|X)$$
预测形式$$argmaxP(y|x)$$

1.3监督学习三要素

模型（model）
策略（strategy）
算法（algorithm）

---

1.3.1模型（假设空间）：

决策函数
$$F=\{f|Y=f_{\theta }(X),\theta \in R^n\}$$
条件概率分布
$$F=\{P|P_{\theta }(Y|X),\theta \in R^n\}$$

---

1.3.2策略

常见损失函数：
$$L(Y,f(X))=\{\begin{array}{rlr}1& ,& Y̸=f(X)\\ 0& ,& Y=f(X)\end{array}$$
$$L(Y,f(X))=(Y-f(X){)}^2$$
$$L(Y,f(X))=|Y-f(X)|$$
$$L(Y,P(Y|X)=\log (P(Y|X))$$

经验风险最小化：
$$\begin{gathered} min \\ （f\in F）\frac{1}{N}\sum _{i=1}^{N}L(y_i,f(x_i)) \end{gathered}$$
结构风险最小化：
$$min(f\in F)\frac{1}{N}\sum _{i=1}^{N}L(y_i,f(x_i))+\lambda J(f)$$

---

1.3.3算法

1.4模型评估和模型选择

训练误差
$$\frac{1}{N}\sum _{i=1}^{N}L(y_i,\hat{f}(x_i))$$

测试误差
$$\frac{1}{N\prime }\sum _{i=1}^{N\prime }L(y_i,\hat{f}(x_i))$$

Markdown码公式真心累~o(╥﹏╥)o