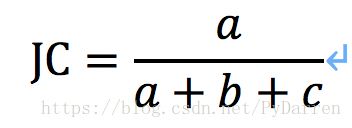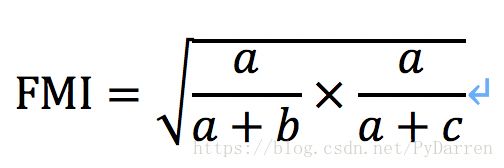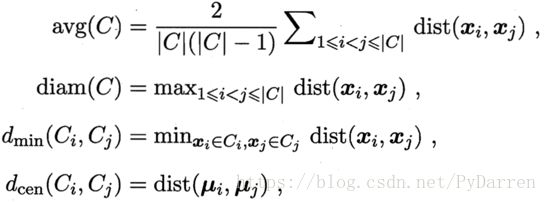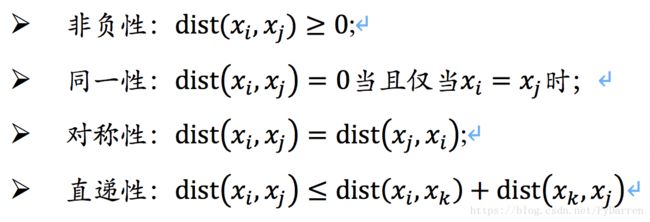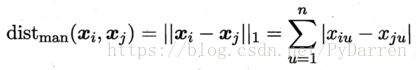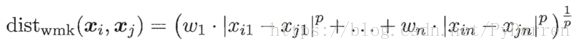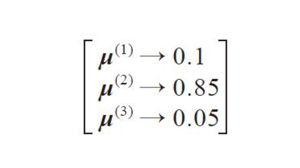十大机器学习方法之聚类分析
聚类分析是一种无监督学习技术(常见的无监督学习还有密度估计、异常检测等),可以在事先不知道正确结果(即无类标或预期输出值)的情况下,发现数据本身所蕴含的结构信息。其目标是发现数据中自然形成的分组,使得每个簇内样本的相似性大于其他簇内样本的相似性。聚类的商业领域应用包括:按照不同主题对文档、音乐、电影进行分组,或基于常见的购买行为,发现有相同兴趣爱好的顾客,并以此构建推荐引擎。
聚类既可以作为一个单独的过程,用于寻找数据中内在的分布结构,也可以作为分类等其他任务的前驱过程。
一、性能度量
大致分为两类:一类是将聚类结果与某种参考模型(例如将某领域专家给出的分类结果作为参考模型)进行比较,称为外部指标;另一类是直接考察外部结果而不利用任何参考模型,称为内部指标。
其中带*的为参考模型的结果。
常用的聚类性能外部指标:
- Jaccard系数(JC)
- FM指数(FowlkesandMallowsIndex,简称FMI)
- Rand指数(RI)
显然上述指标大小都在[0,1]之间,且距离越大越好。
考虑聚类结果的簇划分,定义:
其中,dist(.,.)代表两者之间的距离;代表该簇的中心点;avg(C)表示簇C内样本间的平均距离;diam(C)代表簇C内样本之间的最远距离;dmin(Ci,Cj)代表簇Ci与簇Cj最近样本之间的距离;dcen(Ci,Cj) 代表簇Ci与簇Cj中心点之间的距离。
常用的聚类内部衡量指标:
显然,DBI的值越小越好;DI则相反,其值越大越好。
二、距离计算
通常情况下,距离应满足四个性质(不一定同时都满足的):
给定样本xi=(xi1,xi2,…,xin)与xj=(xj1,xj2,…,xjn),最常用的是闵可夫斯基距离(可用于有序属性):
当p=2时,即为欧氏距离:
当p=1时,即为曼哈顿距离:
当属性的相对重要性不同时,可以使用“加权距离”:
对于无序属性可采用VDM(Value Difference Metric)来计算:
其中mu,a表示属性u上取值为a的样本数;mu,a,i表示在第i个簇中属性u上取值为a的样本数。
将闵可夫斯基距离和VDM结合可以处理混合属性:
三、K-means算法
K-means算法由于易于实现,并且具有很高的计算效率,在学术领域及业界得到了广泛应用。K-means算法是基于原型的聚类(假设聚类结构能通过一组原型刻画),意味着每个簇都对应着一个原型,它可以是一些具有连续型特征的相似点的中心点(平均值),或者是类别特征情况下相似点的众数——最典型或者出现频率最高的点;缺点是需要事前指定簇的数量k,如果k值选择不当,则导致聚类效果不佳或产生收敛速度慢等问题。
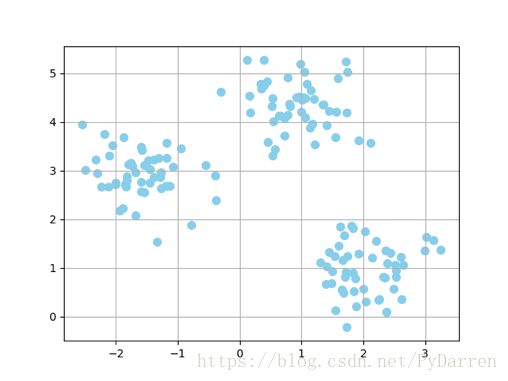
1. from sklearn.datasets import make_blobs
2. X,y = make_blobs(n_samples=150, n_features=2, centers=3, cluster_std=0.5, shuffle=True, random_state=0)
3. import matplotlib.pyplot as plt
4. plt.scatter(X[:,0], X[:,1], c='skyblue', marker='o', s=50)
5. plt.grid()
6. plt.show()
算法步骤:
- 从样本点中随机选取k个点作为初始簇中心;
- 将每个样本点划分到距离它最近到中心点所代表的簇中;
- 用各簇中所有样本的中心点替代原有的中心点;
- 重复步骤2和3,直到中心点不变或者达到预定迭代次数,算法终止。
常用的距离度量指标——欧几里得距离的平方:
通过迭代使得簇内误差平方和(SSE)最小,也称作簇惯性;
其中为簇j的中心点,如果样本属于簇j,则,否则为零。
1. from sklearn.cluster import KMeans
2. km = KMeans(n_clusters=3,
3. init='random',
4. n_init=10,
5. max_iter=300,
6. tol=1e-04,
7. random_state=0)
8. y_km = km.fit_predict(X)
二、K-means++算法
前面的K-means算法使用随机点作为中心点,若中心点选择不当,会导致簇分类不佳或收敛速度慢。解决这一问题的一种方法是在数据集上多次运行K-means算法,并根据误差平方和(SSE)选择最优模型。另一种方法就是使用K-means++算法使得初始中心点尽可能的远。
- 算法过程:
- 初始化一个集合M,用来存储选定的k个中心点;
- 从输入样本中随机选择一个中心点,将其添加到集合M中;
- 对于集合M之外的任一样本点,通过计算找到与其平方距离最小的的样本;
- 使用加权概率分布来随机选择下一个中心点;
- 重复步骤2、3,直到选择k个中心点;
- 基于选定的中心点执行k-means算法。
Sklearn中实现k-means++只需将init参数值的random替换为k-means++即可。
1. #可视化展示结果
2. cl_list = (0,1,2)
3. colors_list = ('red','grey','green')
4. markers_list = ('o','x','^')
5.
6. for cl,color,marker in zip(cl_list,colors_list,markers_list):
7. plt.scatter(X[y_km==cl,0],
8. X[y_km==cl,1],
9. s=50,
10. c=color,
11. marker=marker,
12. label="cluster {}".format(cl))
13.
14. plt.scatter(km.cluster_centers_[:,0],
15. km.cluster_centers_[:,1],
16. s=250,
17. marker='*',
18. c='black',
19. label='centroids')
20. plt.legend(loc='best')
21. plt.grid()
22. plt.savefig("/Users/chenda/Desktop/1.png")
23. plt.show()
三、硬聚类和软聚类
硬聚类是指数据集中每个样本只能划分到一个簇的算法,例如k-means算法。软聚类(模糊聚类)是指算法可以将一个样本划分到一个或者多个簇。一个常见的算法是模糊C-means(FCM)算法,其处理过程与k-means类似,但是使用每个样本点隶属于各簇的概率来替代硬聚类的划分。
每个值都在区间[0,1]内,代表样本属于相应簇的概率,各概率之和为1。实际应用中k-means算法和FCM算法通常会得到较为相似的距离。