史上最简单的python算法入门书,像看小说一样学习算法你敢信?
算法是计算机科学领域最重要的基石之一,同时也是出了名地难学。最出名的一本书莫过于算法导论了
但是,这本非常非常出名的大头书,真的是谁看谁知道。看了之后都有点怀疑人生,一大批人也因此从入门到放弃。
但是还是有很多人跑去学算法,为什么呢?
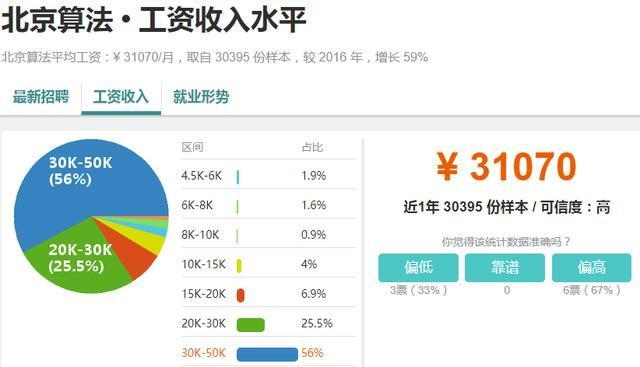
原因还是算法工程师的待遇实在是太好了,做技术岗位的都能达到月薪三万,如果再会点业务做管理呢?想都不敢想哦。
其实算法真的难吗?其实不然。如果你觉得难得话,那肯定是因为你没有看过这本书
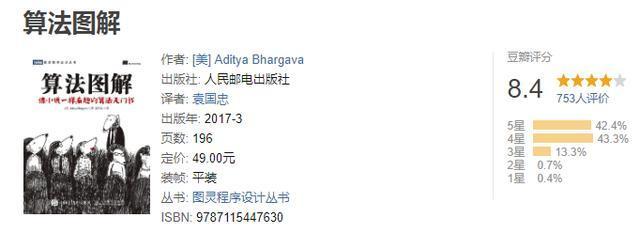
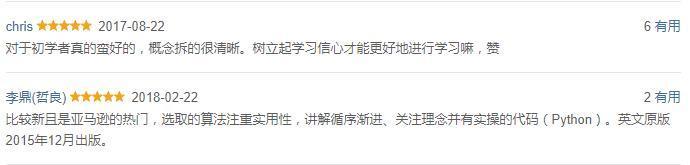
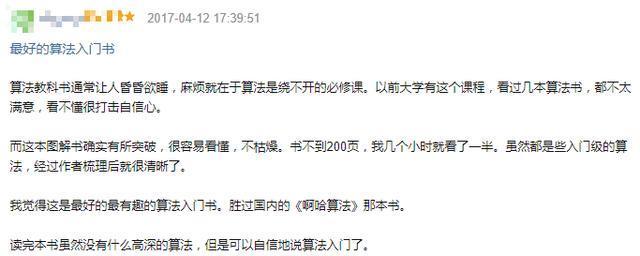
号称能像看小说一样看懂算法。我一开始也是不信的,毕竟我可是看过算法导论的人。因为是图灵出版社(国内最好的IT类书籍出版社)出版的书籍,所以我还是买来看了一下,结果就真的就像是看小说一样,花了一天时间全部看完了。我们也可以看一下别人的评论。
我自己是看过这本书的,所以我对上面的评论也深信不疑。由于好评太多了,我就不一一展示了,想要详细了解的可以去看一下豆瓣评论。接下来我们看一下部分内容。
内容部分
一、算法简介
1.1二分查找 :
一个有序数组中找一个数的位置(对应该数字所在数组下标index)。
def binary_search(list, item):
low = 0
high = len(list) - 1
while low <= high:
mid = int((low + high) / 2)
guess = list[mid]
if guess == item:
return mid
if guess > item:
high = mid - 1
else:
low = mid + 1
return None
my_list = [1, 3, 5, 7, 9]
print(binary_search(my_list, 3)) # => 1
print(binary_search(my_list, -1)) # => None
也可用递归实现
操作对象:数组
使用前提:有序的数组
性能方面:时间复杂度O(logn)
1.2 旅行商问题:
旅行商前往n个城市,确保旅程最短。求可能的排序:n!种可能。
二、选择排序
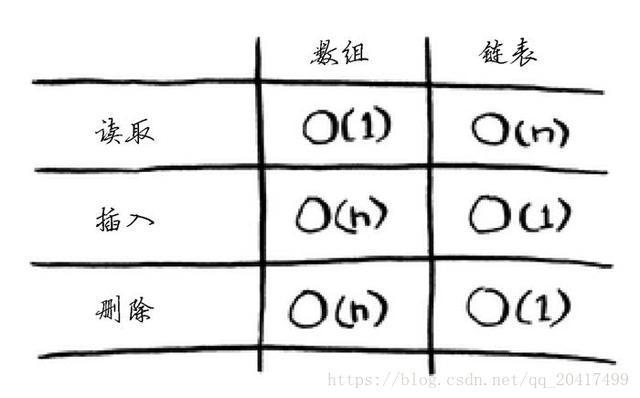
2.1 数组和链表
数组:连续存储在硬盘中;链表:分散存储在硬盘中;
2.2 选择排序:将数组元素按照从小到大的顺序排序,每次从数组中取出最小值
def findSmallest(arr):
smallest = arr[0]
smallest_index = 0
for i in range(1, len(arr)):
if arr[i] < smallest:
smallest = arr[i]
smallest_index = i
return smallest_index
def selectionSort(arr):
newArr = []
for i in range(len(arr)):
smallest = findSmallest(arr)
newArr.append(arr.pop(smallest))
return newArr
print(selectionSort([5, 3, 6, 2, 10])) #[2, 3, 5, 6, 10]
三、递归----一种优雅的问题解决方法
适用递归的算法要满足:
基限条件(即返回的条件)
递归条件(调用递归函数)
特点:
自己调用自己,调用栈在内存叠加,如果没有返回条件,将无限循环调用,占用大量内存,最终爆栈终止进程。
还有一种高级一点的递归:
尾递归 (将结果也放入函数参数,内存里面调用栈只有一个当前运行的函数进程)
举个简单的例子: 阶乘f(n) = n!
def fact(x): #递归
if x == 1:
return 1
else:
return x * fact(x-1) #注意这里跟尾递归不同
#尾递归
def factorial(x,result):
if x == 1:
return result
else:
return factorial(x-1,x*result)
if __name__ == '__main__':
print(fact(5)) #5*4*3*2*1 = 120
print(factorial(5,1)) #120
四、快速排序 (分而治之策略)
每次选取数组中一个元素x当作分水岭(一般选取第一个元素):[小于元素x的数组]+[x]+[大于元素x的数组],然后递归调用,直到最后处理的数组元素只剩下零个或者一个
平均时间复杂度O(nlogn)
最差情况时间复杂度O(n^2) (出现这个情况是:快排的数组本来就是有序的(顺序/倒序),选取的元素又是开头第一个的话,每次变成只能处理一侧的数组了。 改善:可以选取数组中间的元素当作分水岭pivot,只有两边的元素就都能均匀处理了)
#!/usr/bin/python
def quicksort(array):
if len(array) < 2:
return array
else:
pivot = array[0]
less = [i for i in array[1:] if i <= pivot] #超级像伪代码!
print(less)
greater = [i for i in array[1:] if i > pivot]
print(greater)
return quicksort(less) + [pivot] + quicksort(greater)
if __name__ == '__main__':
print(quicksort([7,1,10,5,3,2,6]))
'''
[1, 5, 3, 2, 6]
[10]
[]
[5, 3, 2, 6]
[3, 2]
[6]
[2]
[]
[1, 2, 3, 5, 6, 7, 10]
'''
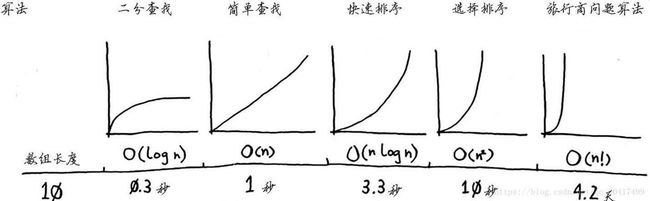
到目前算法为止,复杂度对比:
排序到算法有:
冒泡排序,选择排序,快速排序,归并排序,堆排序(感兴趣到小伙伴可以自己去搜索)
下面列出冒泡排序和归并排序算法:
#冒泡排序,每次寻找最小到元素往前排,就像汽水从下往上冒一样。所以叫冒泡排序啦
def simpleSort(array):
for i in range(len(array)-1):
for j in range(i,len(array)):
if array[i] > array[j]:
temp = array[i]
array[i] = array[j]
array[j] = temp
return array
print(simpleSort([9,8,6,7,4,5,3,11,2])) #[2, 3, 4, 5, 6, 7, 8, 9, 11]
冒泡排序时间复杂度O(n^2)
两个for循环搞定,每一轮for循环找到一个最小值。for循环两两元素对比交换
归并排序:
def mergeSort(array):
if len(array) < 2:
return array
else:
mid = int(len(array)/2)
left = mergeSort(array[:mid])
right = mergeSort(array[mid:])
return merge(left, right)
def merge(left, right): #并两个已排序好的列表,产生一个新的已排序好的列表
result = [] # 新的已排序好的列表
i = 0 # 下标
j = 0
# 对两个列表中的元素 两两对比
# 将最小的元素,放到result中,并对当前列表下标加1
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
# 此时left或者right其中一个已经添加完毕,剩下的就全部加到result后面即可
result += left[i:]
result += right[j:]
return result
array = [9,5,3,0,6,2,7,1,4,8]
result = mergeSort(array)
print('排序后:',result) #排序后: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
归并排序时间复杂度是O(nlogn)
最坏情况也是O(nlogn)
后面还有很多,我就不一一列举了。这本书将深奥的知识用通俗易懂的语言表达出来,同时加上生动形象的配图,看了的都说好。
最后,学习Python中的小伙伴,需要学习资料的话,可以前往我的微信公众号:速学Python,后台回复:csdn,即可拿Python学习资料
这里有我自己整理了一套最新的python系统学习教程,包括从基础的python脚本到web开发、爬虫、数据分析、数据可视化、机器学习等。送给正在学习python的小伙伴!这里是python学习者聚集地,欢迎初学和进阶中的小伙伴!