Bp神经网络+C++实现

0 前言

　　神经网络在我印象中一直比较神秘，正好最近学习了神经网络，特别是对Bp神经网络有了比较深入的了解，因此，总结以下心得，希望对后来者有所帮助。
　　神经网络在机器学习中应用比较广泛，比如函数逼近，模式识别，分类，数据压缩，数据挖掘等领域。神经网络本身是一个比较庞大的概念，从网络结构类别来划分，大概有：多层前馈神经网络、径向基函数网络（RBF）、自适应谐振理论网络（ART）、自组织映射网络（SOM）、级联相关网络、Elman网络、Boltzmann机、受限Boltzmann机等等。
　下面一张图是最近比较流行的网络结构：

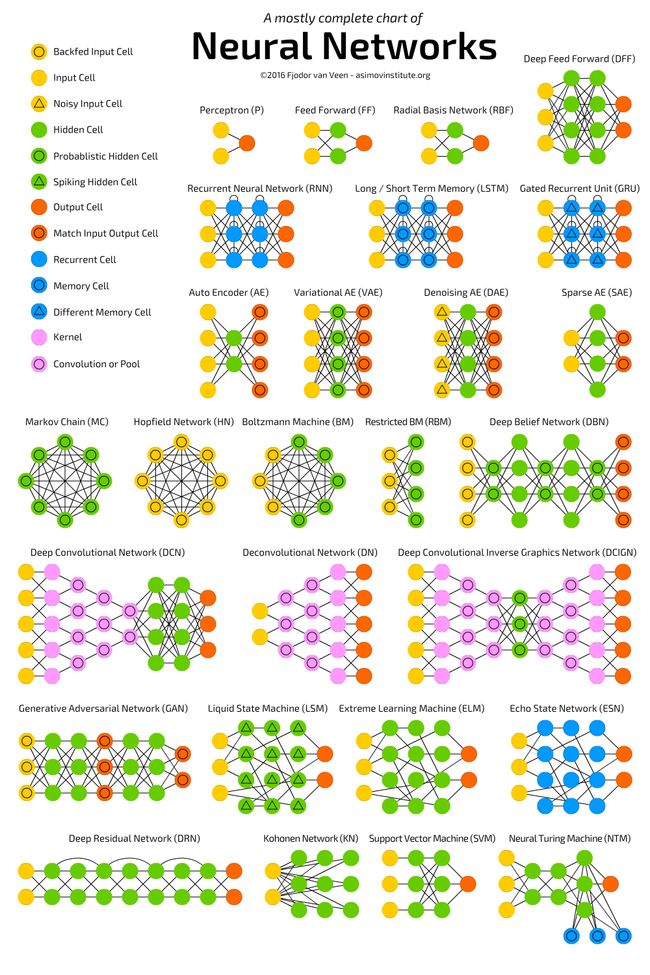
　 今天我们要介绍的是Bp神经网络，准确的说是采用Bp算法进行训练的多层前馈神经网络，Bp算法应用比较广泛。

1基本概念：

1.1神经元模型

 机器学习中所谈论的神经网络源于生物上的神经网络，实际上指的是“神经网络“与”机器学习“的交叉部分，一个最简单的M-P神经元模型如下图所示：

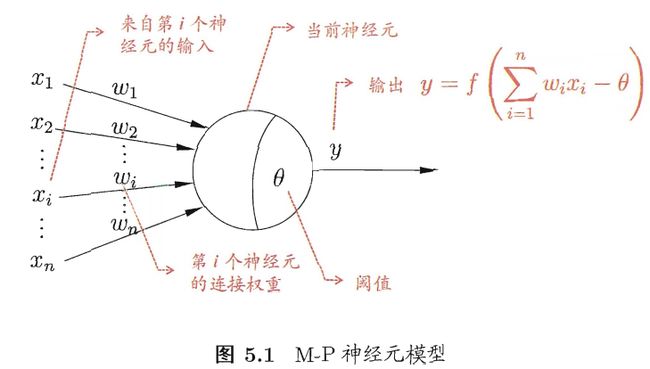
该神经元收到来自其他n个输入神经元传递过来的输入信号（加权和的形式），然后将其与神经元的阈值进行比较，通过激活函数进行处理，产生神经元的输出。

1.2 常用激活函数

激活函数的作用是对其他所有神经元传过来的所有信号加权和进行处理，产生神经元输出。

　 下图是常用的激活函数，最简单的是：阶跃函数，它简单，最理想，但是性质最差（不连续/不光滑），因此在实际中，最常用的是Sigmoid函数。

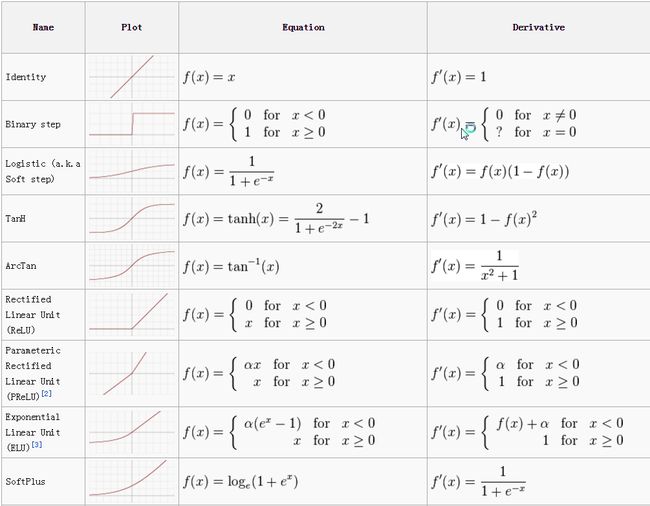
1.3前馈神经网络

   多层前馈神经网络的准确定义：每一层神经元与下一层神经元全互连，神经元之间不存在同层连接，不存在跨层连接，如下图所示就是一个经典的前馈神经网络，

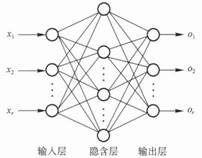
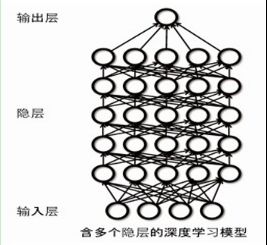
（随便插一句，当神经网络中隐层数越来越多，达到8-9层时，就变成了一个深度
学习模型，我曾在一篇论文中看到网络结构有达128层的，关于下面这块，下面还会再叙述）。

2.标准Bp算法

---

2.0 关于梯度

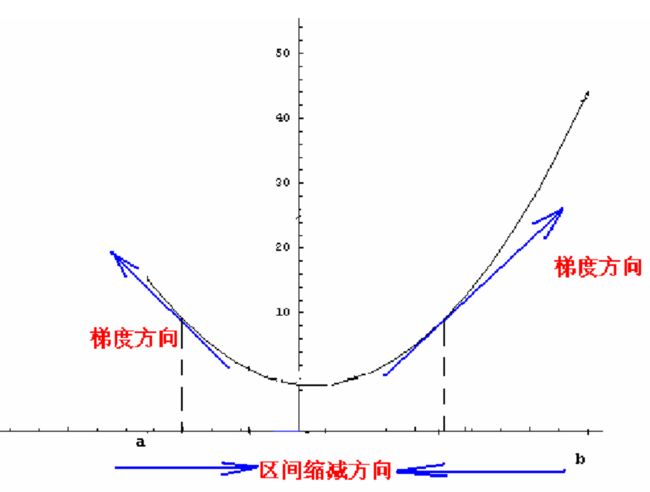
   首先我们应该清楚，一个多元函数的梯度方向是该函数值增大最陡的方向。具体化到1元函数中时，梯度方向首先是沿着曲线的切线的，然后取切线向上增长的方向为梯度方向，2元或者多元函数中，梯度向量为函数值f对每个变量的导数，该向量的方向就是梯度的方向，当然向量的大小也就是梯度的大小。
   梯度下降法(steepest descend method)用来求解表达式最大或者最小值的，属于无约束优化问题。梯度下降法的基本思想还是挺简单的，现假设我们要求函数f的最小值，首先得选取一个初始点后，然后下一个点的产生时是沿着梯度直线方向，这里是沿着梯度的反方向(因为求的是最小值，如果是求最大值的话则沿梯度的正方向即可)，如下图所示： 

---

2.1神经网络学习过程

　神经网络在外界输入样本的刺激下不断改变网络的连接权值,以使网络的输出不断地接近期望的输出，讲几个要点：
（1）学习过程可以简述为：
（2）学习的本质： 对各连接权值以及所有功能神经元的阈值动态调整
注：可以将权值与阈值的学习统一为权值的学习，即将阈值看成一个”哑节点“，如下图所示：

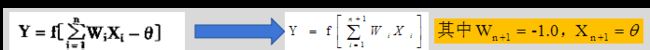
（3） 权值调整规则：即在学习过程中网络中各神经元的连接权变化所依据的一定的调整规则 ，（Bp 算法中权值调整采用的是梯度下降策略，下面会详细介绍）
Bp网络的学习流程如下图所示：

（百度图库里搜的，能说明问题就行）

---

2.2权值调整策略：

　　首先说明一句，神经网络学习属于监督学习的范畴。每输入一个样本,进行正向传播（输入层→隐层→输出层），得到输出结果以后,计算误差，达不到期望后，将误差进行反向传播（输出层→隐层→输入层），采用梯度下降策略对所有权值和阈值进行调整。

注：上面的Ek是根据第k个样本数据算出的误差，可以看出：标准Bp算法每次迭代更新只针对单个样例。
权值与阈值的调整公式如下：

上述公式的详细推导过程见下图：

---

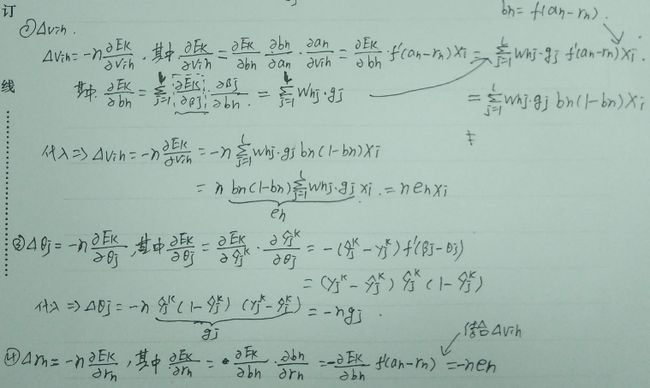
2.3 BP神经网络总结

（1）BP神经网络一般用于分类或者逼近问题。
如果用于分类，则激活函数一般选用Sigmoid函数或者硬极限函数，如果用于函数逼近，则输出层节点用线性函数。
（2） BP神经网络在训练数据时可以采用增量学习或者批量学习。
—增量学习要求输入模式要有足够的随机性，对输入模式的噪声比较敏感，即对于剧烈变化的输入模式，训练效果比较差，适合在线处理。
—批量学习不存在输入模式次序问题，稳定性好，但是只适合离线处理。
（3）如何确定隐层数以及每个隐含层节点个数
Pre隐含层节点个数不确定，那么应该设置为多少才合适呢（隐含层节点个数的多少对神经网络的性能是有影响的）？
有一个经验公式可以确定隐含层节点数目： ，（其中h:隐含层节点数目，m:为输入层节点数目，n:为输出层节点数目，a:为之间的调节常数）。

---

2.4 标准BP神经网络的缺陷

（1）容易形成局部极小值而得不到全局最优值。
（采用梯度下降法），如果仅有一个局部极小值=>全局最小，多个局部极小=>不一定全局最小。这就要求对初始权值和阀值有要求，要使得初始权值和阀值随机性足够好，可以多次随机来实现。
（2）训练次数多使得学习效率低，收敛速度慢。
每次更新只针对单个样本；不同样例出现”抵消“现象。
（3）过拟合问题
通过不断训练，训练误差达到很低，但测试误差可能会上升（泛化性能差）。
解决策略：
1，”早停”：
即将样本划分成训练集和验证集，训练集用来算梯度，更新权值和阈值，验证集用来估计误差，当训练集误差降低而验证集误差升高时就停止训练，返回具有最小验证集误差的权值和阈值。
2，”正则化方法“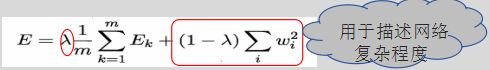：，即在误差目标中增加一个用于描述网络复杂程度的部分，其中参数λ常用交叉验证来确定。

---

2.5 BP算法的改进

（1）累积BP算法
目的：为了减小整个训练集的全局误差，而不针对某一特定样本
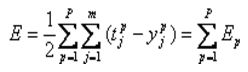（更新策略做相应调整）

（2）利用动量法改进BP算法
（标准Bp学习过程易震荡，收敛速度慢）
增加动量项，引入动量项是为了加速算法收敛，即如下公式：

α为动量系数，通常0＜α＜0.9。

（3）自适应调节学习率η
调整的基本指导思想是：在学习收敛的情况下，增大η，以缩短学习时间；当η偏大致使不能收敛（即发生震荡）时，要及时减小η，直到收敛为止。

---

3 工程搭建与C++实现

　实验平台：vs2013
项目包含文件：

项目流程如下图所示：

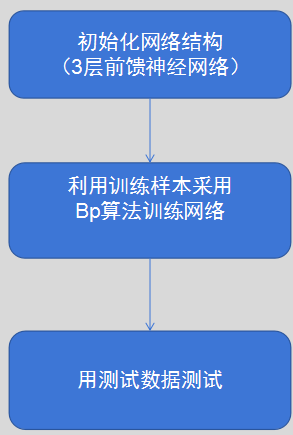
（1）Bp.h

#ifndef _BP_H_  
#define _BP_H_  

#include   

//参数设置
#define LAYER    3        //三层神经网络  
#define NUM      10       //每层的最多节点数  

#define A        30.0  
#define B        10.0     //A和B是S型函数的参数  
#define ITERS    1000     //最大训练次数  
#define ETA_W    0.0035   //权值调整率  
#define ETA_B    0.001    //阀值调整率  
#define ERROR    0.002    //单个样本允许的误差  
#define ACCU     0.005    //每次迭代允许的误差  

//类型
#define Type double  
#define Vector std::vector  

struct Data
{
    Vector x;       //输入属性
    Vector y;       //输出属性
};

class BP{

public:

    void GetData(const Vector);
    void Train();
    Vector ForeCast(const Vector);
    void ForCastFromFile(BP * &);
    void ReadFile(const char * InutFileName,int m, int n);

    void ReadTestFile(const char * InputFileName, int m, int n);
    void WriteToFile(const char * OutPutFileName);

private:

    void InitNetWork();         //初始化网络  
    void GetNums();             //获取输入、输出和隐含层节点数  
    void ForwardTransfer();     //正向传播子过程  
    void ReverseTransfer(int);  //逆向传播子过程  
    void CalcDelta(int);        //计算w和b的调整量  
    void UpdateNetWork();       //更新权值和阀值  
    Type GetError(int);         //计算单个样本的误差  
    Type GetAccu();             //计算所有样本的精度  
    Type Sigmoid(const Type);   //计算Sigmoid的值  
    void split(char *buffer, Vector &vec);

private:
    int in_num;                 //输入层节点数  
    int ou_num;                 //输出层节点数  
    int hd_num;                 //隐含层节点数  

    Vector data;            //样本数据
    Vector> testdata;//测试数据
    Vector> result;  //测试结果
    int        rowLen;            //样本数量
    int        restrowLen;        //测试样本数量

    Type w[LAYER][NUM][NUM];    //BP网络的权值  
    Type b[LAYER][NUM];         //BP网络节点的阀值  

    Type x[LAYER][NUM];         //每个神经元的值经S型函数转化后的输出值，输入层就为原值  
    Type d[LAYER][NUM];         //记录delta学习规则中delta的值,使用delta规则来调整联接权重 Wij(t+1)=Wij(t)+α(Yj-Aj(t))Oi(t)
};

#endif  //_BP_H_  

(2)Bp.cpp

#include   
#include   
#include   
#include   
#include 
#include 
#include 
using namespace std;

#include "Bp.h"  

//获取训练所有样本数据  
void BP::GetData(const Vector _data)
{
    data = _data;
}

void BP::split(char *buffer, Vector &vec)
{
    char *p = strtok(buffer, " ,");      //\t
    while (p != NULL)
    {
        vec.push_back(atof(p));
        p = strtok(NULL, " \n");
    }
}


void BP::ReadFile(const char * InutFileName, int m ,int n)
{
    FILE *pFile;
    //Test
    //pFile = fopen("D:\\testSet.txt", "r");

    pFile = fopen(InutFileName, "r");

    if (!pFile)
    {
        printf("open file %s failed...\n", InutFileName);
        exit(0);
    }

    //init dataSet  
    char *buffer = new char[100];
    Vector temp;

    while (fgets(buffer, 100, pFile))
    {
        Data t;
        temp.clear();
        split(buffer, temp);
        //data[x].push_back(temp);

        for (int i = 0; i < temp.size(); i++)
        {
            if (i < m)
                t.x.push_back(temp[i]);
            else
                t.y.push_back(temp[i]);
        }
        data.push_back(t);
    }
    //init rowLen   
    rowLen = data.size();
}

void BP::ReadTestFile(const char * InputFileName, int m, int n)
{
    FILE *pFile;

    pFile = fopen(InputFileName, "r");
    if (!pFile)
    {
        printf("open file %s failed...\n", InputFileName);
        exit(0);
    }

    //init dataSet  
    char *buffer = new char[100];
    Vector temp;

    while (fgets(buffer, 100, pFile))
    {
        Vector t;
        temp.clear();
        split(buffer, temp);
        for (int i = 0; i < temp.size(); i++)
        {
            t.push_back(temp[i]);
        }
        testdata.push_back(t);
    }

    restrowLen = testdata.size();
}

void BP::WriteToFile(const char * OutPutFileName)
{
    ofstream fout;
    fout.open(OutPutFileName);
    if (!fout)
    {
        cout << "file result.txt  open failed" << endl;
        exit(0);
    }

    Vector> ::iterator it = testdata.begin();
    Vector>::iterator itx = result.begin();
    while (it != testdata.end())  
    {    
        Vector ::iterator itt = (*it).begin();
        Vector ::iterator ittx = (*itx).begin();
        while (itt != (*it).end())
        {
             fout << (*itt) << ",";
             itt++;
        }
        fout << "\t";
        while (ittx != (*itx).end())
        {
            fout << (*ittx) << ",";
            ittx++;
        }
        it++;
        itx++;
        fout << "\n";
    }
}

//开始进行训练  
void BP::Train()
{
    printf("Begin to train BP NetWork!\n");
    GetNums();
    InitNetWork();
    int num = data.size();

    for (int iter = 0; iter <= ITERS; iter++)
    {
        for (int cnt = 0; cnt < num; cnt++)
        {
            //第一层输入节点赋值  
            for (int i = 0; i < in_num; i++)
                x[0][i] = data.at(cnt).x[i];

            while (1)
            {
                ForwardTransfer();
                if (GetError(cnt) < ERROR)    //如果误差比较小，则针对单个样本跳出循环  
                    break;
                ReverseTransfer(cnt);
            }
        }
        printf("This is the %d th trainning NetWork !\n", iter);

        Type accu = GetAccu();               //每一轮学习的均方误差E
        printf("All Samples Accuracy is %lf\n", accu);
        if (accu < ACCU) break;
    }
    printf("The BP NetWork train End!\n");
}

//根据训练好的网络来预测输出值  
Vector BP::ForeCast(const Vector data)
{
    int n = data.size();
    assert(n == in_num);
    for (int i = 0; i < in_num; i++)
        x[0][i] = data[i];

    ForwardTransfer();
    Vector v;
    for (int i = 0; i < ou_num; i++)
        v.push_back(x[2][i]);
    return v;
}

void  BP::ForCastFromFile(BP * &pBp)
{   

    Vector> ::iterator it = testdata.begin();
    Vector ou;
    while (it != testdata.end())
    {
        ou = pBp->ForeCast(*it);
        result.push_back(ou);

        it++;
    }

}

//获取网络节点数  
void BP::GetNums()
{
    in_num = data[0].x.size();                         //获取输入层节点数  
    ou_num = data[0].y.size();                         //获取输出层节点数  
    hd_num = (int)sqrt((in_num + ou_num) * 1.0) + 5;   //获取隐含层节点数    
    if (hd_num > NUM) hd_num = NUM;                     //隐含层数目不能超过最大设置  
}

//初始化网络  
void BP::InitNetWork()
{
    memset(w, 0, sizeof(w));      //初始化权值和阀值为0，也可以初始化随机值  
    memset(b, 0, sizeof(b));
}

//工作信号正向传递子过程  
void BP::ForwardTransfer()
{
    //计算隐含层各个节点的输出值  
    for (int j = 0; j < hd_num; j++)
    {
        Type t = 0;
        for (int i = 0; i < in_num; i++)
            t += w[1][i][j] * x[0][i];
        t += b[1][j];
        x[1][j] = Sigmoid(t);
    }

    //计算输出层各节点的输出值  
    for (int j = 0; j < ou_num; j++)
    {
        Type t = 0;
        for (int i = 0; i < hd_num; i++)
            t += w[2][i][j] * x[1][i];
        t += b[2][j];
        x[2][j] = Sigmoid(t);
    }
}

//计算单个样本的误差  
Type BP::GetError(int cnt)
{
    Type ans = 0;
    for (int i = 0; i < ou_num; i++)
        ans += 0.5 * (x[2][i] - data.at(cnt).y[i]) * (x[2][i] - data.at(cnt).y[i]);
    return ans;
}

//误差信号反向传递子过程  
void BP::ReverseTransfer(int cnt)
{
    CalcDelta(cnt);
    UpdateNetWork();
}

//计算所有样本的精度  
Type BP::GetAccu()
{
    Type ans = 0;
    int num = data.size();
    for (int i = 0; i < num; i++)
    {
        int m = data.at(i).x.size();
        for (int j = 0; j < m; j++)
            x[0][j] = data.at(i).x[j];
        ForwardTransfer();
        int n = data.at(i).y.size(); //样本输出的维度
        for (int j = 0; j < n; j++)
            ans += 0.5 * (x[2][j] - data.at(i).y[j]) * (x[2][j] - data.at(i).y[j]);//对第i个样本算均方误差
    }
    return ans / num;
}

//计算调整量  
void BP::CalcDelta(int cnt)
{
    //计算输出层的delta值  
    for (int i = 0; i < ou_num; i++)
        d[2][i] = (x[2][i] - data.at(cnt).y[i]) * x[2][i] * (A - x[2][i]) / (A * B);
    //计算隐含层的delta值  
    for (int i = 0; i < hd_num; i++)
    {
        Type t = 0;
        for (int j = 0; j < ou_num; j++)
            t += w[2][i][j] * d[2][j];
        d[1][i] = t * x[1][i] * (A - x[1][i]) / (A * B);
    }
}

//根据计算出的调整量对BP网络进行调整  
void BP::UpdateNetWork()
{
    //隐含层和输出层之间权值和阀值调整  
    for (int i = 0; i < hd_num; i++)
    {
        for (int j = 0; j < ou_num; j++)
            w[2][i][j] -= ETA_W * d[2][j] * x[1][i];
    }
    for (int i = 0; i < ou_num; i++)
        b[2][i] -= ETA_B * d[2][i];

    //输入层和隐含层之间权值和阀值调整  
    for (int i = 0; i < in_num; i++)
    {
        for (int j = 0; j < hd_num; j++)
            w[1][i][j] -= ETA_W * d[1][j] * x[0][i];
    }
    for (int i = 0; i < hd_num; i++)
        b[1][i] -= ETA_B * d[1][i];
}

//计算Sigmoid函数的值  
Type BP::Sigmoid(const Type x)
{
    return A / (1 + exp(-x / B));
}

(3)Test.cpp

#include   
#include   
#include   
using namespace std;

#include "Bp.h"  

int main()
{
    unsigned int Id, Od;    //样本数据的输入维数/输出维数
    int select = 0;
    BP *bp = new BP();
    const char * inputDataName = "exercisedata.txt";//训练数据文件名称
    const char * testDataName = "testdata.txt";   //测试数据文件名称
    const char * outputDataName = "result.txt";     //输出文件名称

    printf("please input sample input dimension and output dimension:\n");
    scanf("%d%d", &Id, &Od);
    bp->ReadFile(inputDataName,Id,Od);

    //exercise
    bp->Train();
    //Test
    printf("\n******************************************************\n");
    printf("*1.使用测试文件中国的数据测试 2.从控制台输入数据测试  \n");
    printf("******************************************************\n");
    scanf("%d", &select);
    switch (select)
    {
    case 1:
        bp->ReadTestFile(testDataName,Id,Od);
        bp->ForCastFromFile(bp);
        bp->WriteToFile(outputDataName);
        printf("the result have been save in the file :result.txt.\n");
        break;
    case 2:
        printf("\n\nplease input the Test Data(3 dimension )：\n");
        while (1)
        {
            Vector in;
            for (int i = 0; i < Id; i++)
            {
                Type v;
                scanf_s("%lf", &v);
                in.push_back(v);
            }
            Vector ou;
            ou = bp->ForeCast(in);
            printf("%lf\n", ou[0]);
        }
        break;
    default:
        printf("Input error!");
        exit(0);
    }

    return 0;
}