atan2与极坐标
高等数学这门课程对极坐标有过介绍,可以用下图来说明其含义,当然,有的文献将下图中角度的范围定义为半开半闭区间(-pi, pi]。
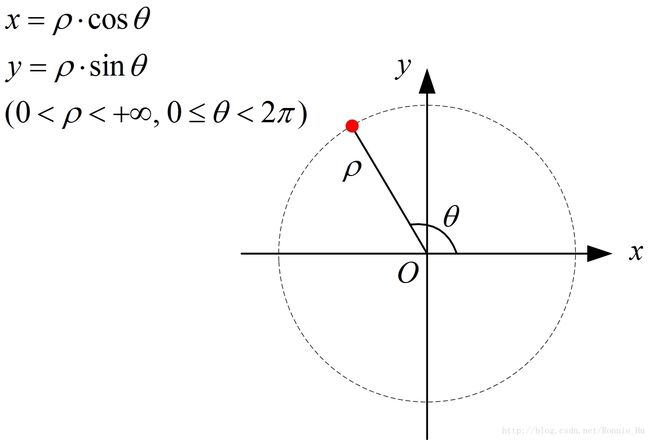
后来在从事电机控制工作时,才发现有个atan2函数,以前只知道有atan(反正切)函数。atan2函数,即所谓的四象限反正切函数,其本质就是运用极坐标来实现对角度的计算,相比于atan函数的取值范围(-pi/2, pi/2),atan2函数的取值范围为(-pi, pi],该函数之所以称之为四象限反正切函数,我想应该就是因为它能够区分四个象限,而atan函数是无法区分象限的。

Matlab中就有atan2函数,举例如下:
atan2(0,1) = 0
atan2(sqrt(3),1) = 1.0472,即pi/3
atan2(1,0) = 1.5708,即pi/2
atan2(-1,1) = -0.7854,即-pi/4
atan2(0,-1) = 3.1416,即pi
atan2(-0.001,-1) = -3.1406,接近-pi
TI的IQ_math中也有两个函数_IQatan2和_IQatan2PU,通过仿真,有如下结果,不难发现_IQatan2函数的取值范围为(-pi, pi],而_IQatan2PU函数的取值范围为[0, 1)。

