(李航统计学习方法)SVM的python实现
支持向量机是一种二分类模型,基本模型是定义在特征空间的间隔最大的线性分类器。间隔最大化使它有别于感知机。在面试中,经常遇到手推SVM,所以公式的推导也很重要。
模型:
策略:间隔最大化,形式化为求解凸二次规划,等价于正则化的合页损失函数最小化
算法:略
支持向量机包括:线性可分支持向量机,线性支持向量机,非线性支持向量机
间隔最大化的直观解释:对训练数据集找到几何间隔最大的超平面意味着以充分大的确信度对训练数据进行分类。使其面对最难分的实例点也有足够大的确信度将它们分开,这样在面对未知的新实例也有很好的分类预测能力。
支持向量:在数据线性可分的情况下,训练数据的样本点与分离超平面最近的样本点
献上我看到的最好的讲解:https://blog.csdn.net/v_july_v/article/details/7624837(因为链接中的大神讲解非常好,就不写自己的理解了)
关于smo的公式推导:https://www.jianshu.com/p/eef51f939ace
合页损失函数
支持向量机的另外一种解释就是最小化合页损失函数
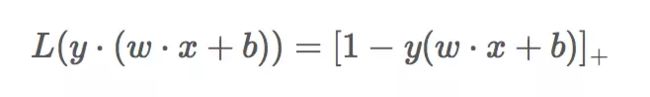
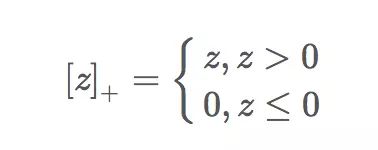
SVM的损失函数就是合页损失函数加上正则项,第一项是经验损失,第二项是w的L2范数;它与SVM求最优解的目标函数的形式很相似
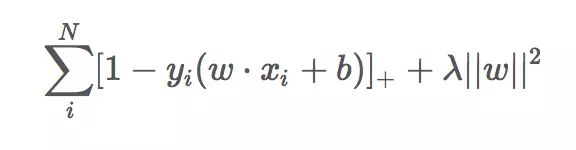
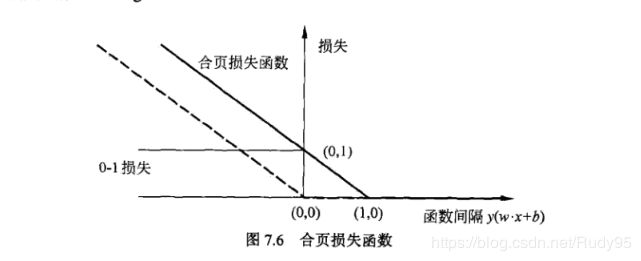
从图中我们可以看到,
1)0-1损失
当样本被正确分类时,损失为0;当样本被错误分类时,损失为1。
2)感知机损失函数
当样本被正确分类时,损失为0;当样本被错误分类时,损失为-y(wx+b)。
3)合页损失函数
当样本被正确分类且函数间隔大于1时,合页损失才是0,否则损失是1-y(wx+b)。
相比之下,合页损失函数不仅要正确分类,而且确信度足够高时损失才是0。也就是说,合页损失函数对学习有更高的要求。
python代码实现:
import numpy as np
from sklearn.metrics.pairwise import rbf_kernel
from scipy.io import loadmat
from sklearn import datasets
"""
svm模型
"""
def linearKernel():
"""线性核函数
"""
def calc(X, A):
return X * A.T
return calc
def rbfKernel(delta):
"""rbf核函数
"""
gamma = 1.0 / (2 * delta**2)
def calc(X, A):
return np.mat(rbf_kernel(X, A, gamma=gamma))
return calc
def getSmo(X, y, C, tol, maxIter, kernel=linearKernel()):
"""SMO, X 训练样本,y标签集 C正规化参数 tol容忍值 maxIter最大迭代次数,K所用的核
Args:
X 训练样本
y 标签集
C 正规化参数
tol 容忍值
maxIter 最大迭代次数
K 所用核函数
Returns:
trainSimple 简化版训练算法
train 完整版训练算法
predict 预测函数
"""
m, n = X.shape
# 存放核函数的转化结果
K = kernel(X, X)
# Cache存放预测误差,用以加快计算速度
ECache = np.zeros((m,2))
def predict(X, alphas, b, supportVectorsIndex, supportVectors):
"""计算权值向量
Args:
X 预测矩阵
alphas alphas
b b
supportVectorsIndex 支持向量坐标集
supportVectors 支持向量
Returns:
predicts 预测结果
这里因为对预测起作用的是支持向量,
非支持向量的前面的alphas为0,支持向量的0 1:
for k in validCaches:
if k==i: continue
Ek = E(k, alphas, b)
dist = np.abs(abs(Ei-Ek))
if maxDist < dist:
Ej = Ek
maxJ = k
maxDist = dist
return maxJ, Ej
else:
### 随机选择
j = selectJRand(i)
Ej = E(j, alphas, b)
return j, Ej
def select(i, alphas, b):
"""alpha对选择,对alphas的选择,优化alphas的值
"""
Ei = E(i, alphas, b)
# 选择违背KKT条件的,作为alpha2
####yi*f(xi)<-.001 alphas0.01 alphas>0,也就是alpha在0-C下,样本点不满足KKT的条件
Ri = y[i] * Ei
if (Ri < -tol and alphas[i] < C) or \
(Ri > tol and alphas[i] > 0):
# 选择第二个参数
j = selectJRand(i)
Ej = E(j, alphas, b)
# j, Ej = selectJ(i, Ei, alphas, b)
# get bounds
# ##alphas的边界,0= 0:
return 0, alphas, b
iOld = alphas[i].copy()
jOld = alphas[j].copy()
alphas[j] = jOld - y[j] * (Ei - Ej) / eta
if alphas[j] > H:
alphas[j] = H
elif alphas[j] < L:
alphas[j] = L
if abs(alphas[j] - jOld) < tol:
alphas[j] = jOld
return 0, alphas, b
alphas[i] = iOld + y[i] * y[j] * (jOld - alphas[j])
# update ECache,update Ecache,存放更新alpha后对应的样本的误差
updateE(i, alphas, b)
updateE(j, alphas, b)
# update b
bINew = b - Ei - y[i] * (alphas[i] - iOld) * Kii - y[j] * \
(alphas[j] - jOld) * Kij
bJNew = b - Ej - y[i] * (alphas[i] - iOld) * Kij - y[j] * \
(alphas[j] - jOld) * Kjj
if alphas[i] > 0 and alphas[i] < C:
bNew = bINew
elif alphas[j] > 0 and alphas[j] < C:
bNew = bJNew
else:
bNew = (bINew + bJNew) / 2
return 1, alphas, b
else:
return 0, alphas, b
def train():
"""完整版训练算法
Returns:
alphas alphas
w w
b b
supportVectorsIndex 支持向量的坐标集
supportVectors 支持向量
iterCount 迭代次数
"""
numChanged = 0
examineAll = True
iterCount = 0
alphas = np.mat(np.zeros((m, 1)))
b = 0
# 如果所有alpha都遵从 KKT 条件,则在整个训练集上迭代
# 否则在处于边界内 (0, C) 的 alpha 中迭代
while (numChanged > 0 or examineAll) and (iterCount < maxIter):
numChanged = 0
if examineAll:
for i in range(m):
changed, alphas, b = select(i, alphas, b)
numChanged += changed
else:
nonBoundIds = np.nonzero((alphas.A > 0) * (alphas.A < C))[0]
for i in nonBoundIds:
changed, alphas, b = select(i, alphas, b)
numChanged += changed
iterCount += 1
if examineAll:
examineAll = False
elif numChanged == 0:
examineAll = True
supportVectorsIndex = np.nonzero(alphas.A > 0)[0]
supportVectors = np.mat(X[supportVectorsIndex])
return alphas, w(alphas, b, supportVectorsIndex, supportVectors), b, \
supportVectorsIndex, supportVectors, iterCount
def trainSimple():
"""简化版训练算法
Returns:
alphas alphas
w w
b b
supportVectorsIndex 支持向量的坐标集
supportVectors 支持向量
iterCount 迭代次数
"""
numChanged = 0
iterCount = 0
alphas = np.mat(np.zeros((m, 1)))
b = 0
L = 0
H = 0
while iterCount < maxIter:
numChanged = 0
for i in range(m):
Ei = E(i, alphas, b)
Ri = y[i] * Ei
# 选择违背KKT条件的,作为alpha2
if (Ri < -tol and alphas[i] < C) or \
(Ri > tol and alphas[i] > 0):
# 选择第二个参数
j = selectJRand(i)
Ej = E(j, alphas, b)
# get bounds
if y[i] != y[j]:
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
if L == H:
continue
Kii = K[i, i]
Kjj = K[j, j]
Kij = K[i, j]
eta = 2.0 * Kij - Kii - Kjj
if eta >= 0:
continue
iOld = alphas[i].copy();
jOld = alphas[j].copy()
alphas[j] = jOld - y[j] * (Ei - Ej) / eta
if alphas[j] > H:
alphas[j] = H
elif alphas[j] < L:
alphas[j] = L
if abs(alphas[j] - jOld) < tol:
alphas[j] = jOld
continue
alphas[i] = iOld + y[i] * y[j] * (jOld - alphas[j])
# update b
bINew = b - Ei - y[i] * (alphas[i] - iOld) * Kii - y[j] * \
(alphas[j] - jOld) * Kij
bJNew = b - Ej - y[i] * (alphas[i] - iOld) * Kij - y[j] * \
(alphas[j] - jOld) * Kjj
if alphas[i] > 0 and alphas[i] < C:
b = bINew
elif alphas[j] > 0 and alphas[j] < C:
b = bJNew
else:
b = (bINew + bJNew) / 2.0
numChanged += 1
if numChanged == 0:
iterCount += 1
else:
iterCount = 0
supportVectorsIndex = np.nonzero(alphas.A > 0)[0]
supportVectors = np.mat(X[supportVectorsIndex])
return alphas, w(alphas, b, supportVectorsIndex, supportVectors), b, \
supportVectorsIndex, supportVectors, iterCount
return trainSimple, train, predict
if __name__ == '__main__':
data = loadmat('data/ex6data1.mat')
X = np.mat(data['X'])
y = np.mat(data['y'], dtype=np.float)
y[y == 0] = -1
m, n = X.shape
tol = 1e-3
maxIter = 20
# C = 1.0
C = 100.0
trainSimple, train, predict = getSmo(X, y, C, tol, maxIter)
alphas, w, b, supportVectorsIndex, supportVectors, iterCount = train()
print(w)
print(b)
print(len(supportVectorsIndex))
print('iterCount:%d' % iterCount)
predictions = predict(X, alphas, b, supportVectorsIndex, supportVectors)
errorCount = (np.multiply(predictions, y).A < 0).sum()
print('error rate: %.2f' % (float(errorCount) / m))
代码的流程:
初始化,所有的alpha都为0,b为0
第一轮遍历:
1、遍历整个数据集,计算每个样本在初始条件下是否满足KKT条件(y_i*f(x_i)>=1)
满足:则跳过
不满足:则作为第一个alpha_1,再遍历数据集找到|E2-E1|最大的对应的alpha作为alpha_2
2、根据alpha的公式更新alpha_2
3、判断更新后的alpha_2是否在约束条件内,不在则取边缘条件的取值;判断更新的alpha_2与alpha_2_old差值
超过容忍度:计算alpha_1的值,更新b的取值
如果小于容忍度:alpha_2仍然取旧的值
4、当更新后的alpha_1和alpha_2都满足KKT的约束条件,b取更新后的值;否,则取alpha_1和alpha_2各自对应更新的值的均值
第二轮遍历:
对alphas中满足0
5、根据alphas中大于0的作为支持向量
6、依据更新完毕的alphas和支持向量做predict
补充:通过分类决策函数可以发现,与感知机是一样的
整个公式推导的流程:
间隔最大化(函数间隔,几何间隔)——优化目标函数——使用对偶问题求解(要满足KKT条件对偶问题的最优解才是原问题的最优解)——使用SMO序列最小最优算法求解
(整个公式的推导过程应该时刻注意约束条件)
公式推导手撕版(没有考虑核函数):



核函数的介绍以及选择:

主要是针对线性核,多项式核,和高斯核进行讨论:
一般推荐在做训练之前对数据进行归一化,当然测试集中的数据也需要归一化。。
2)在特征数非常多的情况下,或者样本数远小于特征数的时候,使用线性核,效果已经很好,并且只需要选择惩罚系数C即可。
3)在选择核函数时,如果线性拟合不好,一般推荐使用默认的高斯核’rbf’。这时我们主要需要对惩罚系数C和核函数参数γ进行艰苦的调参,通过多轮的交叉验证选择合适的惩罚系数C和核函数参数γ。
4)理论上高斯核不会比线性核差,但是这个理论却建立在要花费更多的时间来调参上。所以实际上能用线性核解决问题我们尽量使用线性核。
针对高斯核的两个参数C和 γ \gamma γ:
C是控制软间隔的松弛系数的大小,可以看作是正则项,当C比较大时,我们的损失函数也会越大,这意味着我们不愿意放弃比较远的离群点。这样我们会有更加多的支持向量,也就是说支持向量和超平面的模型也会变得越复杂,也容易过拟合。反之,当C比较小时,意味我们不想理那些离群点,会选择较少的样本来做支持向量,最终的支持向量和超平面的模型也会简单。scikit-learn中默认值是1。
γ \gamma γ主要定义了单个样本对整个分类超平面的影响,当γ比较小时,单个样本对整个分类超平面的影响比较小,不容易被选择为支持向量,反之,当 γ \gamma γ比较大时,单个样本对整个分类超平面的影响比较大,更容易被选择为支持向量,或者说整个模型的支持向量也会多。scikit-learn中默认值是 1 / 样 本 特 征 数 1/样本特征数 1/样本特征数
对C和 γ \gamma γ的调参:
使用网格搜索,使用交叉验证,寻找出最佳的参数。