【python学习笔记】13：用梯度下降法求解最优值问题

梯度是函数在某点沿每个坐标的偏导数构成的向量，它反映了函数沿着哪个方向增加得最快。因此要求解一个二元函数的极小值，只要沿着梯度的反方向走，直到函数值的变化满足精度即可。

这里打表存储了途径的每个点，最后在图上绘制出来以反映路径。

*梯度下降的具体实现

 

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

def Fun(x,y):#原函数
    return x-y+2*x*x+2*x*y+y*y

def PxFun(x,y):#偏x导
    return 1+4*x+2*y

def PyFun(x,y):#偏y导
    return -1+2*x+2*y

#初始化
fig=plt.figure()#figure对象
ax=Axes3D(fig)#Axes3D对象
X,Y=np.mgrid[-2:2:40j,-2:2:40j]#取样并作满射联合
Z=Fun(X,Y)#取样点Z坐标打表
ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap="rainbow")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')

#梯度下降
step=0.0008#下降系数
x=0
y=0#初始选取一个点
tag_x=[x]
tag_y=[y]
tag_z=[Fun(x,y)]#三个坐标分别打入表中，该表用于绘制点
new_x=x
new_y=y
Over=False
while Over==False:
    new_x-=step*PxFun(x,y)
    new_y-=step*PyFun(x,y)#分别作梯度下降
    if Fun(x,y)-Fun(new_x,new_y)<7e-9:#精度
        Over=True
    x=new_x
    y=new_y#更新旧点
    tag_x.append(x)
    tag_y.append(y)
    tag_z.append(Fun(x,y))#新点三个坐标打入表中

#绘制点/输出坐标
ax.plot(tag_x,tag_y,tag_z,'r.')
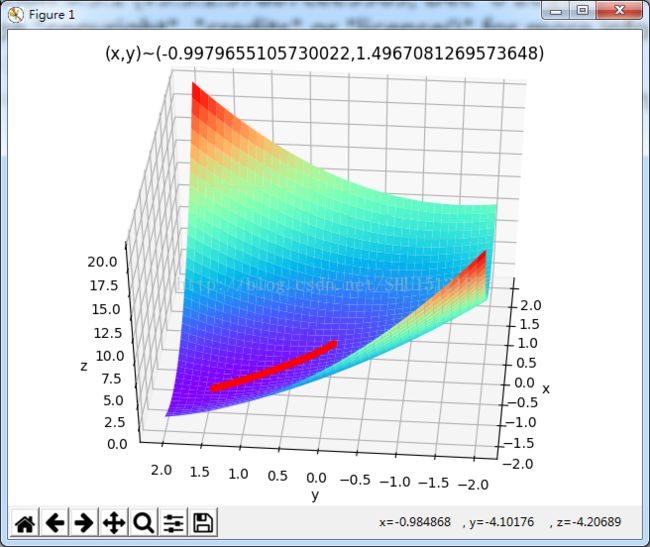
plt.title('(x,y)~('+str(x)+","+str(y)+')')
plt.show()

运行结果：

 

 

换个角度看：

 

验证结果是否正确：