吃饭【网络流】

题目大意：

有 n n 头牛，每头牛有自己喜欢的食物和饮料，每种食物或饮料只有一个。求最多能让多少头牛吃到食物并喝到饮料。
Input I n p u t

4 3 3
2 2 1 2 3 1
2 2 2 3 1 2
2 2 1 3 1 2
2 1 1 3 3

Output O u t p u t

3

---

思路：

很明显的最大流题目。这道题匈牙利会超时，正解是 Dinic D i n i c 。
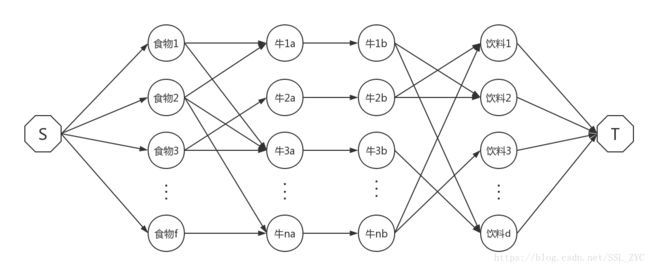
这道题最难的也就是考点是建图。很容易想到这样的建法（权值均为1）：

但是这样的话，就有可能一头牛吃多个食物及饮料，例如上图中牛 1 1 可以既吃食物 1 1 ，饮料 2 2 组成的套餐，又可以吃食物 2 2 ，饮料 d d 组成的套餐。
所以，这里就要拆点。将一头牛拆成两头，中间连一条权值为 1 1 的线，就可以保证不会有一头牛吃多组套餐的情况。

---

代码：

#include 
#include 
#include 
#include 
#define Inf 0x7f
#define INF 2147483647
using namespace std;

int n,f,d,s,t,ans,sum,num,fnum,dnum,x,k,head[5000001],dep[5000001];

struct edge
{
    int c,to,next;
}e[5000001];

void add(int from,int to,int c)
{
    k++;
    e[k].to=to;
    e[k].c=c;
    e[k].next=head[from];
    head[from]=k;
}

bool bfs()  //分层
{
    memset(dep,Inf,sizeof(dep));
    queue<int> q;
    q.push(s);
    dep[s]=0;
    while (q.size())
    {
        int u=q.front();
        q.pop();
        for (int i=head[u];i;i=e[i].next)
        {
            int v=e[i].to;
            if (dep[v]>dep[u]+1&&e[i].c)
            {
                dep[v]=dep[u]+1;
                q.push(v);
            }
        }
    }
    return (dep[t]int dfs(int u,int low)
{
    int lows=0;
    if (u==t) return low;
    for (int i=head[u];i;i=e[i].next)
    {
        int v=e[i].to;
        if (dep[v]==dep[u]+1&&e[i].c) 
        {
            lows=dfs(v,min(low,e[i].c));  //继续找增广路
            if (!lows) continue;
            e[i].c-=lows;  //正向边
            e[(i+1)^1-1].c+=lows;  //反向边
            return lows;
        }
    }
    return 0;
}

int main()
{
    //建图时牛a编号为1~n，牛b编号为n+1~2n，食物编号为2n+1~2n+f，饮料编号为2n+f+1~2n+f+d
    scanf("%d%d%d",&n,&f,&d);
    s=0;
    t=n+n+f+d+1;
    for (int i=1;i<=n;i++)
    {
        scanf("%d%d",&fnum,&dnum);
        for (int j=1;j<=fnum;j++)  //食物连向牛a
        {
            scanf("%d",&x);
            add(n+n+x,i,1);
            add(i,n+n+x,0);
        }
        for (int j=1;j<=dnum;j++)  //牛b连向饮料
        {
            scanf("%d",&x);
            add(n+i,n+n+f+x,1);
            add(n+n+f+x,n+i,0);
        }
    }
    for (int i=1;i<=n;i++)  //牛a连向牛b
    {
        add(i,n+i,1);
        add(n+i,i,0);
    }
    for (int i=1;i<=f;i++)  //S连向食物
    {
        add(s,n+n+i,1);
        add(n+n+i,s,0);
    }
    for (int i=1;i<=d;i++)  //饮料连向T
    {
        add(n+n+f+i,t,1);
        add(t,n+n+f+i,0);
    }
    while (bfs())
    {
        while (sum=dfs(s,INF))
         ans+=sum;  
    }
    printf("%d\n",ans);
    return 0;
}