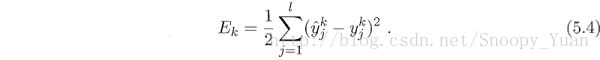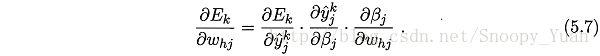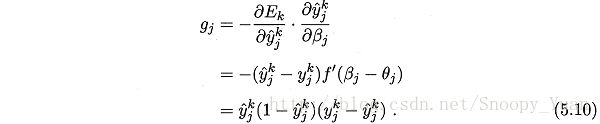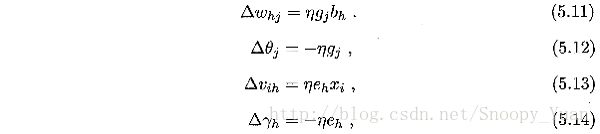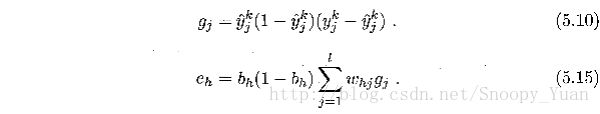神经网络基础 - Python编程实现标准BP算法

编程基于python，完整代码托管在我的Github PY131/Practice-of-Machine-Learning，欢迎访问。

基础知识参考“周志华《机器学习》第五章-神经网络”

1. BP算法分析

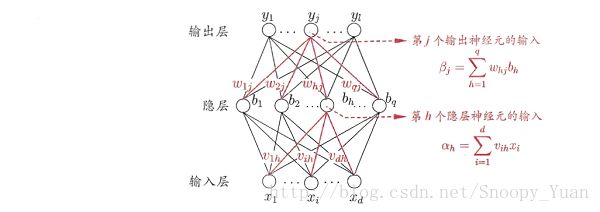
如下图所示BP网络：

对样本 a = (x_k,y_k)，其输出为 ^y_k，即是：

由此得出在样本 a 上的均方误差：

我们的目标是是所有样本得出的均方误差最小化，为此我们要找到最优的参数（即上图中的连接权(w, v)及对应阈值(θ, γ)）。考虑梯度下降法。比如对于 w = w+Δw，梯度下降法调整式为：

式中，η 是学习率，他控制着算法迭代步长，直接关系着算法的收敛速度甚至收敛性。

对于图示BP网络，梯度项有：

其中：

当采用Sigmoid函数作为每个神经元的激活函数是，可以根据其导数性质：

来得出最终的梯度项 g_j*b_h，其中：

于是得出BP算法关于参数 w 的更新公式：

同样的方式可以推导出其他参数的更新公式，综上，可以得出BP算法中参数的更新公式如下：

其中：

经过上面的推导，给出标准BP算法如下图所示：

Algorithm 1. 标准BP算法
----
    输入： 训练集 D，学习率 η.
    过程： 
        1. 随即初始化连接权与阈值 (ω，θ).
        2. Repeat：
        3.   for x_k，y_k in D:
        4.     根据当前参数计算出样本误差 E_k.
        5.     根据公式计算出随机梯度项 g_k.
        6.     根据公式更新 (ω，θ).
        7.   end for
        8. until 达到停止条件
    输出：(ω，θ) - 即相应的多层前馈神经网络.
----

2. BP算法编程实现

采用python编程实现上面的算法，首先明确一些需求：

• 程序应保留神经网络结构调整的灵活性，主要面向隐层节点数的变动；
• 程序应保留激活函数重载功能，此处先采用Sigmoid激活函数；
• 程序应保留学习率设置功能，此处先采用固定学习率实现；
• 程序应具有快速高效，如考虑python-numpy进行高效的矩阵运算；
• …

下面是简单的标准BP算法程序示例：

def BackPropagate(self, x, y, lr):
    '''
    the implementation of BP algorithms on one slide of sample

    @param x, y: array, input and output of the data sample
    @param lr: float, the learning rate of gradient decent iteration
    '''

    # dependent packages
    import numpy as np 

    # get current network output
    self.Pred(x)

    # calculate the gradient based on output
    o_grid = np.zeros(self.o_n) 
    for j in range(self.o_n):
        o_grid[j] = (y[j] - self.o_v[j]) * self.afd(self.o_v[j])

    h_grid = np.zeros(self.h_n)
    for h in range(self.h_n):
        for j in range(self.o_n):
            h_grid[h] += self.ho_w[h][j] * o_grid[j]
        h_grid[h] = h_grid[h] * self.afd(self.h_v[h])   

    # updating the parameter
    for h in range(self.h_n):  
        for j in range(self.o_n): 
            self.ho_w[h][j] += lr * o_grid[j] * self.h_v[h]

    for i in range(self.i_n):  
        for h in range(self.h_n): 
            self.ih_w[i][h] += lr * h_grid[h] * self.i_v[i]     

    for j in range(self.o_n):
        self.o_t[j] -= lr * o_grid[j]    

    for h in range(self.h_n):
        self.h_t[h] -= lr * h_grid[h]

完整的程序实现点击查看

3. 分类实验

完整实验程序

这里我们采用sklearn自带的数据集生成器Samples generator中的make_circles和make_moons()函数来生成两个二分类的非线性可分数据集：

数据集生成程序示例（生成circles数据）：

# 生成circle数据集，并添加一定的噪声  
from sklearn.datasets import make_circles 
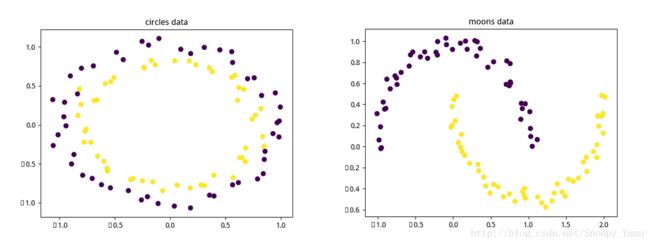
X, y = make_circles(100, noise=0.10)  # 2 input 1 output

数据点如下图所示：

从图中可以看出，数据是二分类非线性可分的。采用神经网络对其分类模式进行学习是个不错的选择。

生成BP网络并初始化，这里通过编程实现的一个BP网络类，各种操作及相关变量在类中定义。

下面是搭建网络并训练的示例程序：

nn = BP_network()  # build a BP network class
nn.CreateNN(2, 6, 1, 'Sigmoid')  # build the network # 隐层节点数为6

for i in range(500): # 迭代500次
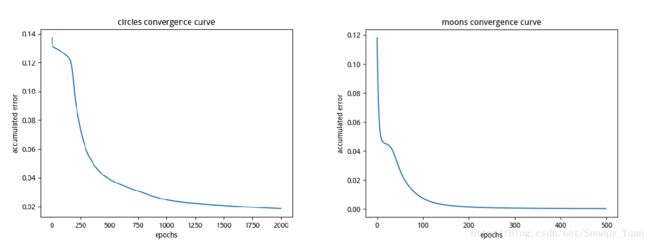
    err, err_k = nn.TrainStandard(X, y.reshape(len(y),1), lr=0.5)

经过大量的迭代训练，可以观察出神经网络在训练样本上的误差收敛情况，如下图示（由于circles的分类较困难一些，故而其上的迭代进行的次数多一些）：

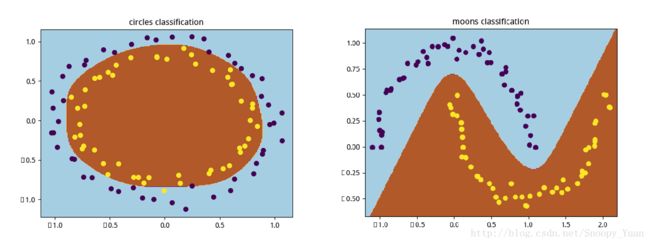
最总得出的分类决策区域绘制如下图：

可以看出，神经网络的分类决策区域还是比较精确的，进一步，为考虑所训练的模型的泛化性能，可将数据集拆分为训练集与测试集进行重新训练与测试，并可以采用交叉验证法等方法。

4. 小结

这里基于python编程实现了标准BP算法，并采用两种有趣的数据集来进行的实验。这里给出实验中的一些总结：

• BP神经网络训练往往需要大量的计算（体现在迭代次数多，矩阵运算规模大等）；
• 标准BP算法对参数较为敏感，如学习率，迭代次数，隐层节点数等都需要注意；
• 一般来说，足够多隐层节点的BP网络能够逼近任意目标函数，但训练数据集的不充分性始终存在，要特别注意过拟合问题。