【牛客网】算法学习笔记

$1.时间复杂度$

     1.1 常数时间的操作：一个操作如果和数据量没有关系，每次都是
固定时间内完成的操作，叫做常数操作。

    1.2 时间复杂度为一个算法流程中，常数操作数量的指标。常用O
（读作big O）来表示。具体来说，在常数操作数量的表达式中，
$只要高阶项，不要低阶项，也不要高阶项的系数$,剩下的部分
如果记为f(N)，那么时间复杂度为O(f(N))。

    1.3 评价一个算法流程的好坏，先看时间复杂度的指标，然后再分
析不同数据样本下的实际运行时间，也就是常数项时间。

$2.对数器的概念和使用$

对数器可以验证你的算法正确性

对数器的构造和使用如下步骤：
0，有一个你想要测的方法a，
1，实现一个绝对正确但是复杂度不好的方法b（思路简单好实现的方法），
2，实现一个随机样本产生器
4，实现比对的方法
4，把方法a和方法b比对很多次来验证方法a是否正确。
5，如果有一个样本使得比对出错，打印样本分析是哪个方法出
错
6，当样本数量很多时比对测试依然正确，可以确定方法a已经
正确

也就是说：有一个绝对正确的方法，和你的算法的，在同一情况下，数据样本量相同，但是，是两组“不同”数据，即内存中占有不同的位置，用对数器和你的算法，将结果进行比较（第4步实现），当结果完全相同，并且在样本数量很多的情况下。就可以确定你的算法的正确性。对数器在史记应用中很重要

$3.递归行为及其实质剖析$

    3.1 简单来讲就是自己调用自己，这是上课时老师的讲法。。但却没有讲清楚到底是怎么调用。

    3.2递归呢，其实就是大问题化为小问题。这儿含有分治的思想。
就比如，你要求一个数组中的最大值，分为两半，分别求最大值，合起来再求最大值

    3.3 $递归函数其实就是系统在帮助你压栈，执行流程如下:$
         3.3.1 进入求解最大值函数
        3.3.2 程序由上至下执行，到子过程这一行时，即开始发生递归行为时。开始压栈，栈里面会记录这个函数执行到哪一行，及其所有参数和这个函数的所有信息。然后就调用子过程
        3.3.4 调用子过程时，也会遇到子过程的子过程。这时，如法炮制，将记录子过程的所有信息。跑去执行子过程的子过程，直到跳出此循环。
        3.3.5 当调出循环以后，将栈顶的信息弹出。子过程就会接受这个信息（之前就是它压进栈的），继续跑下去。按照程序的执行顺序，就可以如此这般的跑完。

$一句话，任何递归行为都可以改为非递归行为，即迭代$
递归行为求时间复杂度：master公式的使用

使用范围：子过程的规模一样(差一个两个的数据是不影响规模的)
$$T(N)=a\ast T(N/b)+O(N^d)$$
$1)log(b,a)>d时，复杂度为O(N^{log(b,a)})$
$2)log(b,a)=d时，复杂度为O(N^d\ast logN)$
$3)log(b,a)<d时，复杂度为O(N^d)$

补充阅读master

$4.排序$

排序算法动图演示

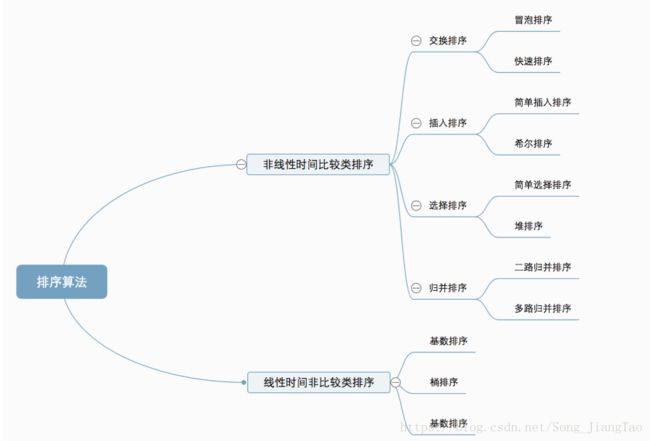
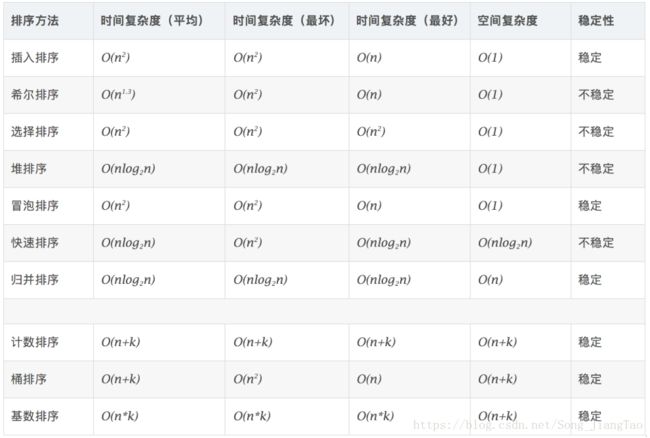
图中的稳定性，不是说复杂度的时高时低。其实就是概率的问题。长期期望情况。

稳定性的意义： 在一次排序完成以后，下一次根据其他条件排序的情况下，能否实现相等位置的稳定。在实际应用中有这种需求。

例如：有1班，2班，3班这3个班的人的成绩由高到低排序，当再一次根据班级排序时，班内的成绩也是由高到低。这样就具有稳定性。
4.1 冒泡排序
4.2 选择排序
4.3 插入排序
4.4 归并排序
4.5 快速排序

     4.5.1 荷兰国旗问题:
给定一个数组arr，和一个数num，请把小于num的数放在数组的
左边，等于num的数放在数组的中间，大于num的数放在数组的
右边。
    4.5.2 经典快排:
选取待排序列的一个数（可取最后一个数），小于等于它的放左边，大于它的放右边。相等的数不动。左右两边继续执行此过程。也就是说，每一次至少能确定一个数
    4.5.3 随机快排:
随机选一个数，和最后一个数交换，做快排。这样做，是一个概率问题。长期期望的情况下其时间复杂度$O(N\ast logN)$，这个在实际应用中大量使用。空间复杂度的长期期望为$O(logN)$
4.6 $堆排序$
4.6.1 堆

堆实际上就是完全二叉树，在计算机中，堆也是数组形式。堆只是抽象出来的一个概念。任何一个结点的左孩子：$2\ast i+1，i是该结点的下标$，右孩子$2\ast i+2$，父节点$(i-1)/2$。

4.6.1.1 大根堆

任何子树的根结点的关键字都是最大值。

建立大根堆根结点和两个孩子中较大的一个比较，较大的换上去。孩子继续执行此过程。还可以从叶子结点往上比较。

    4.6.1.2 小根堆
任何子树的根结点的关键字都是最小值。
    4.6.2 堆排序的过程
先让一个数组变化为大根堆。然后最后一个数和堆的根结点交换，此时最大值到达数组的最后一位，此时不在变换最后一个数。在重新调整为大根堆，最后的数在和大根堆的根结点交换。如此这般，就实现了排序

    4.6.3 堆排序的细节和复杂度分析
时间复杂度O(N*logN)，额外空间复杂度O(1)
堆结构非常重要
1，堆结构的heapInsert与heapify
2，堆结构的增大和减少
3，如果只是建立堆的过程，时间复杂度为O(N)
4，优先级队列结构，就是堆结构

4.7 工程中的综合排序算法
工程中，

如果数组长度较长，会先对数组中的元素类型进行判断，到底是基础型（int…），还是自定义的类型。如果是前者，则会使用快排。因为基础型的数据相同值没有差别。如果是自己定义的类类型，根据字段排序，则会使用归并。因为自定义的数据相同可能会有不同的意义

如果数组长度很短（小于60），则直接插入排序，因为插排的常数项很低。所以速度会很快

4.8 有关排序问题的补充：
1，归并排序的额外空间复杂度可以变成O(1)，但是非常难，不
需要掌握，可以搜“归并排序 内部缓存法”
2，快速排序可以做到稳定性问题，但是非常难，不需要掌握，
可以搜“01 stable sort”
3，有一道题目，是奇数放在数组左边，偶数放在数组右边，还
要求原始的相对次序不变，碰到这个问题，可以怼面试官。面试
官非良人。

#下面介绍一些题目，需要源码请留言邮箱。
4.9 桶排序、计数排序、基数排序的介绍
1，非基于比较的排序，与被排序的样本的实际数据状况很有关系，所
以实际中并不经常使用
2，时间复杂度O(N)，额外空间复杂度O(N)
3，稳定的排序

补充：给定一个数组，求如果排序之后，相邻两数的最大差值，要求时间复杂度O(N)，且要求不能用非基于比较的排序。

解决思路： 数组中N个数，设计N+1个桶，第一个桶放这个数组的最小值，最后一个桶放最大值，然后，中间的桶放置其他数，这其中必定有一个空桶，这样就可以排除，最大差值一定不在同一桶内！所以，结果必定在不同的桶内。
然后，每个桶记录这个桶的最大值和最小值，以及是否为空桶这3条信息。然后，比较每一个非空桶的最小值和左边距离最近的非空桶的最大值的差值。我们要的答案就在这些值当中！

4.10 用栈实现队列的功能
使用两个栈，分别叫栈1，栈2，然后在栈1中依次存放12345，这5个数据，要实现队列的功能（先进先出）只需要把，栈1的信息依次存到栈2里，即54321，这样即可满足队列的功能，这样做有两个条件栈2必须是空的。栈1要存就全部存

4.11 用队列实现栈的功能
用两个队列，分别叫队列1，队列2，在队列1中存放12345，这5个数据，诗选栈的功能（先进后出），只需把，队列1的1234存到队列2中，那么队列1中就取到了应该取的数，同理要取4，只要把队列2的123存放到队列1即可实现。

4.12 用数组结构实现大小固定的队列和栈
我们就固定大小为3
队列：一个队列，存放123，这3个数据，用两个指针，分别叫end，start，均指向1，取数据，end向后移动，即指向2，继续取，end指向3，存数据，存到start指向的位置，即1位置，存放完毕以后，start向后移动，指向2，继续取，发现到底了，重新返回1位置。如此这般。

栈：一个栈，用一个指针index，指向栈底。这个指针的含义就是表示新进来的数存放的位置。

数据2的抹掉与否并步影响结果，因为新来一个数就会把2盖过去。

4.13 转圈打印矩阵
【要求】 额外空间复杂度为O(1)。
$$\left(\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right)$$
打印为 123 69 87 45。
解决思路：二维数组，给定(0,0)点和(2,2)点，两个点可以决定这个矩阵的最外圈部分，依次类推。

4.14旋转正方形矩阵
【要求】 额外空间复杂度为O(1)。
$$\left(\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right)$$
旋转为
$$\left(\begin{array}{ccc}7& 4& 1\\ 8& 5& 2\\ 9& 6& 3\end{array}\right)$$
**解决思路：**给定左上角点和右下角点。其实就是，在原来的矩阵中1和3，和5连线构成90°角。所以他俩交换位置。同理，2和6，6和8，8和4，4和2。依次交换即可。
4.15之字形打印矩阵
【题目】 给定一个矩阵matrix，按照“之”字形的方式打印这个矩阵，例如： 1 2 3， 4 5 6， 7 8 9 “之”字形打印的结果为：1，2，4，7，5，3，6，8，9。
【要求】 额外空间复杂度为O(1)。
$$\left(\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right)$$
解决思路： a，b均指向（0，0）点，a由左向右变，直到结尾向下。b由上向下变，直到结尾向右。每次的移动互不干扰，结果他俩每次都能练成一条对角线。所以，我们要做的就是设计出打印对角线的方法，不过是从右上到左下，还是左下到右上的问题。

就算不是n*n的矩阵，道理是一样的

$总之，这种打印问题，当局部变化的规律很难发现，或者没有的时候，我们只能将思维跳出来，宏观的看待这个问题$

4.16在行列都排好序的矩阵中找数
【题目】 给定一个有N*M的整型矩阵matrix和一个整数K，matrix的每一行和每一 列都是排好序的。实现一个函数，判断K是否在matrix中。
【要求】 时间复杂度为O(N+M)，额外空间复杂度为O(1)。
$$\left(\begin{array}{cccc}1& 2& 3& 4\\ 5& 6& 7& 8\\ 9& 10& 11& 12\end{array}\right)$$
**解决思路：**假设我们要找5，我们从右上角或者左下角开始找起。
从右上角找：
第一步：4<5，所以4的左边都排除（因为都排好序了），往下走来到8的位置
第二步：8>5，所以8的下边排除，往左走来到7的位置。
第三步：7>5，所以7的下边排除，往左走来到6的位置。
。。。直到找到或者越界为止。
总之一句话，小于它往下走，大于它往左走
从左下角找是一个道理
$这种优秀的解的来源：一，从它的数据状况（排好序之类的）出发开始想解$
$二，从它的问法，开始想解。。。这样做就可以把解优化$
4.17判断一个链表是否为回文结构
【题目】 给定一个链表的头节点head，请判断该链表是否为回文结构。
例如： 1->2->1，返回true。 1->2->2->1，返回true。15->6->15，返回true。 1->2->3，返回false。

进阶： 如果链表长度为N，时间复杂度达到O(N)，额外空间复杂
度达到O(1)。

**解决思路：**最简单的方法：把链表存到栈里面，弹出栈和原链表比较。
空间复杂度为O(1)的情况：准备一个快指针（一次跳2步），一个慢指针（一次跳一步），链表大小为奇数情况下：当快指针跳到结尾时，慢指针指向中间值，这时把链表后半部分的数，反指向。（在12321的例子中，就是2的next指向3，1的next指向2），然后在和前半部分比较。

4.18复制含有随机指针节点的链表
【题目】 一种特殊的链表节点类描述如下：
public class Node {
public int value; public Node next; public
Node rand;
public Node(int data) { this.value = data; }
}

Node类中的value是节点值，next指针和正常单链表中next指针的意义
一 样，都指向下一个节点，rand指针是Node类中新增的指针，这个指
针可 能指向链表中的任意一个节点，也可能指向null。 给定一个由
Node节点类型组成的无环单链表的头节点head，请实现一个 函数完成
这个链表中所有结构的复制，并返回复制的新链表的头节点。

进阶：不使用额外的数据结构，只用有限几个变量，且在时间复杂度为 O(N)
内完成原问题要实现的函数

4.19两个单链表相交的一系列问题
【题目】 在本题中，单链表可能有环，也可能无环。给定两个
单链表的头节点 head1和head2，这两个链表可能相交，也可能
不相交。请实现一个函数， 如果两个链表相交，请返回相交的
第一个节点；如果不相交，返回null 即可。 要求：如果链表1
的长度为N，链表2的长度为M，时间复杂度请达到 O(N+M)，额外
空间复杂度请达到O(1)。

4.20在二叉树中找到一个节点的后继节点
【题目】 现在有一种新的二叉树节点类型如下：
public class Node {
public int value; public Node left;
public Node right; public Node parent;
public Node(int data) { this.value = data; }
}
该结构比普通二叉树节点结构多了一个指向父节点的parent指针。假
设有一 棵Node类型的节点组成的二叉树，树中每个节点的parent指针
都正确地指向 自己的父节点，头节点的parent指向null。只给一个在
二叉树中的某个节点 node，请实现返回node的后继节点的函数。在二
叉树的中序遍历的序列中， node的下一个节点叫作node的后继节点。

**解决思路：**两点：一个结点如果右孩子，那么就找右孩子所构成的这颗子树里面的最左结点；如果没有右孩子，那么就往上找，直到找到它父结点的左孩子等于当前结点（当前node），此时父节点就是所给node的后继。

寻找前驱结点的过程，正好和寻找后继结点，镜像对称

4.21介绍二叉树的序列化和反序列化
序列化只需记着两点，先序中序后序本质上是一样的，比如说先序遍历：每个value用！分割，遇到空用#表示，当然空也是“value”，也需要！分割，重要的是要把所有的空记录下来，这样才能还原结构。

反序列化就是把序列化的字符串在画出来就行。因为你有“结构”。总之呢，就是你怎么序列化的就怎么反序列化

4.22判断一棵二叉树是否是平衡二叉树
$树形DP$百度这个词条了解。

4.23判断一棵树是否是搜索二叉树、判断一棵树是否是完全二叉树

解决思路：
搜索二叉树：中序遍历，value为升序即为搜索二叉树，那么在实现中序遍历二叉树的输出位置，替换为逻辑判断大小即可解决。

完全二叉树：两种情况：1：遍历时发现任意一个结点有右孩子没有左孩子，返回false
2：遍历时当发现第一个结点有左孩子没有右孩子，或者左右都没有时，剩下的结点必须是叶子结点。

$5.哈希函数$

5.1哈希的性质
    5.1.1 经典哈希函数的输入域无穷大
    5.1.2 输出域有穷。
    5.1.3 哈希函数没有随机值。★即输入一样，输出也一样★，
    5.1.4 因为输入域无穷大，输出域有穷，所以必定存在多个输入对应一个输出
    5.1.5 由于哈希函数的离散性，所有的输入总是“均匀的”分布在所有的输出中。例如：有0~98个输入，输出 0~2。在0位置有33个左右的输入，其他也相同。
        5.1.5.1 离散性的推论：当所有的输入对应的输出都模一个数m，那么在输出0~m-1上也是“均匀分布的”
$大数据题目：哈希函数可以用来分流。即把大问题化小问题$

5.2认识布隆过滤器
场景： 一份黑名单有100亿个URL，每个url假设是64字节。
    假设我们要用HashSet()来做，那么付出的止url的内存空间就是640G，其他的细节不提。这在工程上是很大的浪费。

所以我们考虑一种新的模式：
    使用布隆过滤器，首先布隆过滤器是某种类型的set集合，缺点是有失误率。（当面试官不满意你的前面的设计时，你可以问他一句，是否允许有小的失误率。允许的话**（一般都是套路。。。所以肯定允许，而且在大数据的样本下，失误率一般都很小，所以是可以容忍的）**可以使用布隆过滤器）

具体过程：准备一个m大小的比特类型的数组，将一个url经过k个哈希函数的处理，得到哈希码，哈希码在求模m，这样就可以把哈希码对应到数组中（抹黑该位置）。这样处理以后，每个url得到k个抹黑位置，以此类推，其他的url也都这样做。怎么找呢？我们这样认为，如果这个url对应的k个位置都在数组里，就认为这个url在黑名单里，有一个不是黑的，就不在黑名单里，这样处理以后有很大部分的位置都被抹黑，所以，就存在都被抹黑的情况，这样，失误率就升高。所以可以用数组的大小和k的大小，宏观的调整失误率
一个公式：

$$m=\frac{n\ast lnp}{(ln2{)}^2}$$其中n是样本量，p是失误率，ln是自然对数，m是数组大小，m的单位是比特，除以8以后是字节。1G=1024M=1024×1024K=1024×1024×1024byte=1024×1024×1024×8bit

$$k=ln2\ast \frac{m}{n}$$其中k是哈希函数的数量
$$(1-e^{-\frac{n\ast k}{m}}{)}^k$$这个公式计算的是真实的失误率