《机器学习实战》 Ch8回归 代码运行总结

1、window下python2.7与python3.5两版本共存设置

　　机器学习实战代码基于python2.*，就存在python2与python3共存问题，设置如下：

• 在Path环境变量中检查以下4个变量

c:\Python27
c:\Python27\Scripts
c:\Python35
c:\Python35\Scripts

• 进入Python2.7安装目录，把Python.exe重命名为python2.exe
• 进入python3.5安装目录，把python.exe重命名为python3.exe

• 最后打开命令行界面测试一下

  　　执行python2命令会进入python2.7的交互环境，执行python3命令会进入python3.3交互环境。

• pip的问题

  　　两个python版本分别安装了pip以后怎么区分它们。进入python安装路径找到Scripts文件夹，进入里面找到pip*-script.py，打开修改第一句为你要指定的那个python解释器。
  （不过我并没有找到这个文件，没有改现没有问题出现）

2、windows下python安装Numpy、matplotlib模块

针对python2.7：

• numpy下载: numpy-1.8.2-win32-superpack-python2.7；

• matplotlib下载:

  　　matplotlib是python中强大的画图模块，这里使用pip来安装，用源码安装据说会比较麻烦，进入到CMD窗口下，执行python -m pip install -U pip setuptools进行升级。
  
  　　接着键入python -m pip install matplotlib进行自动的安装，系统会自动下载安装包。正常情况下，pip会下载其它的关连安装包，并完成最终的安装，具体参考下图所示。
  
  　　安装完成后，可以用python -m pip list查看本机的安装的所有模块，确保matplotlib已经安装成功。
  

---

3、用线性回归找到最佳拟合曲线

　　这里给出机器学习实战中文版、英文版以及源代码下载链接。
　　回归的目的是预测数值型的目标值。这里只总结python实现代码（一定是因为公式太难敲），算法介绍还是去看书好不啦。

#加载数据集
def loadDataSet(fileName):      #general function to parse tab -delimited floats
    numFeat = len(open(fileName).readline().split('\t')) - 1 #get number of fields 
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr =[]
        curLine = line.strip().split('\t') #得到每行，并以tab作为间隔
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))
    return dataMat,labelMat

#计算回归系数
def standRegres(xArr,yArr):
    xMat = mat(xArr); yMat = mat(yArr).T
    xTx = xMat.T*xMat
    #采用numpy中的线性代数库linalg，其中linalg.det直接可以计算行列式
    if linalg.det(xTx) == 0.0:
        print "This matrix is singular, cannot do inverse"
        return
    #求回归系数
    ws = xTx.I * (xMat.T*yMat)
    return ws

　　使用loadDataSet()将从数据中得到两个数组，分别存放在x和y中。与分类算法中的类别标签类似，这里的y是目标值。

>>>import regression
>>>from numpy import *
>>>xArr,yArr=regression.loadDataSet('ex0.txt')
>>>ws=regression.standRegres(xArr,yArr)

　　看一下standRegres()函数的执行效果：

>>>ws
matrix([[3.00774324],
[1.69532264]] )

　　变量ws存放的就是回归系数。为了和真实的y值yMat区分开来，将预测出的的y记为yHat 。

>>> xMat=mat(xArr)
>>> yMat=mat(yArr)
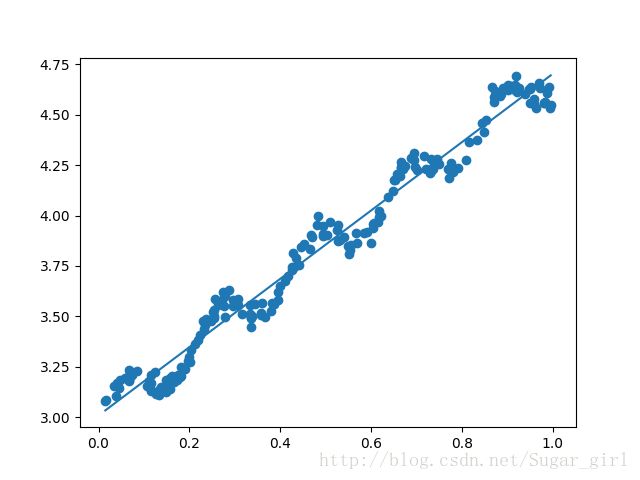
>>> yHat=xMat*ws

　　绘出数据集散点图和最佳拟合直线图：

>>>import matplotlib.pyplot as plt
>>>fig=plt.figure()
>>>ax=fig.add_subplot(111)  
>>>ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0])

　　上述命令创建了图像并绘出了原始的数据。为了绘制计算出的最佳拟合直线， 需要绘出yHat的值。如果直线上的数据点次序混乱，绘图时将会出现问题，所以首先要将点按照升序排列：

>>>xCopy=xMat.copy()
>>>xCopy.sort(0)
>>>yHat=xCopy*ws
>>>ax.plot(xCopy[:,1],yHat)
>>>plt.show()

　　当当当当~第一次用python程序运行出来图有点小激动，想起了某大神用python做数学建模的故事，只可惜没有任何成绩呀（来自一等奖对优秀奖的水包轻踩）

　　在python中 ，NumPy库提供了相关系数的计算方法：可以通过命令 corrcoef(yEstimate,yActual)来计算预测值和真实值的相关性。

>>> yHat=xMat*ws
>>> corrcoef(yHat.T,yMat)

　　该矩阵包含所有两两组合的相关系数。可以看到，对角线上的数据是1.0，因为yMat和自己的匹配是最完美的，而yMat和yHat的相关系数为0.98。

4、局部加权线性回归

　　线性回归的一个问题是有可能出现欠拟合现象，因为它求的是具有最小均方误差的无偏估计 。显而易见，如果模型欠拟合将不能取得最好的预测效果。所以有些方法允许在估计中引人一些偏差，从而降低预测的均方误差。
　　局部加权线性回归（LocallyWeightedLinearRegression, LWLR)。在该算法中，我们给待预测点附近的每个点赋予一定的权重。然后，算法原理还是去看书哦~
　　LWLR使用“核”来对附近的点赋予更高的权重，高斯核公式包含一个需要用户指定的参数k，它决定了对附近的点赋予多大的权重，这也是使用LWLR时唯一需要考虑的参数。python代码实现：

def lwlr(testPoint,xArr,yArr,k=1.0):
    xMat = mat(xArr); yMat = mat(yArr).T
    m = shape(xMat)[0]
    weights = mat(eye((m)))  #创建对角矩阵
    for j in range(m):       #next 2 lines create weights matrix
        diffMat = testPoint - xMat[j,:]  #权重值大小以指数级衰减，输人参数k控制衰减的速度
        weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2))
    xTx = xMat.T * (weights * xMat)
    if linalg.det(xTx) == 0.0:
        print "This matrix is singular, cannot do inverse"
        return
    ws = xTx.I * (xMat.T * (weights * yMat))
    return testPoint * ws
#用于为数据集中每个点调用lwlr(),这有助于求解k的大小。
def lwlrTest(testArr,xArr,yArr,k=1.0):  #loops over all the data points and applies lwlr to each one
    m = shape(testArr)[0]
    yHat = zeros(m)
    for i in range(m):
        yHat[i] = lwlr(testArr[i],xArr,yArr,k)
    return yHat

　　这里选取k为0.01、0.003分别求得结果，采用Matplotlib绘图直观的表示：

>>>import regression
>>>from numpy import *
>>>xArr,yArr=regression.loadDataSet('ex0.txt')
>>>yHat=regression.lwlrTest(xArr,xArr,yArr,0.003)
>>>xMat=mat(xArr)
>>>srtInd=xMat[:,1].argsort(0) #按升序排序，返回下标
>>>xSort=xMat[srtInd][:,0,:] #将xMat按照升序排列
>>>import matplotlib.pyplot as plt
>>>fig=plt.figure()
>>>ax=fig.add_subplot(111)
>>>ax.plot(xSort[:,1],yHat[srtInd])
>>>ax.scatter(xMat[:,1].flatten().A[0],mat(yArr).T.flatten().A[0],s=2,c='red')
>>>plt.show()

　　k = 0.01，0.003对应结果：


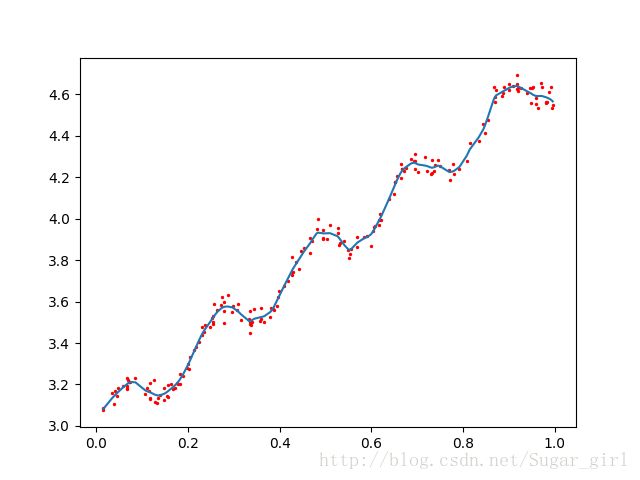
　　可以看到，k=1.0时的模型效果与最小二乘法差不多，k=0.01时该模型可以挖出数据的潜在规律，而k=0.003时则考虑了太多的噪声，进而导致了过拟合现象。局部加权线性回归也存在一个问题，即增加了计算量，因为它对每个点做预测时都必须使用整个数据集。

5、岭回归

　　简单说来，岭回归即是在矩阵xTx上加入一个λI从而使得矩阵非奇异，进而能对矩阵xTx+λI求逆。其中矩阵I是一个单位矩阵，即对角线上元素皆为1，其他均为0。而λ是一个用户定义的数值。
　　岭回归最先用来处理特征数多于样本数的情况，现在也用于在估计中加人偏差，从而得到更好的估计。这里通过引入λ来限制了所有w之和，通过引人该惩罚项，能够减少不重要的参数，这个技术在统计学中也叫做缩减（shrinkage )。

#@lam：惩罚项系数lambda，默认值为0.2
def ridgeRegres(xMat,yMat,lam=0.2):#用于计算回归系数
    #计算矩阵内积
    xTx = xMat.T*xMat
    #添加惩罚项，使矩阵xTx变换后可逆
    denom = xTx + eye(shape(xMat)[1])*lam
    #判断行列式值是否为0，确定是否可逆
    if linalg.det(denom) == 0.0:
        print "This matrix is singular, cannot do inverse"
        return
    #计算回归系数
    ws = denom.I * (xMat.T*yMat)
    return ws

#特征需要标准化处理，使所有特征具有相同重要性    
def ridgeTest(xArr,yArr):#用于在一组λ上测试结果
    xMat = mat(xArr); yMat=mat(yArr).T
    #计算均值
    yMean = mean(yMat,0)
    yMat = yMat - yMean     #to eliminate X0 take mean off of Y
    #regularize X's
    xMeans = mean(xMat,0)   #calc mean then subtract it off
    #计算各个特征的方差
    xVar = var(xMat,0)      #calc variance of Xi then divide by it
    #特征-均值/方差
    xMat = (xMat - xMeans)/xVar
    #在30个不同的lambda下进行测试
    numTestPts = 30
    #30次的结果保存在wMat中
    wMat = zeros((numTestPts,shape(xMat)[1]))
    for i in range(numTestPts):
        #计算对应lamda回归系数，lamda以指数形式变换
        ws = ridgeRegres(xMat,yMat,exp(i-10))
        wMat[i,:]=ws.T
    return wMat

　　代码中用到NumPy库中的eye()方法来生成单位矩阵；
　　代码中仍保留了判断行列式是否为0的代码，原因是当λ取值为0时，又回到了普通的线性回归，那么矩阵很可能出现不可逆的情况；
　　岭回归中数据需要进行标准化处理，即数据的每一维度特征减去相应的特征均值之后，再除以特征的方差；
　　这里，选择了30个不同的λ进行测试，并且这里的λ是按照指数级进行变化，从而可以看出当λ非常小和非常大的情况下对结果造成的影响。

import regression
from numpy import *
abX,abY=regression.loadDataSet('abalone.txt')
ridgeWeights=regression.ridgeTest(abX,abY)

　　这样就得到了30个不同lambda所对应的回归系数。为了看到缩减的效果，在Python提示符下输入如下代码：

>>>import matplotlib.pyplot as plt
>>>fig=plt.figure()
>>>ax=fig.add_subplot(111)
>>>ax.plot(ridgeWeights)
>>>plt.show()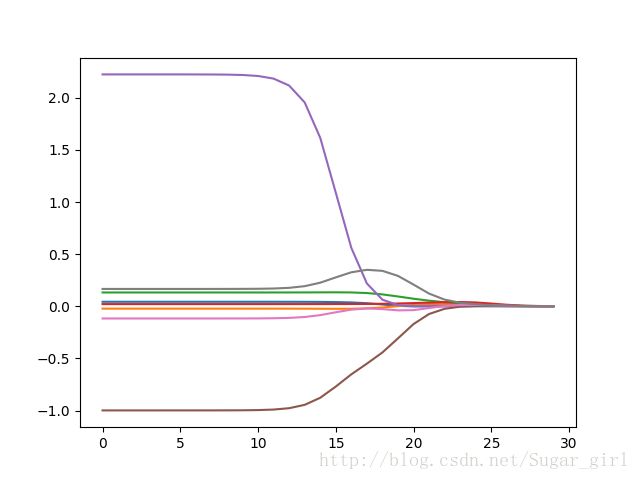

　　该图绘出了回归系数与log(λ)的关系， 为岭回归的回归系数变化图。λ非常小时，系数与普通回归一样。而λ非常大时，所有回归系数缩减为0。可以在中间某处找到使得预测的结果最好的λ值。

6、前向逐步回归

　　前向逐步回归是一种贪心算法，即每一步都尽可能的减小误差。一开始，所有的权重都设为1，然后每一步所做的决策是对某个权重增加或减少一个很小的数值。算法的伪代码为：

 数据标准化，使其分布满足0均值和单位方差
 在每轮的迭代中：
     设置当前最小的误差lowestError为正无穷
     对每个特征：
         增大或减小：
             改变一个系数得到一个新的w
             计算新w下的误差
             如果误差Error小于当前最小的误差lowestError：设置Wbest等于当前的w
         将w设置为新的Wbest
     将本次迭代得到的预测误差最小的w存入矩阵中 返回多次迭代下的回归系数组成的矩阵