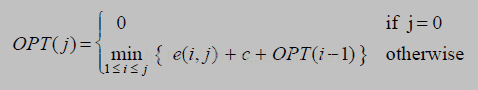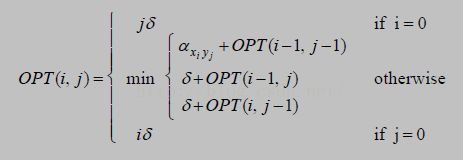算法总结1——贪婪算法,动态规划
该文章所用的图片取自上海交大电院高晓沨老师上课所用的课件~顺便说一句,高老师的英语简直太棒了!
网址:http://cs.sjtu.edu.cn/~gao-xf/algorithm/
正值期中,即将考试,总结一下之前学的算法还是很有必要的,一方面记录以备之后用到,一方面防止自己在复习的过程中走神...之前做笔记总是想着自己看懂就好,其实很多地方没有写明白,导致之后看起来还是比较费力的,而目前任务多又重(估计之后也好不到哪里去),只想能不动脑就不动脑啊。所以想让自己写出的东西通俗易懂,方便查阅。
算法其实很简单,只是有时候一个变量或者定义没有搞清楚导致一环一环接不上就会以为它很难,多请教自然就明朗啦~很多事情其实没有那么复杂,只是因为你不知道而已。写下这句仅为提醒自己克服对未知的恐惧。
1、贪婪算法
基本都要先排序,从排序的开始那个依次判断,符合就留下不符合就去掉。
间隔调度Interval Scheduling
input:开始时间:Sj 结束时间:Fj
requirement:两个工作不能重叠

最早开始时间——按照Sj排序
最早结束时间——按照Fj排序
最短间隔(所有工作(结束时间 - 开始时间)最短的最大集合)——按照(Sj - Fj)排序
最少冲突(选择的工作与其他没选择的工作冲突最少的最大集合)——找到每个工作 j 与其他工作冲突的个数Cj,按照Cj排序
好像最早结束时间是最好的,为什么呢0.0
其实以上四个概念还有比较模糊的地方,之后补全
间隔分区Interval Scheduling
input:开始时间:Sj 结束时间:Fj
requirement:找到最少的分区,使得所有工作都能完成并且没有冲突
从图中我们可以看出,第二种明显好于第一种。so, classroomNumber >= depth(depth就是我们要求的最小的分区数)
算法:
1、根据开始时间排序
2、从第一个开始找,与之前的k个classroom比较,如果有时间不冲突的,就放在这里,如果冲突就新建一个classroom
时间复杂度:O(n log n)-------(排序:O(n log n),后边:O(n),所以总的是:O(n log n))
最少迟到安排Scheduling to Minimizing Lateness
input:工作时间:Tj 规定的结束时间:Dj
requirement:一次只能完成一个工作,调度所有工作使得迟到的时间最小化

1、最小工作时间优先:按照Tj升序
2、最小松弛时间优先:按照Dj-Tj 升序
3、最早deadline优先:按照Dj升序
好像最早开始时间最好,为什么呢0.0
最优离线缓冲Optimal Offline Caching
input:
requirement:
解释:
左图——每行向下时间递增,缓冲只有三个,第一次找到了a,第二次又找到了a,然后除了a其他随意找一个元素替换(把b换成了x),下次再找,再换~~~
右图——每行向下时间递增,缓冲只有三个,有的时候就会遇到找不到的情况,那就换,比如首先遇到的是找不到d了,那就把d加进来
选择断点Selecting Breakpoints
input:断点:{b0,b1,b2,...,bn} 加满油能跑的距离:C
requirement:跑完全程,停车加油次数最少
算法:
解释:
首先按照断点的大小排序
找到编号最大的断点,满足目前的位置加C能到该断点。如果有则选择bp,如果没有则返回没有解决方案。
时间复杂度:O(n log n)
兑换硬币Coin Changing
input:硬币:1,5,10,100 总兑换钱数:N
requirement:找的硬币数最少
算法“:
解释:
硬币排序
从最大的开始,如果钱数大于最大的硬币就继续地找最大的硬币,如果钱数小于最大的硬币面额,就找比它小的硬币里最大的
但是找硬币并不是对任何序列都有效的。
比如:,6, 34, 70, 100这个组合找140——100, 34, 6,而最优是70, 70
最小生成树Minimum Spanning Tree
input:图G=(E,V)
requirement:使生成树的边和最小
解释:边升序
如果选了一条边,如果有一个与该边相关联的顶点在顶点集中,则把相关联的顶点从顶点集去掉,把边加到结果集中,直至结束。
聚类Clustering
input:顶点集,类别数:K
requirement:使每类距离最小
等价于寻找最小生成树,删掉距离大的K条边。
2、动态规划Dynamic programming.
Break up a problem into a series of overlapping sub-problems, and build up solutions to larger and larger sub-problems.
把一个问题分为一系列重叠的子问题,建立解决方案解决越来越大的子问题。
其实简单来说就是建立一个表(咱不聊递归,如果效率还可以,我是绝对不会考虑它的,没有为什么,就是内心的恐惧),每次往里边加一个元素,用到之前表里边记录的数据算下一个呗。
以下有几个常用的算法,有时间可以查下,暂时就不讲了哈~
Unix diff 用于比较两个文件
Viterbi 用于隐式马尔科夫模型
Smith-Waterman 用于基因序列对齐
Bellman-Ford 用于寻找网络中的最短路径
Cocke-Kasami-Younger 用于前后文无关的语法分析
加权间隔调度Weighted Interval Scheduling
input:开始时间:Sj 结束时间:Fj 权重:Vj
requirement:两个工作不能重叠
goal:找到权重最大的互相兼容的工作
如果使用贪婪算法:
1、将所有的工作按照结束时间排序 2、如果该工作和之前选择的工作不冲突,则加到结果集合中
但是如果加了权重,那么贪婪算法就会失效
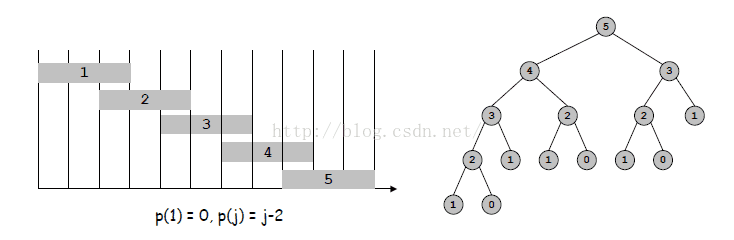
动态规划之加权间隔调度——蛮力法
1、将所有工作按照结束时间排序
定义:P(j)=和工作j兼容的最大的工作i
定义:OPT(j)=对于工作j来说最优的权重和(区间为从1到j)
2、
解释:①、如果 j 为0,则权重和为0 ②、如果j不为0,比较如果选 j(权重和为 j 的权重Vj + 在 j 之前且和 j 最大兼容的工作的最优权重和)和如果不选j(j-1的最优权重和)两种情况,选择权重和大的那一个作为 j 的最优权重和
我们可以看出在上边蛮力法的图中,有很多重叠的区域,比如2-(1,0)重复了3次,3-(1,(2-1,0))重复了2次。这种情况下重复计算明显是可以避免的,因此我们设置一个数组,用来记录这些情况。
时间复杂度为O(n logn)
动态规划之加权间隔调度——自底向上(no 递归)
分段最小二乘(Segmented Least Squares)
input:所有点的坐标(xj,yj)
requirement:找到一组线,使得 1、所有点到线的距离平方和E最小 2、线的数量L最小——可以合并为E+cL(c>0)最小
定义:
OPT(j)=对于p1,p2,...,pj来说最小cost
e(i,j)=p(i),p(i+1),...pj最小平方和
公式:
解释:
如果j=0,则最小cost就是0
否则,i 与之后一直到 j 所有的点拟合一条新的线的cost + 新增加了一条线就会多出的代价C + i 点之前的最小平方和OPT(i-1)
算法:
时间复杂度O(n^3)
背包问题Knapsack Problem
input:各个物品对应的weight和value
requirement:重量(weight)有限制的情况下,如何选择价值和(value)最大的物品
定义:
OPT(i,w)=从1到 i 的物品的最大价值和(在重量W内)
公式:
解释:
如果i=0,则从1到 i 的最大价值和为0
如果 i 的重量大于总的重量,则 (从1到 i 的最大价值和) = (从1到 i -1的最大价值和)
其他情况,选 (第i-1个物品重量为W的价值和) 与 (第i个物品的value+之前物品(重量为w-wi)最优价值和)中最大的一个作为(从1到 i 的最大价值和)
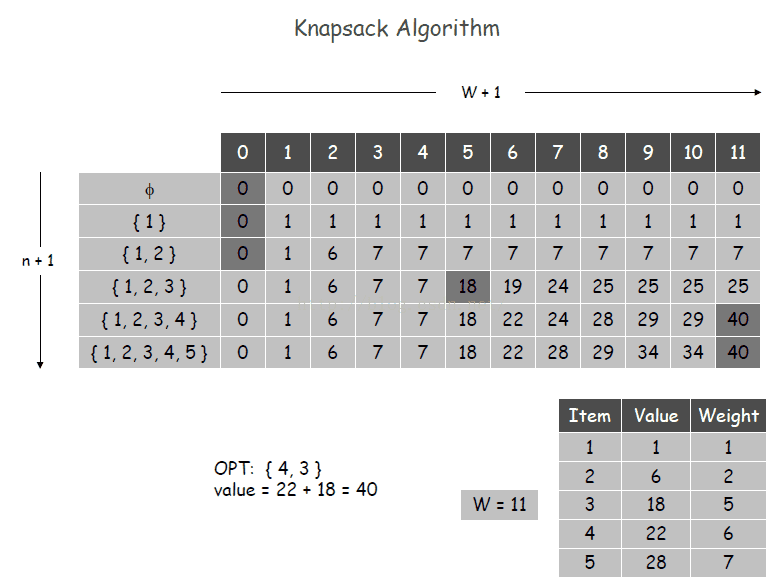
算法——自底向上(no 递归)
示例
时间复杂度:
O(n*W)
RNA二级结构RNA Secondary Structure
input:ACGU序列
requirement:1、AU配对 CG配对 2、如果有拐角,中间间隔至少4个元素 3、不可以穿插
定义:
OPT(i,j)=从 i 到 j 碱基对的最大数量。
解释:
1、如果 i >= j-4,则OPT(i,j)=0
2、如果 bj不和哪个元素配对,则OPT(i,j)=OPT(i,j-1)
3、如果 bj 和 bt 配对,并且 i <= t <= j-4,则OPT(i,j)=1+max{ OPT(i,t-1) + OPT(t+1, j-1) }——最前边加的那个1,就是 bj 与 bt 配对的那一对的计数
时间复杂度O(n^3)
编辑距离Edit Distance
input:两个字符串A,B
output:他们之间的距离(插入、删除、替换的总次数)
定义:OPT(i,j) = 字符串a1,a1,...,ai 与b1,b2,...,b j 的最小距离
上图是PPT中的公式,但是alpha是神马意思我就不造了,所以写了下边这个公式没有那么多符号,直观一点咯:
首先先把第0行和第0列初始化为0,1,2,3,.....,n(是和字符串相关的,比如A有2个字符,那么它的n=2;如果B有3个字符,它的n=3)
OPT(i,j)=
(1) OPT(i-1,j-1) if ai==bj
(2) 1 + min{OPT(i-1,j-1), OPT(i-1,j), OPT(i,j-1)} if ai !=bi
解释:
如果ai = bi,那么这一对就不必参与计数,直接拿到去掉他们两个的最小cost就好
如果ai != bi,那么就看一下(去掉他们两个,或者去掉他们其中某一个)这三种情况中哪种的cost最小,那就取这个cost再把由于它们的增加而带来的那个 1 加上
实例:
a c h d f f
0 1 2 3 4 5 6
a 1 0 1 2 3 4 5
b 2 1 1 2 3 4 5
c 3 2 2 2 3 4 5
d 4 3 3 3 2 3 4
e 5 4 4 4 3 3 4
f 6 5 5 5 4 3 3
g 7 6 6 6 5 4 4
以行或者列开始循环都可以,两个for就搞定,时间为O(n^2)