对偶和KKT条件

前言：

对偶（duality）是优化中的一个很重要的一点，以对偶问题的特性为根本的KKT条件，在很多优化问题的求解上行之有效。本文简要介绍对偶问题的基本概念和核心技术以及KKT求解的原理和方法。

什么是对偶？

对偶问题，就是将原问题（primal problem）转化为对偶问题（dual problem）然后在进行求解的方法。

详细解说对偶

1. 优化问题可以表示为：

minf0(x)
s.t.fi(x)<=0i=1,2,...n;hj(x)=0j=1,2,...m

如果n,m都是0，优化问题为无约束优化问题（无优化问题的对偶问题就是自己），如果n=0，则为等式约束问题。

优化问题的定义域 D为所有函数定义域的交集。

2.一个优化问题的对偶问题可以这样得到：

1.首先写出拉格朗日函数
L(x,u,v)=f0(x)+∑n1ui∗fi(x)+∑m1vjhj(x)
其中 u,v 为拉格朗日乘数，也叫对偶变量，顾名思义， u,v 是对偶问题中的变量。
2. 拉格朗日函数逐点对x求下确界得到对偶函数
g(u,v)=infx∈DL(x,u,v)=infx∈Df0(x)+∑n1ui∗fi(x)+∑m1vjhj(x)
其中下确界指最大的下届，也就是最小值。逐点对x求下确界意味着，对任意一个 u,v 求出一个x使 L(x,u,v) 最小。如果把 u,v 当成变量，x当成参数，那么不论x取什么值，L都是一个仿射函数

L(X,u,v)=A∗u+B∗v+C ,其中
A=(f1(X),f2(X),...,fn(X))
B=(h1(X),h2(X),...,hm(X))
C=f0(X)

3.对偶问题是凹的

那么 g(u,v) 为很多个仿射函数的逐点取最小值，而这样得到的函数一定是凹的。可以参照下图理解。


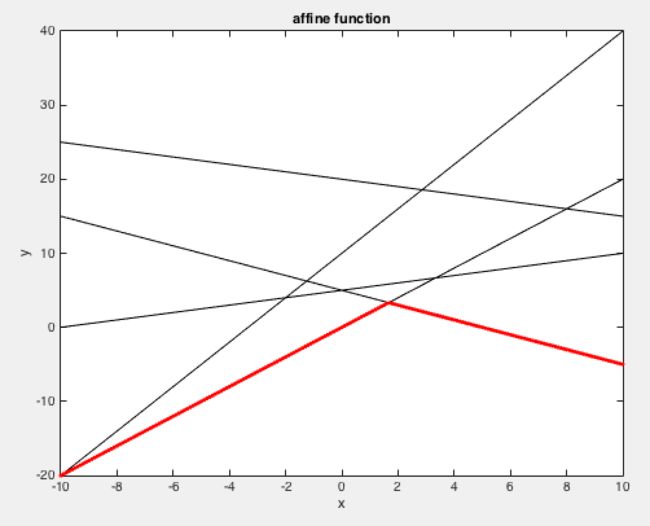
红色的线为逐点取最小值得到的函数图像。

这便是为什么要有对偶算法这个算法的一个原因，因为对偶问题都是凸问题（其实是凹问题，凹问题加个负号就是凸问题了），而凸优化问题在求解上会简单很多。一般而言，如果可以把一个问题表述成凸优化问题，那么就相当于基本解决了这个问题。

4. 原问题与对偶问题的关联

4.1 原问题的最小值大于或等于对偶问题的最大值。
f∗=minx∈Dands.t.f0(x)>=fx(x)>=L(x,u,v)>=g(u,v)
对任意 u,v 都有 g(u,v)<=f∗ 所以 g∗=maxu,vg(u,v)<=f∗

4.2 原问题最小值和对偶问题的最大值之差 叫 duality gap（我还不知道改如何翻译成中文）
△=f∗−g∗
如果 △=0 就是强对偶，否则就是弱对偶，那么什么时候弱什么时候强呢？
4.3 如果满足原问题是凸优化问题，并且至少存在绝对一个绝对可行点（什么叫绝对可行点，就是一个可以让所有不等式约束都不取等号的可行点），那么就具有强对偶性。这个条件就是传说中的Slater’s condition。
4.4 由此可知一个只有等式约束的凸优化问题和其对偶问题一定具有强对偶性，因为根本就没有不等式约束（推论）。
5.5 既然只有强对偶条件时才能保证对偶问题的最大值是原问题的最小值，那对偶法还有用吗？

KKT condition

当然有用，KKT condition 就是对偶性质的一个应用。
f∗>=g∗ ，那么如果存在 x,u,v ,使 f∗=g∗ （不一定要计算出来，只要说明相等就行）那么，此时 x,u,v 就分别是原问题和对偶问题的最优解。那么我们就可以以这个为条件作为约束求出最优解。怎么利用这个条件呢？推一推(参考CMU教程)

f(x∗)=g(u∗,v∗)=minxL(x,u∗,v∗)<=L(x∗,u∗,v∗)<=f(x∗)
可知所有等号都成立
f(x∗)=g(u∗,v∗)=minxL(x,u∗,v∗)=L(x∗,u∗,v∗)=f(x∗)

即如果存在 x,u,v 使
1. ∂L(x,u,v)∂x=0(fromminL(x,u,v))
2. vj∗hj=0(fromL(x∗,u∗,v∗)=f(x∗))
3. fi<=0,hj=0(原问题的可行域)
4. vj>=0(对偶问题的可行域)

如果存在 x,u,v 满足上面四个条件，那么他们就是原问题和对偶问题的可行解。这就是KKT条件。

而拉格朗日乘数法正是KKT条件在等式约束优化问题的简化版。