字符串模式匹配——KMP

Warning：本文从常见的字符串模式匹配开始，以通俗易懂的语言阐述了KMP算法原理和适用的场景，编写尽量避免使用晦涩的语言及复杂的数学公式，只为作为学习笔记记录个人的理解过程，追求理论的同学请绕行到《算法导论》。
ps：本文是小编一字一字的码出来的，代码是一行一行敲出来的，欢迎转载，但请务必注明出处。

      在开发过程中，经常会遇到字符串模式匹配的问题，即定位一个子串在主字符串中位置，很多高级语言内置了字符串模式匹配的API。比如在JAVA中，java.lang.String提供了indexOf()、lastIndexOf()方法供开发者调用。但是如果不使用JDK内置的模式匹配函数，我们该如何实现一个高效的模式匹配算法呢？从一个简单的示例开始我们的KMP探索之旅。

---

一、简单字符串匹配算法

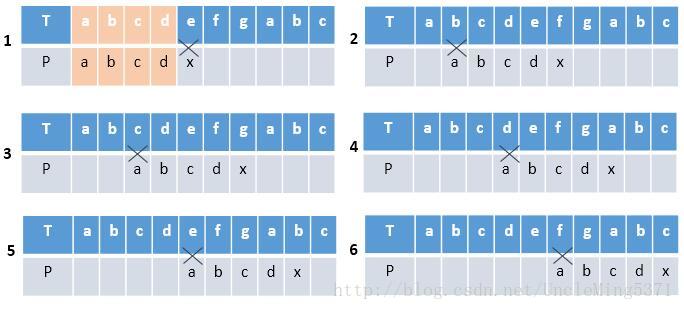
      假设我们要从主串T=”goodgoole”中，找到子串P=”goole”的出现的位置。最基本的思路是：主串T和子串P分别定义游标：i、j，两个游标从0开始移动，逐位进行比较，当某个位置的字符不匹配时，将主串游标i回溯到本次比较开始的下一位，将子串的游标j回溯到0继续比较。步骤如下：

1. i=0；j=0；从主串T的第一位开始，T与S的前三个字符串都匹配成功，但是第四个字符不相等，则主串第一位定位失败。如下图：
   
   此时，游标i从第四个字符位置回溯到第二个字符，游标j从第四个字符回溯到第一个字符。

2. i=1；j=0；从主串T第二位开始比较，T[1] = o , P[0] = g，T[1] != P[0] 。如下图：
   
   子串首位字符与主串第二位字符不相等，向后移动主串的游标i到第三个字符。

3. i=2；j=0；从主串T第三位开始比较，T[2] =o，P[0]=g, T[2] != P[0] 。如下图：
   

4. i=3；j=0；从主串T第四位开始比较，T[3] =d，P[0]=g, T[3] != P[0] 。如下图：
   

5. i=4；j=0；从主串T第五位开始比较，T[5] =d，P[0]=g, T[5] == P[5] 。如下图：
   
   同时移动主串游标i、子串游标j。i = 5、j = 1， T[5]= P[1] ，以此类推，直到 T[9]==P[5]; 比较结束。

      综上所述，简单的说，就是对主串进行大循环，以主串T的每一个字符作为开头与子串的首字符进行比较。如果匹配则同时移动主串游标和子串游标；如果不匹配，则将主串的游标回溯到第一个比较位的下一个位置，子串则回溯到0，进行下一轮比较，直到游标达到边界值为止。

---

代码实现如下：

    /**
     * 简单的字符串模式匹配
     * @param target    目标字符串
     * @param pattern   模式字符串
     * @return
     */
    int simpleIndex(String target, String pattern) {
        int i=0, j=0;   //i:主串游标、j:子串游标

        while(i < target.length() && j < pattern.length()) {
            if(target.charAt(i) == pattern.charAt(j)) {
                i++;
                j++;
            } else {
                i = i-j+1;
                j=0;
            }
        }

        if(j == target.length()) {
            return i-target.length();
        } else {
            return -1;
        }
    }

      分析一下上面的算法时间复杂度，最好的情况就是一开始就匹配成功，比如主串为“hello world”，长度为n，子串“hello”，长度为m，时间复杂度为O(m)；最坏的情况比如主串为“00000000000001”，子串为”000001“，则时间复杂度为O((n-m+1)*m)。可见这种算法的效率非常低下，我们把这种算法称之为”简单字符串匹配算法“。

---

二、KMP算法

      通过前面介绍的简单字符串匹配算法时间复杂度发现，这种算法之所以低效是因为不断的回溯游标，逐位进行比较，这是非常糟糕的。大牛们不甘忍受这种低效的匹配算法，在想如果想提高算法的效率，有没有可以减少游标回溯的方法呢？于是有三位前辈：克努特、莫里斯、普拉特发表了一个高效的模式匹配算法——KMP算法。

为了将讲清楚KMP算法，我们从两个示例开始，比较KMP算法与朴素匹配算法。

示例一

      如果主串为”abcdefgabc“，要匹配的子串为”abcdx“，如果按照朴素匹配算法，则实现步骤如下：

      主串前四位与子串的前四位匹配成功，直到第五位e与x不匹配，则移动主串的游标到第二位，与子串首位进行比较，以此类推：2、3、4、5、6步骤比较的结果都是首位字符不匹配。仔细分析发现，对于要匹配的子串P=”abcdx“，首位字符a与之后的任意一位字符都不相等，而主串和子串的前四位完全匹配，则意味着P的首位不可能与主串的2、3、4位字符相等，当第五位字符不相等时，则不需要用子串的首位与主串的2、3、4位进行比较，由此可见，上图中2、3、4步骤可以跳过，这是理解KMP算法的关键。

---

示例二

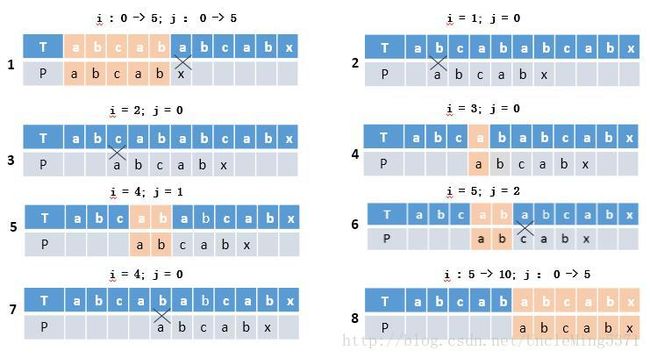
      示例一的特殊性在于要匹配的子串P=”abcdx”中不包含重复的字符串，如果待匹配的字符串中包含重复的字符该如何处理呢？如果主串为”abcababcabx“，要匹配的子串为”abcabx“，如果按照朴素匹配算法，则实现步骤如下：

      在步骤1中，主串T的前五位与子串的前五位匹配，第六位不匹配，则回溯主串的指针到第二位字符，与子串的第0位开始比较。到步骤4时，主串的第4位、第5位字符与子串的前两位匹配，第6位字符与子串的第三位不匹配，则继续回溯指针，直到指针达到边界值位置。

      首先分析子串Ｔ＝”abcabx”，前两位ab与四五位ab相同。在步骤1中，主串前五位与子串前五位匹配，但是T的首位a与自身的第二位第三位不匹配，则子串的首位与主串的第二、三位一定不匹配，所以第2、3步骤是多余的操作。

      在步骤4中首先比较用主串的第四个字符a与子串的第0个字符a比较（a==a）；步骤5中用第五个字符b与子串第一个字符b比较（b==b）；步骤6中第六个字符（a）与子串第三个字符（c）比较（a！=c），则比较结束。但是我们通过步骤1可知，子串的第四个字符与第五个字符和主串第四个字符与第五个字符相等，同时子串的第四个字符和第五位字符与自身第一个和第二个位字符相等，则步骤4、步骤5不需要比较可以跳过，直接比较步骤6即可。

      在步骤7中，通过步骤1、步骤6都可得出，主串第5个字符b与子串第二个字符相等，而子串第2个字符与自身第1个字符不相等，则主串第5个字符一定与子串第1个字符不相等，可以第步骤7也是多余的操作。

      通过上面的两个示例分析发现，去掉多余的比较步骤之后，主串的游标i没有任何回溯操作。如在示例1中，去掉多余的步骤2、3、4之后，游标i=4与子串的游标j=0进行比较；在示例2中，去掉多余的步骤2、3、4、5、7之后，游标i没有回溯。而对于游标j，在示例一中每次回溯到0，在示例二中每次回溯的位置取决于自身当前位置前面字符与自身开头字符的匹配程度，如在步骤1中，第6个字符x与主串不相等，而第6个字符前面有2个字符与自身开头匹配，跳过多余的步骤2、3、4、5，在第六步骤中，直接用第三个字符（即j=2）与主串比较，当第3个字符c（j=2）与主串第6个字符a（i=5）不相等时，第三个字符串前面字符与开头字符不相等，则j回溯到0。因此，子串游标j的回溯程度与自身字符的重复程度有关，有主串无关。

      这就是KMP算法的核心思想：避免不必要的回溯，主串游标不进行回溯，子串游标在每个位置的回溯位数与当前位置之前字符与自身开始几位的字符匹配程度来决定。在实现一个KMP的算法关键，是推导出待匹配的字符串（即子串）各个位置应该回溯到的位置，我们把各个位置放到一个next数组中。

---

推导next数组

例1
如果待匹配子串P=”abcde”，按照如下步骤推导：
(1) 当 j = 0 时，记为-1（特殊标记，代码实现时当回溯到 j = 0时，回溯结束）next[0] = -1;
(2) 当 j = 1 时，前面只有一个字符a，则next[1] = 0;
(3) 当 j = 2 时，前面有两个字符a和b，a ！= b， 则next[2] = 0;
(4) 当 j = 3 时，前面字符串abc，无相等字符，则next[3] = 0;
以此类推，最后推导出数组next = { -1, 0, 0, 0, 0, 0 }

例2
如果待匹配子串为P=”abcabx”（示例二中的子串），按照如下步骤推导：
(1) 当 j = 0 时，next[0] = -1;
(2) 当 j = 1 时，前面只有一个字符a，则next[1] = 0;
(3) 当 j = 2 时，前面有两个字符a和b，a ！= b， 则next[2] = 0;
(4) 当 j = 3 时，前面字符串abc，无相等字符，则next[3] = 0;
(5) 当 j = 4 时，前面字符abca，第4位字符与首位相等，则next[4] = 1;
(6) 当 j = 5 时，前面字符abcab，第4、5位字符与第1、2位相等，则next[4] = 2;
以此类推，最后推导出数组next = { -1, 0, 0, 0, 1, 2 }

      通俗的说，就是当前位置之前有几个连续字符与开头的连续字符相等，则回溯位置记为相等的字符数。用例2推导出的next数组，结合示例二验证next数组是否正确，示例二的步骤1中i = 5，j = 5，此时T[i] != T[j]，则回溯j的位置，回溯到的位置即next[5] = 2，跳过多余的步骤2、3、4、5，在第六步中j = 2开始比较。而例1中j则每次都回到第0位开始比较，大家可以结合示例1自行验证。

---

KMP算法代码（Java版）

KMP算法的关键是推导出next数组（即待匹配字符串各个位置的回溯位置），推导代码如下：

int[] getNext(String pattern) {
        int[] next = new int[pattern.length()];
        next[0] = -1;
        int i=0, j=-1;

        while(i < pattern.length()-1) {
            if(j == -1 || pattern.charAt(i) == pattern.charAt(j)) {
                i++;
                j++;
                next[i] = j;
            } else {
                j = next[j];
            }
        }

        return next;
    }

有了上面推导next数组的结果，KMP匹配算法代码如下：

    /**
     * KMP匹配字符串
     * @param source  源字符串
     * @param subStr  模式字符串
     * @return
     */
    int kmpIndexOf(String target, String pattern) {
        int[] next = getNext(pattern);
        int i=0, j=0;

        while(i < target.length() && j < pattern.length()) {
            //j==-1是关键，表示已经回溯到了第0位，这就是在上面推导next数组时使用-1的原因
            if(j==-1 || target.charAt(i) == pattern.charAt(j)) {
                i++;
                j++;
            } else {
                j = next[j];
            }
        }

        if(j >= target.length()) {
            return i - target.length();
        }

        return -1;
    }

      KMP算法的代码实现与前面简单字符串匹配算法比较，改动并不大，增加了j==-1的判断，并增加了j =next[j]（回溯到合适的位置），但是整个算法的时间复杂度变成了O(n+m),相比较于简单字符串匹配模式时间复杂度O((n-m+1)*m)要好很多。

---

三、总结

      KMP算法通过避免主串和子串位置的回溯，提高了算法的时间效率。但是如果主串是”abcdef“，子串是”123456“，则主串游标i、子串游标j的移动步骤与简单字符串相同，如果使用KMP算法还需要推导next的时间消耗，此时KMP算法效率低于简单字符串。但是KMP算法并不是一个银弹，它的适用场景是待匹配的子串与主串存在大量重复匹配的字符时，算法的高效才得以体现。