哈夫曼树（huffman）

一、为什么需要哈夫曼树？

      在实际开发过程中，我们常常会用到大量的条件判断，这些条件判断直接影响着程序的执行效率。比如我们在一个将分数转换成等级的程序中，很容易想到使用如下的代码来实现：

if(score < 60) {
    return "不及格";

} else if(score < 70) {
    return "及格";

}else if(score < 80) {
    return "中等";

}else if(score < 90) {
    return "良好";

} else {
    return "优秀";

}  

      分析上面的程序的时间消耗，则可能会发现程序的缺陷。程序的时间消耗与score的分布相关，在两种极端情况下，如果score全在60以下，则每个score只需要一次比较即可；如果score全在90分以上，则每个score的结果需要经过4次比较才能返回结果，时间差异较大，因此在比较过程中我们考虑将各个score范围。按照预先设定的比例进行排序，将比例较高的放到前面，占比较小的放到后面，这样可以在一定程度上减少比较次数。假设我们已知各范围分数占比如下：

      按照上面假设的比重可以发现70分以上的比重占了80%，不过按照如上的程序需要通过三次的判断才能到达，70~79分占的比重最高，占了40%，不及格所占的比例最少，我们根据比例的多少重新构建二叉树。
      为了更直观的比较，我们首先对为优化之前的程序构建一棵二叉树，如下图：

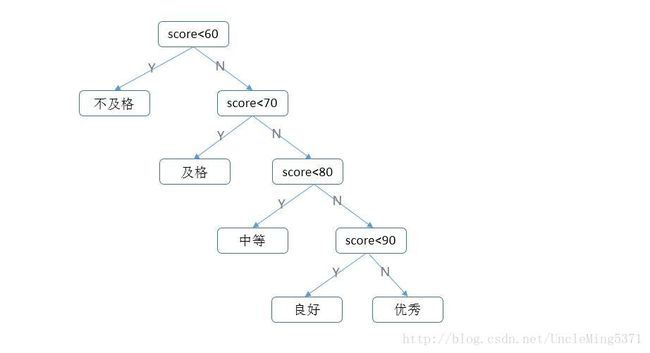
按照各分数比重优化之后的二叉树，如下图：

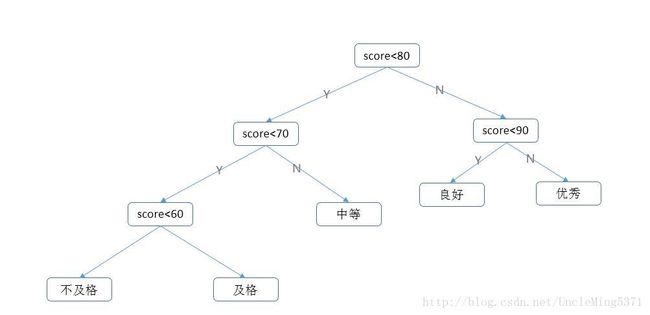
      对比两种结构，显然第二种结构的判定效率更高。那么第二种结构是不是效率最高的呢？我们该如何去设计一棵效率最优的二叉树呢？ 我们把这种效率最高的二叉树称为“最优二叉树”，也称“哈夫曼树（huffman)”。

---

二、哈夫曼树的定义与原理

我们把上面这两棵树简化成叶子节点带权值的二叉树（节点间的边的相关数叫做权weight）。

百度百科关于权值的解释如下：
权值就是定义的路径上面的值。可以这样理解为结点间的距离。通常指字符对应的二进制编码出现的概率。
至于哈夫曼树中的权值可以理解为：权值大表明出现概率大！
一个结点的权值实际上就是这个结点子树在整个树中所占的比例。

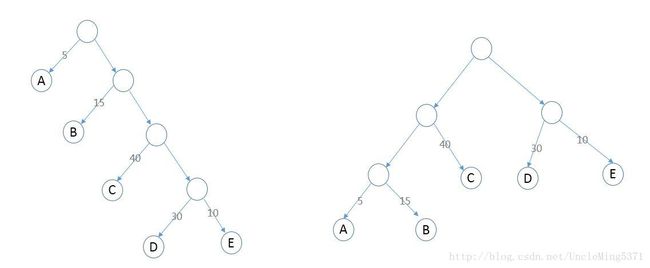
      如上图所示。A表示不及格、B表示及格、C表示中等、D表示良好、E表示优秀，其中每个分支线上的数字就是我们在前面提到的各个成绩所占的百分比。

哈夫曼树相关概念：
1. 路径长度：从树中一个节点到另一个节点之间的分支构成两个节点之间的路径，路径上分支数目称为路径长度；
2. 树的路径长度：从根节点到每一个子节点的路径长度之和。
3. 节点带权路径长度：从当前节点到根的路径长度乘以节点的权值。
4. 树的带权路径长度：树中所有叶子节点的带权路径长度之和。
5. 哈夫曼树：假设有n个权值{w1, w2,…,wn}，构造一棵有n个叶子节点的二叉树，每个叶子节点带权值wk，每个叶子节点的路径长度为lk，我们通常记作，其中带权路径WPL最小的二叉树称做”哈夫曼树“，也叫做”最优二叉树“。

      针对上面两个二叉树，我们解释上面提到个各个概念，在左图中，根节点到节点D的路径长度为4，在右图中，根节点到节点D的路径长度为2。左图中树的路径长度为：1+1+2+2+3+3+4+4 = 20，右图中树的路径长度为：1+2+3+3+2+1+2+2=16。
左图中二叉树的WPL = 5 * 1+ 15 * 2 + 40 * 3 + 30 * 4 + 10 * 4 = 315。
右图中二叉树的WPL = 5 * 3 + 15 * 3 + 40 * 2 + 30 * 2 + 10 *2 = 220。
      计算出的这两个结果可以说明什么问题呢？如果我们现在对1000个成绩进行判定，用左图的树进行判定需要3150次，右图需要2200次，可见性能有了很大提升。这样的二叉树又该如何进行构建呢？

三、哈夫曼树的算法

      根据上面介绍的哈夫曼树的定义，要使一棵哈夫曼树的WPL最小，就必须使权值越大的叶子节点越靠近根节点，同时除了带权值的叶子节点外，必须保证其他所有的节点度为2，这样构造出的二叉树便是哈夫曼树。

假如我们有4个节点A、B、C、D，权值分别为：10、5、2、8，我们该如何构建哈夫曼树呢？
       1. 先把这些节点按照权值从小到达进行排序，排序结果为：C（2）、B（5）、D（8）、A（10）；
      2. 取前两个最小权值的节点作为一个新节点N1的两个子节点，注意相对较小的作为左子节点，此时我们取出C（2）、B（5），C作为新节点N1的左子节点，B作为新节点N1的右子节点，如（图一）；
       3. 将N1替换C（2）、B（5），插入到上面的节点排序结果中，继续保持从小到达的顺序。此时排序序列为：N1（7）、D（8）、A（10）；
       4. 重复步骤2。取出N1（7）、D（8）构建新的节点N2，N1为N2的左节点、D为N2的右节点，N2的权值为N1的权值+D的权值=15，如（图二）；
       5. 重复步骤3，将N2插入排序序列，序列为：A（10）、N2（15）；
       6. 重复步骤2。将A（10）、N2（15）取出，构建新的节点N3，A为左子节点、N2为右子节点，此时N3是根节点。如（图三）

通过上面的构造哈夫曼树的步骤，我们总结下哈夫曼算法的思想：
       1. 根据给定的n个权值{W1, W2, …, Wn}构成n棵二叉树的集合F={T1, T2, …,Tn}，其中每棵二叉树Ti中只有一个带权为Wi根节点，其左右子树均为空；
       2. 在F中选取两棵根节点的权值最小的树作为左右子树构造一棵新的二叉树，且把新的二叉树的根节点的权值为其左右子树的根节点的权值之和；
       3. 在F中删除这两棵树，同时将新得到的二叉树加入F中；
       4. 重复上面2、3步骤，直到得到一棵树为止。这棵树便是哈夫曼树。

---

四、哈夫曼树在编码中的应用

      哈夫曼树最早出现是为了解决电文传输最优化的问题。比如要将一段文字内容”ABDDCAA”通过网络在电文中进行传输，很自然的想法就是用二进制0和1来表示，在设计中编码过程中应该遵守两个原则：
1. 发送方传输的二进制编码，到接收方解码后必须具有唯一性，即解码结果与发送方发送的电文完全一样;
2. 发送的二进制编码尽可能地短。下面我们介绍两种编码的方式。
(1) 等长编码
      这种编码方式的特点是每个字符的编码长度相同（编码长度就是每个编码所含的二进制位数）。假设字符集只含有4个字符A，B，C，D，如下图：

      若现在有一段电文为：ABDDCAA，则应发送二进制序列：000001011011010000000，总长度为21位。当接收方接收到这段电文后，将按三位一段进行译码。这种编码的特点是译码简单且具有唯一性，但编码长度并不是最短的。

(2) 不等长编码
      在传送电文时，为了使其二进制位数尽可能地少，可以将每个字符的编码设计为不等长的，使用频度较高的字符分配一个相对比较短的编码，使用频度较低的字符分配一个比较长的编码。例如，可以为A，B，C，D四个字符分别分配0，00，01，1，并可将上述电文用二进制序列：000110100发送，其长度只有9个二进制位，但随之带来了一个问题，接收方接到这段电文后无法进行译码，因为无法断定前面3个0是3个A，1个B、2个A，即译码不唯一，这种编码方法不可使用。
      因此，为了设计长短不等的编码，以便减少电文的总长，还必须考虑编码的唯一性，即在建立不等长编码时必须使任何一个字符的编码都不是另一个字符的前缀，这宗编码称为前缀编码（prefix code）。
假设字符集4个字符A，B，C，D的频率分别为45，10, 10， 35，合起来是100%，那么，我们可以按照哈夫曼树来规划它们。如下图：

上图的构建规则为：
      （1）利用字符集中每个字符的使用频率作为权值构造一个哈夫曼树（如下图一）；
      （2）从根结点开始，为到每个叶子结点路径上的左分支赋予0，右分支赋予1，并从根到叶子方向形成该叶子结点的编码（如下图二）。
      此时A的编码为0，B的编码为100，C的编码为101，D的编码为11，对于上面的文本内容”ABDDCAA”编码的结果为”0100111110100”。当接收方接收到编码字符串时，根据上图的哈夫曼树可知，第一个0为A，第二个100为B，以此类推，从而破解成功。
      把通过哈夫曼树构建的编码称为哈夫曼编码，哈夫曼编码的关键是任意字符的编码都不是其它字符编码的前缀，保证编码的唯一性。

---

五、Java构建哈夫曼树

/**
 * @Title:哈夫曼树
 * @Description：
 * @Author： Uncle-Ming
 * @Date：2017年1月10日 下午3:16:35
 * @Version V1.0
 */
public class HuffmanTree {

    //节点数据
    static class Node {
        String data;            //数据
        double weight;  //权重
        Node left;  //左节点
        Node right; //右节点

        public Node(String data, double weight) {
            this.data = data;
            this.weight = weight;
        }

        @Override
        public String toString() {
            return "Node [data=" + data + ", weight=" + weight +  "]";
        }
    }

    /**
     * 构造哈夫曼树
     * @param nodes 节点集合
     * @return
     */
    static Node createTree(List nodes) {
        while(nodes != null && nodes.size() > 1) {
            quickSort(nodes, 0, nodes.size()-1);

            //1、获取权值最小的两个元素
            Node left = nodes.get(nodes.size()-1);
            Node right = nodes.get(nodes.size()-2);

            //2、生成新的节点
            Node node = new Node(null, left.weight + right.weight);

            //3、新节点作为两个元素的父节点
            node.left = left;
            node.right = right;

            //4、从序列中删除这两个最小的元素
            nodes.remove(left);
            nodes.remove(right);

            //5、将新元素插入到序列中
            nodes.add(node);
        }

        //最后集合中的唯一元素就是根元素
        return nodes.get(0);
    }

    /**
     * 快速排序算法（从大到小）
     * @param nodes     节点集合
     * @param start     开始位置
     * @param end       结束位置
     */
    private static void quickSort(List nodes, int start , int end) {
        if (start < end) {
            //第一个元素作为分界值
            Node base = nodes.get(start);   
            //i从左边搜索，搜索大于分界值的元素的索引  
            int i = start;  
            //j从右边开始搜索，搜索小于分界值的元素的索引  
            int j = end + 1;

            while(true) {
                //找到大于分界值的元素的索引，或i已经到了end处  
                while(i < end && nodes.get(++i).weight >= base.weight);
                //找到小于分界值的元素的索引，或j已经到了start处  
                while(j > start && nodes.get(--j).weight <= base.weight);

                if (i < j) {  
                    swap(nodes , i , j);  
                } else {
                    break;  
                }  
            }

            swap(nodes , start , j);  
            //递归排序左子序列
            quickSort(nodes , start , j - 1);
            //递归排序右边子序列  
            quickSort(nodes , j + 1, end);
        }
    }

    /**
     * 交换数组指定位置的元素
     * @param nodes 数组
     * @param i     索引值
     * @param j     索引值
     */
    private static void swap(List nodes, int i, int j) {  
        Node tmpNode = nodes.get(i);  
        nodes.set(i , nodes.get(j));  
        nodes.set(j , tmpNode);  
    }

    /**
     * 层级遍历
     * @param root
     * @return
     */
    public static List breadthFirst(Node root) {  
        Queue queue = new ArrayDeque();  
        List list = new ArrayList();  
        if(root != null) {
            //将根元素入“队列”
            queue.offer(root);
        }

        while(!queue.isEmpty()) {
            //将该队列的“队尾”的元素添加到List中  
            list.add(queue.peek());
            Node p = queue.poll();

            //如果左子节点不为null，将它加入“队列”  
            if(p.left != null) {
                queue.offer(p.left);  
            }  

            //如果右子节点不为null，将它加入“队列”  
            if(p.right != null) {
                queue.offer(p.right);
            }  
        }

        return list;  
    }  

    public static void main(String[] args) {
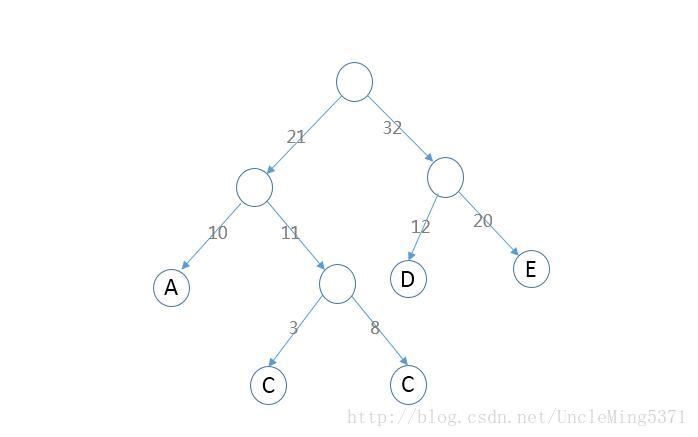
        List nodes = new ArrayList();  
        nodes.add(new Node("A" , 10));
        nodes.add(new Node("B" , 8));  
        nodes.add(new Node("C" , 3));  
        nodes.add(new Node("D" , 12));  
        nodes.add(new Node("E" , 20));  
        Node root = HuffmanTree.createTree(nodes);  
        System.out.println(breadthFirst(root));
    }
}

最终构造的哈夫曼树如下图：

---

PS：参考《大话数据结构》