2018字节跳动秋招笔试题——视频编解码岗

一、选择题

1.虚拟存储器的最大容量是由（）决定的。
A.计算机系统的地址结构和外存空间
B.页表长度
C.内存空间
D.逻辑空间

解答：AC。虚拟存储器的最大容量=min（内存+外存，2^n），n为计算机的地址总线位数。

2.进程状态相关
1）进程的特征：动态性；并发性；独立性；异步性。
2）进程的状态：

• 就绪状态：当进程已分配到除CPU以外的所有必要的资源，只要获得处理机便可立即执行，这时的状态称为就绪状态。
• 执行状态：当进程已获得处理机，其程序正在处理机上执行，此时进程的状态称为执行状态。
• 阻塞状态：正在执行的进程，由于等待某个事件发生而无法执行时，便放弃处理机而处于阻塞状态。引起进程阻塞的事件可有多种，如，等待I/O完成、申请缓冲区不能满足、等待信件（信号）等。

3）3种基本状态转换

• 就绪->执行：处于就绪状态的进程，当进程调度程序为之分配了处理机后，该进程便由就绪状态变成执行状态。
• 执行->就绪：处于执行状态的进程在其执行过程中，因为配给它的一个时间片已用完不得不让出处理机，于是进程从执行状态转为就绪状态。
• 执行->阻塞：正在执行的进程因等待某种事件发生而无法继续执行时，便从执行状态变为阻塞状态。
• 阻塞->就绪：处于阻塞状态的进程，若其等待的事件已经发生，于是进程由阻塞状态转变为就绪状态。
  参考：http://www.cnblogs.com/zyf-zhaoyafei/p/4714598.html

3.699个结点的完全二叉树，有叶子结点多少个？
A.350
B.699
C.1398
D.以上都不正确

解答：A。若设二叉树的高度为h,除第 h 层外,其它各层 (1～h-1) 的结点数都达到最大个数,第 h 层所有的节点都连续集中在最左边,这就是完全二叉树。完全二叉树是由满二叉树而引出来的。对于深度为K的,有N个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
二叉树的两个特点。1）第k层的结点个数最多为 2k−1 2 k − 1 个，高度为k层的二叉树，最多 2k−1 2 k − 1 个结点。

则在本题目敏感词699个节点,因为是完全二叉树, 210−1>699>29−1 2 10 − 1 > 699 > 2 9 − 1 ,所以高度为10,可以确定1到9层全满,节点总算为511,剩下的188个肯定为叶子节点!第10层上的188个节点挂在第九层的188/2=94个节点上,则第九层剩下的 29−1−94=162 2 9 − 1 − 94 = 162 个也为叶子节点,最后总共188+162=350个叶子节点!

4.0到9999这1万个数中有多少个数字7
解答：总共有四位数，每位数的可能分别有10种（0～9）。
每一个位，都会出现0~9的交替，实际上在出现7这个角度，各个位是一样的。
现在假设个位固定为7，那么其他的位数的变化数量是10x10x10=1000种。
就是说数字7在个位出现的次数为1000。

以此类推，数字7在十位、百位、千位出现的次数也是1000，所以答案为4x1000=4000

5.下列I/O组织方式中，主存与外设的数据交换完全是通过CPU执行程序控制完成的是（）
A.程序查询式
B.中断
C.DMA
D.通道

解答：C。
程序查询式：CPU完全介入。主机查询外设的某些状态位，若外设准备就绪，则执行一次I/O操作；若外设未准备就绪，主机将再次查询。
中断：需要CPU介入。设备控制器发出中断信号，操作系统开始逐个字节从缓冲区读入内存。在数据读入IO设备的缓冲区，发出中断前，CPU可以做其他事情。
DMA：内存和IO设备直接进行数据交换，不需要CPU干涉。但CPU在传输开始和传输结束介入。
通道：能执行有限通道指令的IO控制器，代替CPU控制外设。

6.假设一条指令的执行过程可以分为“取指令”、“分析”和“执行”三段，每一段的执行时间分别为 Δt Δ t 、 2Δt 2 Δ t 和 3Δt 3 Δ t ，顺序执行n条指令至少需要花费的时间为：
A. 3nΔt 3 n Δ t
B. 2nΔt 2 n Δ t
C. 6nΔt 6 n Δ t
D. nΔt n Δ t

解答：C
顺序执行需要的时间： T=(Δt+2Δt+3Δt)×n=6nΔt T = ( Δ t + 2 Δ t + 3 Δ t ) × n = 6 n Δ t

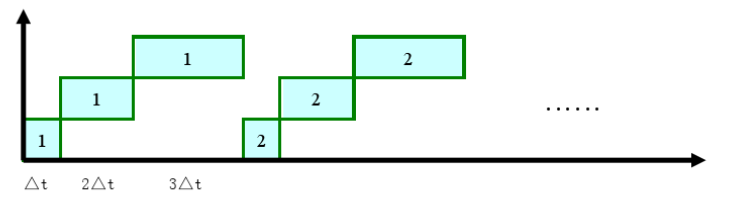
取指令和执行重叠，即一次重叠执行方式，我们假设第n+1条指令的取指令和第n条指令的执行同事结束，那么需要的时间为： T=Δt+(2Δt+3Δt)×n=5nΔt+Δt T = Δ t + ( 2 Δ t + 3 Δ t ) × n = 5 n Δ t + Δ t

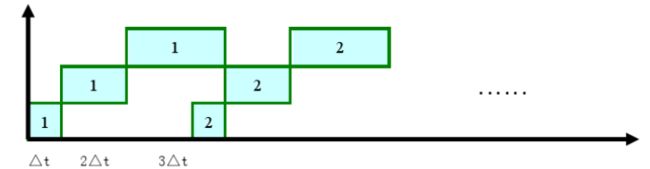
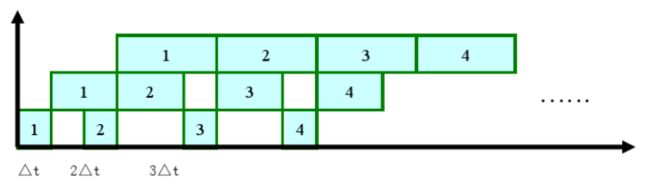
采用先行控制以后： T=Δt+2Δt+3Δt×n=3nΔt+3Δt T = Δ t + 2 Δ t + 3 Δ t × n = 3 n Δ t + 3 Δ t

7.编译过程的五个阶段
解答：

• 词法分析：输入源程序，对构成源程序的字符串进行扫描和分解，识别出一个个单词。词法分析阶段的工作中依循的是语言的词法规则（或称构词规则）。描述词法规则的有效工具是正规式和有效自动机。
• 语法分析：在词法分析的基础上，根据语言的语法规则，把单词符号串分解成各类语法单位。语法分析所依循的是语言的语法规则。语法规则通常用上下文无关文法描述。词法分析是一种线性分析，而语法分析是一种层次结构分析。
• 词义分析与中间代码产生：对语法分析所识别出的各类语法范畴，分析其含义，并进行初步翻译（产生中间代码）。这一阶段通常包括两个方面的工作。首先，对每种语法范畴进行语义安插，如，变量是否定义、类型是否正确等。如果语义正确，则进行中间代码的解释。这一阶段依循的是语言的语义规则。通常使用属性文法描述语义规则。
• 优化：对前段产生的中间代码进行加工变换，以期在最后阶段产生出更为高效的目标代码。优化的主要方面：子表达式的提取、循环优化、删除无用代码等。还可以对代码进行并行化处理。优化所依循的原则是程序的等价变换规则。
• 目标代码生成：把中间代码（或经过优化处理之后）变换成特定机器上的地基语言代码。这阶段实现了最后的翻译，它的工作有赖于硬件系统结构和机器指令含义。目标代码的形式可以是绝对指令代码或可重新定位的指令代码或汇编指令代码。如目标代码是绝对指令代码，则这种目标代码可立即执行；如目标代码是汇编指令代码，则需要汇编器汇编之后才能运行。现在多数实用编译程序所产生的目标代码都是一种可重定位的指令代码。这种目标代码在运行前必须借助于一个连接装配程序把各个目标模块（包括提醒提供的库函数）链接在一起，确定程序变量（或常数）在主存中的位置，装入内存中指定的起始地址，使之成为一个可以运行的绝对指令代码程序。

8.计算机采用分级存储体系的主要目的是为了（）
A.解决主存容量不足的问题
B.提高存储器的读写可靠性
C.提高外设访问效率
D.解决存储的容量、价格和速度之间的矛盾

解答：D。多级存储体系结构是指能达到速度、容量、成本之间的权衡，且能够应对一个通用os的需要的结构。

9.linux两个进程访问同一块共享内存，当访问的共享内存中的同一对象时，指针相同吗？
解答：不同。

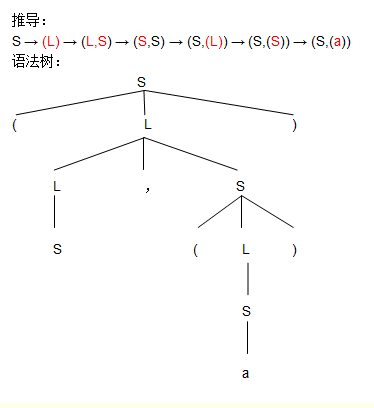
10.给定文法G=（{S,L},{a,（,）},{S→(L)|a L→L,S|S},S）.给出句型“(S,(a))”的推导和语法树.

11.甲乙两人先后掷骰子，甲先掷，先到6的为优胜，请问甲胜利的概率是多少？
解答：6/11。
获胜时，掷的点数是6，因此掷到6的概率为1/6，没有掷到6的概率为5/6。
甲获胜时，掷的次数为奇数次，因此甲获胜的概率是：
P=1/6+(5/6)2∗(1/6)+(5/6)4∗(1/6)+⋯=(1/6)[1+(5/6)2+(5/6)4+…]=(1/6)∗1/[1−(5/6)2]=6/11 P = 1 / 6 + ( 5 / 6 ) 2 ∗ ( 1 / 6 ) + ( 5 / 6 ) 4 ∗ ( 1 / 6 ) + ⋯ = ( 1 / 6 ) [ 1 + ( 5 / 6 ) 2 + ( 5 / 6 ) 4 + … ] = ( 1 / 6 ) ∗ 1 / [ 1 − ( 5 / 6 ) 2 ] = 6 / 11

12.应用层协议有哪些？
解答：
应用层/表示层：超文本传输协议HTTP、文件传输协议FTP、简单邮件传输协议SMTP、域名系统DNS、安全外壳协议SSH、动态主机配置协议DHCP、网络校时协议NTP、简单网络管理协议SNMP。
传输层：传输控制协议TCP、用户数据报文协议UDP、实时传送协议RTP、点对点隧道协议PPTP。
网络层：网际协议IP（IPv4 IPv6）、ICMP、RIP。
网络接口层：HDLC、PPP。

13.有两个从小到大排好序的数组，长度分别为N和M，将这两个数组合并成一个有序数组的最小比较次数是（）
A.Min(N,M)
B.M+N-1
C.N+M
D.Max(N,M)

解答：A。将两个数组中的元素逐个比较，小的存在中间数组里，当一个数组结束时，只需要将另外一个数组的元素复制过去即可。
最坏M+N-1。

14.若处理器有32位地址，则它的虚拟地址空间为（）字节。
A.2G
B.4G
C.100k
D.640k

解答：虚拟地址对应于物理存储空间的大小，因而可以虚拟出看起来很大的空间，这里虚拟地址的地址结构是：
31—页号—12—位移量w—0，这里的地址长度正好是操作系统的内存位数，所以可以知道最大寻址为2的32次方b，对应于kb、mb、gb的换算式如下：
2^10b=1kb
2^20b=1mb=1kb*2^10
2^30b=1gb=1mb*2^10
这里2^32=2^2*1gb=4gb

15.以太网包括哪些技术？
解答：冲突检测、载波侦听、多路访问

16.在一棵高度为5的理想平衡树中，最少含有多少个结点？
解答：高度为n，最少节点数为 2n−1 2 n − 1 个；最多节点数为 2n−1 2 n − 1
个。

17.一根木棍折断成3段构成一个三角形的概率。
解答：
设线段长度为a，任意分成三段长分别为x，y和a-x-y，显然有x>0，y>0，a-x-y>0，将这三个约束条件画到(x,y)二维平面坐标系上，这三条直线围成了一个直角三角形即为可行域（图1），其面积为(1/2)a^2。
而这三段长能构成三角形的条件是：任意两边之和大于第三边，也就是下面三个不等式得同时成立：
x + y > a - x - y (x + y < a/2)
x + a - x - y > y (y < a/2)
y + a - x - y > x (x < a/2)
我们把上面三个不等式也画在平面直角坐标系中，可以看到可行域为图2中绿色的小三角形，其面积为:(1/8)a^2 ，占整个三角形的1/4。

故此三段能构成三角形的概率为1/4。

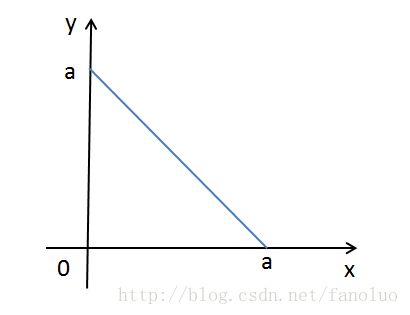
图1. 将a分成三段，每段大于零

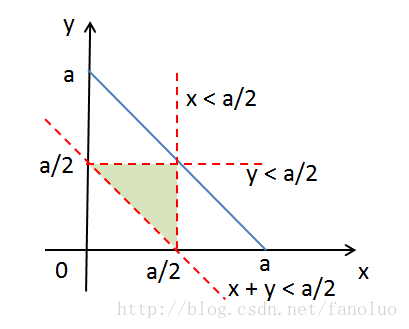
图2. 三段可以构成三角形

方法二：
我们把一根木棍看成单位1，现在要在[0, 1]区间上选两个点，使得这两点划分的三条线段可以构成三角形。

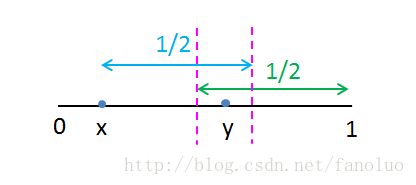
现在我们先随意放一个点，可以在[0, 1]区间上的任何点，假设位置为x（不妨设x < 1/2，在右半边是对称的情况），那么如图3所示，为了使得能够构成三角形，另外一个点可以选取的区间为图中红色虚线之间（1/2, 1/2+x）。

只考虑x在左半边的时候，可以构成三角形的概率为：

右半边是一样的1/8，因此总概率为1/4。

18.排列组合问题
https://wenku.baidu.com/view/31c4a4d73186bceb19e8bb07.html

19.IP数据包经由路由转发的时候，源IP和目的IP是否改变？
解答：不能。除非做了NAT转换才能改变，否则，数据包在整个传输过程中，源IP和目的IP不会发生改变。
不过MAC地址是变化的，因为发送端开始不知道目的主机的MAC地址，所以每经过一个路由器，MAC地址都会发生变化。（MAC Media Access Control或者Medium Access Control，媒体访问控制，或称为物理地址、硬件地址，用来定义网络设备的位置。在OSI模型中，第三层网络层负责IP地址，第二层数据链路层负责MAC地址。因此一个主机会有一个MAC地址，而每个网络位置会有一个专属于它的IP地址。MAC地址是网卡决定的，是固定的。）
http://blog.51cto.com/jettcai/1835200

20.子网掩码的计算及与子网数、主机数关系
https://blog.csdn.net/yinshitaoyuan/article/details/51782330

二、编程题

1.https://zhidao.baidu.com/question/408043611.html