数学之美~阅读

数学之美

---

目录

---

1. 统计语言模型

  假设一个有意义的句子 S 由词 w1,w2,...,wn 组成，则句子 S 出现的概率可以表示为：

P(S)=P(w1)P(w2|w1)P(w3|w2,w1)⋅⋅⋅P(wn|wn−1,wn−2,...,w1)

  从上式看出，一个词出现的概率取决于前面所有的词，然而从计算上来看，各种可能性太多，无法实现，所以可以假设一个词出现的概率只与其前一个词有关(即马尔科夫假设~ 注意，该假设为何有效？)，上式可以进行进一步得到：

P(S)=P(w1)P(w2|w1)P(w3|w2)⋅⋅⋅P(wn|wn−1)

  计算 P(wn|wn−1) 可以使用贝叶斯公式 P(wn)=P(wn,wn−1)P(wn−1) ，利用统计语言模型可以先得到在统计的文本中 (wn,wn−1)词对 出现了多少次，以及 wn−1 出现多少次，两个次数之比即可得到结果。

  统计语言模型比任何已知的借助某种规则的方法都有效！
 

贝叶斯公式： P(A|B)=P(A,B)P(B),P(A,B)=P(B|A)P(A)

---

2. 谈谈中文分词

  统计语言模型是建立在词的基础之上的，对于中日韩等语言，首先应该进行分词。如“中国航天官员应邀到美国与太空总署官员开会”。分成一穿词：中国/航天/官员/应邀/到/美国/与/太空/总署/官员/开会。
  我们可以想到的最简单的分词方式是查字典，从左到右扫描句子，碰到一个词典中有的词就标识出来，遇到复合词（如：“上海大学”）就找词匹配，遇到不认识的字串就分割成单字词。然而这种分词方法缺点是不能处理二义性的分割（如：“发展中国家”被分割成“发展-中国-家”）。
  90年代后，清华的郭进博士用统计语言模型成功解决二义性问题，将汉语分割的错误率降低一个数量级。上面一堆都是铺垫，，，重点来了，该方法用数学公式简单概括如下：
  假定句子 S 有以下几种分词方法:
  - A1,A2,A3,...,Am
  - B1,B2,B3,...,Bn
  - C1,C2,C3,...,Ck
  最好的一种方法应该保证分完词后该句子出现的概率最大，也就是说如果 A1,A2,A3,...,Am 是最好的分词方法，则

P(A1,A2,A3,...,Am)>P(B1,B2,B3,...,Bn)

P(A1,A2,A3,...,Am)>P(C1,C2,C3,...,Ck)

  （ 穷举所有可能方法并计算概率有点笨，实现技巧见注解 。）

 

实现技巧：把它看做一个动态规划问题，并利用维特比（Viterbi）算法求解

---

3. 隐马尔科夫在语言处理中的应用

  问题描述：输入信号 s1,s2,s3... （未知），输出信号 o1,o2,o3... ，（已知），我们如何通过我们的观测信号（ o1,o2,o3... ）得到输入信号（ s1,s2,s3... ）？

  我们在这里做出两个假设：

     1. 任意时刻的状态只依赖于其前一个时刻的状态，即 si 的状态只依赖于 si−1 。
     2. 任意时刻的观测只依赖于当前时刻的装填，即 oi 的状态只依赖于 si 。

  在继续之前，我们需要了解隐马尔可夫链的状态转移以及观测序列的生成过程，假设隐藏状态空间（未知的输入信号状态）包含N个状态（ s1,s2,s3,...,sN ），此时隐马尔可夫链可以形象描述为一个多段图 G （学过算法的都知道），每一层包含 N 个节点，每个节点表示状态空间中的一个状态 si ，相邻层之间的节点全连接，那么从第一层到最后一层（假设包含 T 层）的路径也就有 NT−1 条，每一条路径（记为 P ）都会包含 T 个节点，每一条路径都会以 P(o1,o2,...,oT|s1,s2,...,sT) 生成一个观测序列。
  我们此时已知变量有：多段图 G 的初始状态；节点之间的转移概率；观测序列中节点的生成概率；我们的问题是如何根据这个结构以及观测序列来得到一个最优路径（概率最大路径） P∗ ？

  我们可以使用维特比算法来得到最优路径，实质上是一个简单的动态规划问题。

 

P(o1,o2,...,oT|s1,s2,...,sT) 在语音识别中被称为”声学模型”（Acoustic Model），机器翻译中被称为”翻译模型”（Translation Model），在拼写校正中被称为”纠错模型”（Correction Model）。

---

4. 怎样度量信息?

  信息使用信息熵来量化，信息不确定性越高，信息熵越大，包含的信息越多。
  信息熵(Entropy)一般用 H 表示，单位是比特，信息熵定义如下：

P(x)=−∑XP(x)log2[P(x)]

 

---

5. 布尔代数和搜索引擎的索引

  搜索引擎对文献（每一个网页可以看做一个文献）建立索引：假设一共有 N 个文献，对于每一个关键词建立一个长度为 N 的二进制向量 v ， vi=1 表示第 i 篇文献包含该关键词。
  我们搜索时输入关键词，搜索引擎对每一个关键词的向量进行与运算，得到一个最终的向量 t ，向量中的位 ti=1 表示第i个文献包含我们输入的所有关键词。

 

由于向量包含大量的0，所以一般我们只记录为1的位即可。于是，搜索引擎的索引变成了一张大表，表的每一行代表一个关键词，每一个关键词后跟着一组数字，每一个数字表示包含该关键词的文献序号。

---

6. 图论和网络爬虫

  网络可以看做一个大图，每一个网页可以看做一个节点，每一个超链接可以看做一条边，所以网络爬虫(Web Crawlers，或被称为机器人)可以利用图的遍历算法(BFS, DFS)进行网页遍历。
  网络爬虫可以从一个门户网站出发，下载网页，并且寻找该网页中的超链接，然后进入每一个超链接持续这一过程。为了避免下载同一个页面，我们可以对每一个下载的页面使用哈希表(HashTable)进行标记。
 

---

7. 信息论在信息处理中的应用

  互信息是对两个随机事件相关性的度量，比如随机事件北京今天下雨和随机变量空气湿度的相关性很大，但是和随机事件你明天表白成功是相关性几乎无关，互信息就是用来量化度量这种相关性的。

  可以解决机器翻译中的二义性问题，对于每一个含义我们可以得到与其一起出现的互信息最大的一些词，从而确定含义的时候可以看一下哪类相关的词多。

  相对熵用来衡量两个正函数是否相似，对于两个相同的函数，它们的相对熵为0。也可以用来描述两个概率分布 P 和 Q 差异。

  在自然语言处理中，相对熵可以用来描述两个常用词(语法和语义)是否同义，或者两篇文章是否相近。我们可以利用相对熵得到信息检索中一个重要的概念：词频率-逆向文档频率(TF/IDF)

 

  互信息定义：设两个随机变量 (X,Y) 的联合分布为 p(x,y) ，边际分布分别为 p(x),p(y) ，互信息I(X;Y)表示为：

I(X;Y)=∑x∈X∑y∈Yp(x,y)logp(x,y)p(x)p(y)

   交叉熵定义(KL散度)：设 P(x),Q(x) 是X取值的两个离散概率分布，则P对Q的相对熵表示为：

D(P||Q)=∑P(x)logP(x)Q(x)

---

8. 贾里尼克的故事和现代语言处理

  贾里尼克很牛叉 !
 

---

9. 如何确定网页和查询的相关性

  给定查询词 w1,w2,...,wN ，我们直觉是选择出现查询词出现最多的网页，但是我们会发现，网页越长，出现查询词的个数可能越多，所以我们对每一个网页中的查询词进行归一化，即查询词数量/网页中词的总数量，表示为TF(term frequency)，我们可以得到每一个网页中查询词出现的频率 TF1,TF2,...,TFN ，计算词的出现频率 TF=TF1+TF2+...+TFN ，最终我们优先推荐查询词出现频率最高的网页。
  以”原子能 的 应用”为例，”的”一般在所有中文网页中都会有出现，而”应用”也是一个通用词汇，我们从不同的词中获取的信息量不一样，所以我们应该对每一个词加上一个权重，记包含词 wi 的文档个数为 Di ，一般 Di 越大，我们给的权重应该越低。
  在信息检索中，我们多定义逆文本频率指数IDF来表示权重( logD/Dw ， D 表示文本总数， Dw 表示出现查询词的文档个数)，我们得到相关性计算公式：

R=TF1∗IDF1+TF2∗IDF2+...+TFN∗IDFN

 

  IDF概念就是一个特定条件下，关键词概率分布的交叉熵。
  到目前为止了解了如何自动下载网页，如何建立索引，如何衡量网页质量(PageRank)，如何确定网页和查询的相关性，我们应该可以写一个简单的搜索引擎。

---

10. 有限状态机和地址识别

  使用有限状态机(FSM)进行地址识别，根据我们的输入，什么省，什么市，什么区，什么街道，如果输入的地址可以从FSM的起始状态跳转到终止状态，说明该地址应该有效。
  我们需要解决两个问题，如何使用有效的地址建立FSM？如何根据FSM进行地址字串的匹配？这两个问题的解决都有现成的算法。
  基于FSM进行地址匹配的方法在实际应用中有局限性，只能进行精准匹配，如果输入错误或者不符合规范就会束手无策，所以我们想要进行模糊匹配，为达到这一目的，产生了基于概率的有限状态机，这种基于概率的FSM和离散的马尔科夫链基本等效。

 

---

11. Google的阿卡47制造者阿米特.辛格博士

  简单就是美！
 

---

12. 余弦定理和新闻分类

  对两篇新闻 a,b ，我们一个想法是将两篇新闻表示成两个N维向量 X,Y ( X∈RN,Y∈RN )，然后使用余弦定理计算两则新闻在该N维空间的夹角( cos(X,Y) )，将该值作为两篇新闻的相似度。
  现在的问题是如何将新闻转换成N维实值向量：对字典(实词个数为N)中的每一个实词，计算其在一篇新闻中的单文本TF/IDF(见9)，没有出现的词值为0，最终可以得到代表该新闻的向量( X=[x1,x2,...,xN] ， xi 表示第i个实词在该文档中的TF/IDF值)。
 

---

13. 信息指纹及其应用

  任何一段文字都可以对应一个不太长的随机数，随机数的存储比文字存储更节省存储空间，由于该随机数本身代表了该段文字信息，可被称为信息指纹，以在网络爬虫防止重复下载同一页面。
  信息指纹的关键技术是伪随机数产生算法，对不同的信息可以产生不同的伪随机数，可以用于信息安全领域。
 

---

14. 谈谈数学模型的重要性

1. 一个正确的数学模型应该在形式上是简单的。
2. 大量准确的数据对研发很重要。
3. 正确的模型很可能受到噪声干扰，而显得不准确；这时，我们不应该使用一种凑合的方法来弥补它，而是要找到噪声的根源，这也许能通往重大发现。

---

15. 繁与简 自然语言处理的几位精英

  柯林斯：追求完美
  布莱尔：简单就是美

---

16. 不要把所有的鸡蛋放到一个篮子里 最大熵模型

  在自然语言处理中，我们经常会遇到各种各样但又不完全确定的信息，我们需要使用一个统一的模型把这些信息综合到一起。怎么综合信息是一门大学问！
  举个栗子，在拼音转化汉语中，我们输入wang-xiao-bo，那这是王小波还是王晓波？我们不知道，但是我们知道如果文章主题是文学相关，是前者的概率大一些，如果是讨论两岸关系的话，是后者的概率大一些。在该例子中，我们只需要综合两类不同信息：主题信息和上下文信息。
  数学上最漂亮的方法是最大熵模型：当我们需要对一个随机事件的概率分布进行预测时，我们的预测应该满足全部已知条件，而对未知的情况不要做任何主观假设。说白了就是保留全部不确定性，将风险降到最小。
  最高香农奖得主希萨(Csiszar)证明，对任何一组不自相矛盾的信息，这个最大熵模型不仅存在而且唯一。它们都有一个非常简单的形式——指数函数。
  以下是根据上下文(前两个词 w1,w2 )和主题预测( subject )下一个词( w3 )的最大熵模型：

P(w3|w2,w1,subject)=eλ1(w1,w2,w3)+λ2(subject,w3)Z(w1,w2,subject)

 

  最大熵模型在形式上是最漂亮的统计模型，而在实现上是最复杂的模型之一。
  决定股票涨落的因素有几十甚至上百种，而最大熵方法恰恰能找到一个同时满足成千上万中不同条件的模型。所以可以利用最大熵模型和一些数学工具进行股票预测。

---

18. 矩阵运算和文本处理中的分类问题

  自然语言处理中，最常见的两类分类问题是文本按主题归类；词汇表中的字词按意思归类。
  对文本的分类一般有两种方法，第一种是计算文本之间的相关性：首先将文本转化为一个实值向量(实词向量，相当于特征提取过程)，然后相关性可以使用两个文本实值向量的夹角表示。但是，如果文本数量太大，如一百万篇文章，两两比较需要比较五千亿次，计算量太大，不可行。第二种是奇异值分解(SVD)：用矩阵 A 表示文章和词的关联性：

A=⎡⎣⎢⎢⎢⎢⎢⎢a11...ai1...aM1.........a1jaijaMj.........a1N...aiN...aMN⎤⎦⎥⎥⎥⎥⎥⎥

  在矩阵 A 中，每一行表示一篇文章，每一列表示一个实词，对矩阵 A 分解：

A=XBY

  其中： X∈RM∗K,B∈RK∗K,Y∈RK∗N 。
   其中 X 中的每一行表示意思相关的一类词，其中每一个非零元素表示这类词中每个词的重要性(或者相关性)，数值越大越相关。 Y 每一列表示同一主题一类文章，其中每个元素表示这类文章中每篇文章相关性。 B 表示类词和文章之间的相关性。因此一次矩阵分解同时完成了近义词分类和文章分类，以及每类文章和每类词之间的相关性。

现在已经有SVD的并行计算方法。

---

19. 马尔科夫链的扩展 贝叶斯网络

  现实世界中，很多事物的相互联系不能简单使用一条链串起来(类似隐马尔可夫链)，所以隐马尔可夫链(HMM)只是对现实世界的一种粗略描述，对事物之间错综复杂的联系更合理的方法是使用有向图表示，每一个节点表示一个状态，每一条边表示状态之间的转移概率（因果关系），网络中每一个节点的概率计算可以使用贝叶斯公式，因此叫做贝叶斯网络，由于转移概率是一种量化的可信度，所以贝叶斯网络也被称为信念网络(belief networks)。
  使用贝叶斯网络必须知道各个状态之间的转移概率，得到这些参数需要利用一些已知数据进行训练。相比HMM，贝叶斯网络的训练理论上是一个NP-complete问题，也就是说对于现在的计算机是不可计算的，但是对于某些应用，这个训练过程可以简化，并在计算上实现。
 

  贝叶斯网络在图像处理，文字处理，支持决策等方面有很多应用。在文字处理方面，语义相近的词之间的关系可以用一个贝叶斯网络来描述。我们利用贝叶斯网络可以找到近义词和相关的词，在Google搜索和Google广告中都有直接应用。

---

21. 布隆过滤器

  布隆过滤器(Bloom Filter)用于判断一个元素是否属于一个集合，在网络爬虫中可以判断一个网页是否下载过，或者在垃圾邮件处理中判断一个邮件地址是否是垃圾邮件地址。
  以后者为例，如果我们需要存储一亿个邮件地址，我们先建立一个16亿的二进制向量 v ，并将所有位清零。存储一个电子邮件地址：使用八个随机数产生器 F1,F2,...,F8 对该地址处理产生八个信息指纹 f1,f2,...,f8 ，然后用一个随机数产生器 G 将八个信息指纹 f1 ~ f8 映射到八个0-16亿之间的整数 g1,g2,...,g8 ，将二进制向量v中 g1 ~ g8 对应的位置1。如果要判断一个电子邮件是否是垃圾邮件，可以对该邮件进行相同的处理，如果对应的八个位全部是1则说明该邮件为垃圾邮件(误识概率很低)。
 

---

22. 谈谈密码学的数学原理

  密码学应用的数学知识很简单。

---

23. 输入一个汉字需要敲多少个键 谈香农第一定律

  由香农第一定理我们可以知道汉字编码长度的最小值是汉字的信息熵。
  假设每一个汉字频率 p1,p2,...,pN ，它们的编码长度分别为 L1,L2,...,LN ，那么平均编码长度为：

L¯¯¯=p1L1+p2L2+...+pNLN

---

24. 从全球导航到输入法–谈动态规划

  全球导航有两个关键技术：卫星定位；根据用户输入的起点和终点确定最短路线；每个城市可以看做一个节点，城市之间的通路可以看做一条边。如我们可以利用该导航确定从北京到广州的最短路线会经过哪些城市。
  如果城市数量较多，那么枚举所有的路线绝对是个笨方法，那我们怎么做呢？
  我们在中国地图中间切一刀得到线 l1 ：

  那么我们可以计算从北京到这条线上的所有城市的最短距离，然后将该线往南推移得到 l2 ，北京到线 l2 上所有城市的最短路径都必然包含北京到线 l1 上的城市，以此类推，最终得到一个类似多段图（学过算法的都知道）的一个抽象图，从而可以使用动态规划来解该多段图。

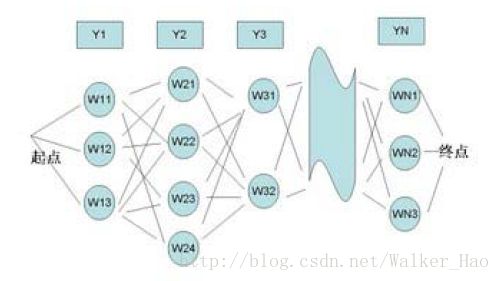
  在输入法中，我们可以将汉语输入看做一个通信问题，而输入法则是将拼音串到汉字串的转换器，如图所示：

   Y1,Y2,...,YN 是用户输入的拼音串，而 w11,w12,w13 是第一个拼音 Y1 对应的候选汉字，同理 w21,w22,w23,w24 是第二个拼音 Y2 对应的候选汉字。从第一个字到最后一个字可以组成很多句子，我们的输入法就是根据上下文找到一个最优的句子。(是不是像多段图里的最短路径问题？)如果我们将上下文的相关性量化，作为从前一个汉字到后一个汉字的距离，那么寻找输入拼音下最合理的句子就变成了一个典型的最短路径问题，可以使用动态规划求解。
 

---

参考

  吴军《数学之美》