《BP神经网络的MATLAB实现》
-
- 一 BP神经网络实现不使用MATLAB神经网络工具箱
- 问题
- 分析
- MATLAB实现代码
- 运行结果
- 绘制的图像
- 二 使用MATLAB的神经网络工具箱简易实现BP网络
- 问题
- 分析
- 工具箱中的相关函数一些参考了MATLAB自带的英文手册
- mapminmax函数
- newff函数新版本
- 关于nettrainParam的常用属性
- train函数
- sim函数
- MATLAB实现代码
- 运行结果
- 绘制的图像
- 一 BP神经网络实现不使用MATLAB神经网络工具箱
一. BP神经网络实现(不使用MATLAB神经网络工具箱)
1. 问题
公路运量主要包括公路客运量和公路货运量两方面。某个地区的公路运量主要与该地区的人数、机动车数量和公路面积有关,已知该地区20年(1990-2009)的公路运量相关数据如下:
人数/万人
20.55 22.44 25.37 27.13 29.45 30.10 30.96 34.06 36.42 38.09 39.13 39.99 41.93 44.59 47.30 52.89 55.73 56.76 59.17 60.63
机动车数量/万辆
0.6 0.75 0.85 0.9 1.05 1.35 1.45 1.6 1.7 1.85 2.15 2.2 2.25 2.35 2.5 2.6 2.7 2.85 2.95 3.1
公路面积/单位:万平方公里
0.09 0.11 0.11 0.14 0.20 0.23 0.23 0.32 0.32 0.34 0.36 0.36 0.38 0.49 0.56 0.59 0.59 0.67 0.69 0.79
公路客运量/万人
5126 6217 7730 9145 10460 11387 12353 15750 18304 19836 21024 19490 20433 22598 25107 33442 36836 40548 42927 43462
公路货运量/万吨
1237 1379 1385 1399 1663 1714 1834 4322 8132 8936 11099 11203 10524 11115 13320 16762 18673 20724 20803 21804
2. 分析
样本数据较多,且已知影响数据的因素(三大因素:该地区的人数、机动车数量和公路面积),可考虑将其作为BP神经网络的训练集,对该神经网络进行训练,然后对训练好的神经网络进行测试,最后使用测试合格的神经网络进行预测工作。
3. MATLAB实现代码
BP_road.m
numberOfSample = 20; %输入样本数量
%取测试样本数量等于输入(训练集)样本数量,因为输入样本(训练集)容量较少,否则一般必须用新鲜数据进行测试
numberOfTestSample = 20;
numberOfForcastSample = 2;
numberOfHiddenNeure = 8;
inputDimension = 3;
outputDimension = 2;
%准备好训练集
%人数(单位:万人)
numberOfPeople=[20.55 22.44 25.37 27.13 29.45 30.10 30.96 34.06 36.42 38.09 39.13 39.99 41.93 44.59 47.30 52.89 55.73 56.76 59.17 60.63];
%机动车数(单位:万辆)
numberOfAutomobile=[0.6 0.75 0.85 0.9 1.05 1.35 1.45 1.6 1.7 1.85 2.15 2.2 2.25 2.35 2.5 2.6 2.7 2.85 2.95 3.1];
%公路面积(单位:万平方公里)
roadArea=[0.09 0.11 0.11 0.14 0.20 0.23 0.23 0.32 0.32 0.34 0.36 0.36 0.38 0.49 0.56 0.59 0.59 0.67 0.69 0.79];
%公路客运量(单位:万人)
passengerVolume = [5126 6217 7730 9145 10460 11387 12353 15750 18304 19836 21024 19490 20433 22598 25107 33442 36836 40548 42927 43462];
%公路货运量(单位:万吨)
freightVolume = [1237 1379 1385 1399 1663 1714 1834 4322 8132 8936 11099 11203 10524 11115 13320 16762 18673 20724 20803 21804];
%由系统时钟种子产生随机数
rand('state', sum(100*clock));
%输入数据矩阵
input = [numberOfPeople; numberOfAutomobile; roadArea];
%目标(输出)数据矩阵
output = [passengerVolume; freightVolume];
%对训练集中的输入数据矩阵和目标数据矩阵进行归一化处理
[sampleInput, minp, maxp, tmp, mint, maxt] = premnmx(input, output);
%噪声强度
noiseIntensity = 0.01;
%利用正态分布产生噪声
noise = noiseIntensity * randn(outputDimension, numberOfSample);
%给样本输出矩阵tmp添加噪声,防止网络过度拟合
sampleOutput = tmp + noise;
%取测试样本输入(输出)与输入样本相同,因为输入样本(训练集)容量较少,否则一般必须用新鲜数据进行测试
testSampleInput = sampleInput;
testSampleOutput = sampleOutput;
%最大训练次数
maxEpochs = 50000;
%网络的学习速率
learningRate = 0.035;
%训练网络所要达到的目标误差
error0 = 0.65*10^(-3);
%初始化输入层与隐含层之间的权值
W1 = 0.5 * rand(numberOfHiddenNeure, inputDimension) - 0.1;
%初始化输入层与隐含层之间的阈值
B1 = 0.5 * rand(numberOfHiddenNeure, 1) - 0.1;
%初始化输出层与隐含层之间的权值
W2 = 0.5 * rand(outputDimension, numberOfHiddenNeure) - 0.1;
%初始化输出层与隐含层之间的阈值
B2 = 0.5 * rand(outputDimension, 1) - 0.1;
%保存能量函数(误差平方和)的历史记录
errorHistory = [];
for i = 1:maxEpochs
%隐含层输出
hiddenOutput = logsig(W1 * sampleInput + repmat(B1, 1, numberOfSample));
%输出层输出
networkOutput = W2 * hiddenOutput + repmat(B2, 1, numberOfSample);
%实际输出与网络输出之差
error = sampleOutput - networkOutput;
%计算能量函数(误差平方和)
E = sumsqr(error);
errorHistory = [errorHistory E];
if E < error0
break;
end
%以下依据能量函数的负梯度下降原理对权值和阈值进行调整
delta2 = error;
delta1 = W2' * delta2.*hiddenOutput.*(1 - hiddenOutput);
dW2 = delta2 * hiddenOutput';
dB2 = delta2 * ones(numberOfSample, 1);
dW1 = delta1 * sampleInput';
dB1 = delta1 * ones(numberOfSample, 1);
W2 = W2 + learningRate * dW2;
B2 = B2 + learningRate * dB2;
W1 = W1 + learningRate * dW1;
B1 = B1 + learningRate * dB1;
end
%下面对已经训练好的网络进行(仿真)测试
%对测试样本进行处理
testHiddenOutput = logsig(W1 * testSampleInput + repmat(B1, 1, numberOfTestSample));
testNetworkOutput = W2 * testHiddenOutput + repmat(B2, 1, numberOfTestSample);
%还原网络输出层的结果(反归一化)
a = postmnmx(testNetworkOutput, mint, maxt);
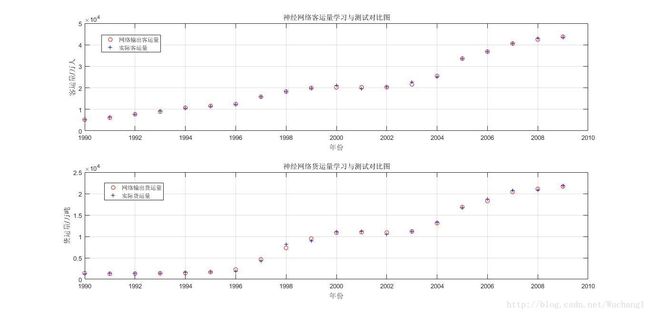
%绘制测试样本神经网络输出和实际样本输出的对比图(figure(1))--------------------------------------
t = 1990:2009;
%测试样本网络输出客运量
a1 = a(1,:);
%测试样本网络输出货运量
a2 = a(2,:);
figure(1);
subplot(2, 1, 1); plot(t, a1, 'ro', t, passengerVolume, 'b+');
legend('网络输出客运量', '实际客运量');
xlabel('年份'); ylabel('客运量/万人');
title('神经网络客运量学习与测试对比图');
grid on;
subplot(2, 1, 2); plot(t, a2, 'ro', t, freightVolume, 'b+');
legend('网络输出货运量', '实际货运量');
xlabel('年份'); ylabel('货运量/万吨');
title('神经网络货运量学习与测试对比图');
grid on;
%使用训练好的神经网络对新输入数据进行预测
%新输入数据(2010年和2011年的相关数据)
newInput = [73.39 75.55; 3.9635 4.0975; 0.9880 1.0268];
%利用原始输入数据(训练集的输入数据)的归一化参数对新输入数据进行归一化
newInput = tramnmx(newInput, minp, maxp);
newHiddenOutput = logsig(W1 * newInput + repmat(B1, 1, numberOfForcastSample));
newOutput = W2 * newHiddenOutput + repmat(B2, 1, numberOfForcastSample);
newOutput = postmnmx(newOutput, mint, maxt);
disp('预测2010和2011年的公路客运量分别为(单位:万人):');
newOutput(1,:)
disp('预测2010和2011年的公路货运量分别为(单位:万吨):');
newOutput(2,:)
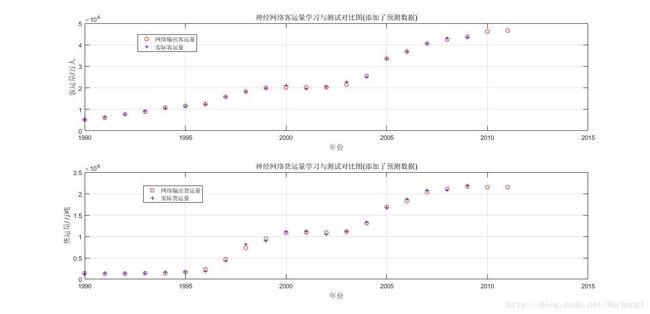
%在figure(1)的基础上绘制2010和2011年的预测情况-------------------------------------------------
figure(2);
t1 = 1990:2011;
subplot(2, 1, 1); plot(t1, [a1 newOutput(1,:)], 'ro', t, passengerVolume, 'b+');
legend('网络输出客运量', '实际客运量');
xlabel('年份'); ylabel('客运量/万人');
title('神经网络客运量学习与测试对比图(添加了预测数据)');
grid on;
subplot(2, 1, 2); plot(t1, [a2 newOutput(2,:)], 'ro', t, freightVolume, 'b+');
legend('网络输出货运量', '实际货运量');
xlabel('年份'); ylabel('货运量/万吨');
title('神经网络货运量学习与测试对比图(添加了预测数据)');
grid on;
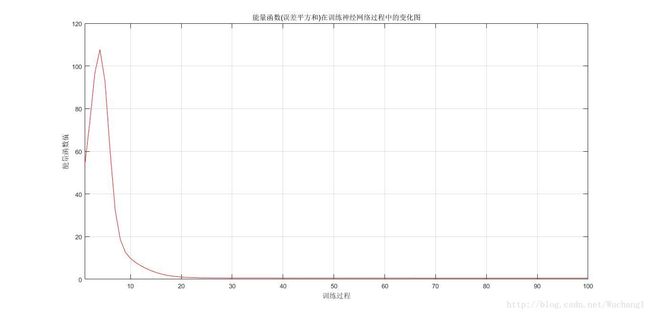
%观察能量函数(误差平方和)在训练神经网络过程中的变化情况------------------------------------------
figure(3);
n = length(errorHistory);
t3 = 1:n;
plot(t3, errorHistory, 'r-');
%为了更加清楚地观察出能量函数值的变化情况,这里我只绘制前100次的训练情况
xlim([1 100]);
xlabel('训练过程');
ylabel('能量函数值');
title('能量函数(误差平方和)在训练神经网络过程中的变化图');
grid on;4. 运行结果
预测2010和2011年的公路客运量分别为(单位:万人):
ans =
1.0e+04 *
4.6188 4.6601
预测2010和2011年的公路货运量分别为(单位:万吨):
ans =
1.0e+04 *
2.1521 2.1519
5. 绘制的图像
可以看出,使用BP网络中的负梯度下降原理之后,效果显著。
二. 使用MATLAB的神经网络工具箱简易实现BP网络
1. 问题
同<一>
2. 分析
同<一>
3. 工具箱中的相关函数(一些参考了MATLAB自带的英文手册)
mapminmax函数
- 功能:通过将原矩阵每行的最小值和最大值映射到[YMIN,YMAX]来得到规范化的矩阵。
- 算法:y = ( ymax - ymin ) * ( x - xmin ) / ( xmax - xmin ) + ymin
(注:当xmax与xmin相等时,则对原矩阵使用mapminmax函数仍得到原矩阵)
- 默认算法:
(默认情况下,mapminmax函数的YMIN和YMAX分别是-1和1)
y = 2 * ( x - xmin ) / ( xmax - xmin ) - 1
[Y,PS] = mapminmax(X)
- X:原矩阵
- Y:对矩阵X进行规范化得到的矩阵
- PS:存放关于原矩阵规范化过程中的相关映射数据的结构体
[Y,PS] = mapminmax(X,FP)
X:原矩阵
FP:含有字段FP.ymin和FP.ymax的结构体
Y:对矩阵X进行规范化得到的矩阵(使用在FP的ymin和ymax规定下的算法)
PS:存放关于原矩阵规范化过程中的相关映射数据的结构体
Y = mapminmax(‘apply’,X,PS)
- ’apply’:必写
- X:原矩阵
- PS:存放关于某个矩阵规范化过程中的相关映射数据的结构体
- Y:对矩阵X进行规范化得到的矩阵(使用PS中的规范化方式)
X = mapminmax(‘reverse’,Y,PS)
- ’reverse’:必写
- Y:某个矩阵
- PS:存放关于某个矩阵规范化过程中的相关映射数据的结构体
- X:将矩阵Y反规范化得到的矩阵(使用PS中的规范化方式,这里指将矩阵X转换为矩阵Y的规范化方式)
newff函数(新版本)
a. 功能:建立一个前馈反向传播(BP)网络。
b. net=newff(P,T,S)
- P: 输入数据矩阵。(RxQ1),其中Q1代表R元的输入向量。其数据意义是矩阵P有Q1列,每一列都是一个样本,而每个样本有R个属性(特征)。一般矩阵P需要事先归一化好,即P的每一行都归一化到[0 1]或者[-1 1]。
- T:目标数据矩阵。(SNxQ2),其中Q2代表SN元的目标向量。数据意义参考上面,矩阵T也是事先归一化好的。
- S:第i层的神经元个数。(新版本中可以省略输出层的神经元个数不写,因为输出层的神经元个数已经取决于T)
c. net = newff(P,T,S,TF,BTF,BLF,PF,IPF,OPF,DDF)(提供了可选择的参数)
- TF:相关层的传递函数,默认隐含层使用tansig函数,输出层使用purelin函数。
- BTF:BP神经网络学习训练函数,默认值为trainlm函数。
- BLF:权重学习函数,默认值为learngdm。
- PF:性能函数,默认值为mse。
- PF,OPF,DDF均为默认值即可。
d. 常用的传递函数:
- purelin:线性传递函数
- tansig:正切 S 型传递函数
- logsig: 对数 S 型传递函数
(注意:隐含层和输出层函数的选择对BP神经网络预测精度有较大影响,一般隐含层节点传递函数选用tansig函数或logsig函数,输出层节点转移函数选用tansig函数或purelin函数。)
关于net.trainParam的常用属性
(假定已经定义了一个BP网络net)
* net.trainParam.show: 两次显示之间的训练次数
* net.trainParam.epochs: 最大训练次数
* net.trainParam.lr: 网络的学习速率
* net.trainParam.goal: 训练网络所要达到的目标误差
* net.trainParam.time: 最长训练时间(秒)
train函数
功能:训练一个神经网络
[NET2,TR] = train(NET1,X,T)(也可[NET2] = train(NET1,X,T) )
- NET1:待训练的网络
- X: 输入数据矩阵(已归一化)
- T:目标数据矩阵(已归一化)
- NET2:训练得到的网络TR:存放有关训练过程的数据的结构体
sim函数
功能:模拟Simulink模型
SimOut = sim(‘MODEL’, PARAMETERS)
- (见名知意,不必再解释)
4. MATLAB实现代码
BP_toolbox_road.m
%准备好训练集
%人数(单位:万人)
numberOfPeople=[20.55 22.44 25.37 27.13 29.45 30.10 30.96 34.06 36.42 38.09 39.13 39.99 41.93 44.59 47.30 52.89 55.73 56.76 59.17 60.63];
%机动车数(单位:万辆)
numberOfAutomobile=[0.6 0.75 0.85 0.9 1.05 1.35 1.45 1.6 1.7 1.85 2.15 2.2 2.25 2.35 2.5 2.6 2.7 2.85 2.95 3.1];
%公路面积(单位:万平方公里)
roadArea=[0.09 0.11 0.11 0.14 0.20 0.23 0.23 0.32 0.32 0.34 0.36 0.36 0.38 0.49 0.56 0.59 0.59 0.67 0.69 0.79];
%公路客运量(单位:万人)
passengerVolume = [5126 6217 7730 9145 10460 11387 12353 15750 18304 19836 21024 19490 20433 22598 25107 33442 36836 40548 42927 43462];
%公路货运量(单位:万吨)
freightVolume = [1237 1379 1385 1399 1663 1714 1834 4322 8132 8936 11099 11203 10524 11115 13320 16762 18673 20724 20803 21804];
%输入数据矩阵
p = [numberOfPeople; numberOfAutomobile; roadArea];
%目标(输出)数据矩阵
t = [passengerVolume; freightVolume];
%对训练集中的输入数据矩阵和目标数据矩阵进行归一化处理
[pn, inputStr] = mapminmax(p);
[tn, outputStr] = mapminmax(t);
%建立BP神经网络
net = newff(pn, tn, [3 7 2], {'purelin', 'logsig', 'purelin'});
%每10轮回显示一次结果
net.trainParam.show = 10;
%最大训练次数
net.trainParam.epochs = 5000;
%网络的学习速率
net.trainParam.lr = 0.05;
%训练网络所要达到的目标误差
net.trainParam.goal = 0.65 * 10^(-3);
%网络误差如果连续6次迭代都没变化,则matlab会默认终止训练。为了让程序继续运行,用以下命令取消这条设置
net.divideFcn = '';
%开始训练网络
net = train(net, pn, tn);
%使用训练好的网络,基于训练集的数据对BP网络进行仿真得到网络输出结果
%(因为输入样本(训练集)容量较少,否则一般必须用新鲜数据进行仿真测试)
answer = sim(net, pn);
%反归一化
answer1 = mapminmax('reverse', answer, outputStr);
%绘制测试样本神经网络输出和实际样本输出的对比图(figure(1))-------------------------------------------
t = 1990:2009;
%测试样本网络输出客运量
a1 = answer1(1,:);
%测试样本网络输出货运量
a2 = answer1(2,:);
figure(1);
subplot(2, 1, 1); plot(t, a1, 'ro', t, passengerVolume, 'b+');
legend('网络输出客运量', '实际客运量');
xlabel('年份'); ylabel('客运量/万人');
title('神经网络客运量学习与测试对比图');
grid on;
subplot(2, 1, 2); plot(t, a2, 'ro', t, freightVolume, 'b+');
legend('网络输出货运量', '实际货运量');
xlabel('年份'); ylabel('货运量/万吨');
title('神经网络货运量学习与测试对比图');
grid on;
%使用训练好的神经网络对新输入数据进行预测
%新输入数据(2010年和2011年的相关数据)
newInput = [73.39 75.55; 3.9635 4.0975; 0.9880 1.0268];
%利用原始输入数据(训练集的输入数据)的归一化参数对新输入数据进行归一化
newInput = mapminmax('apply', newInput, inputStr);
%进行仿真
newOutput = sim(net, newInput);
%反归一化
newOutput = mapminmax('reverse',newOutput, outputStr);
disp('预测2010和2011年的公路客运量分别为(单位:万人):');
newOutput(1,:)
disp('预测2010和2011年的公路货运量分别为(单位:万吨):');
newOutput(2,:)
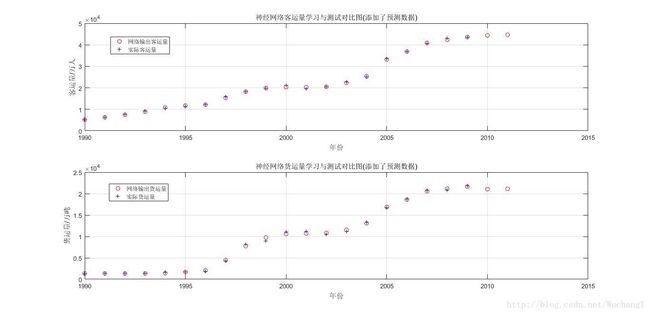
%在figure(1)的基础上绘制2010和2011年的预测情况-------------------------------------------------------
figure(2);
t1 = 1990:2011;
subplot(2, 1, 1); plot(t1, [a1 newOutput(1,:)], 'ro', t, passengerVolume, 'b+');
legend('网络输出客运量', '实际客运量');
xlabel('年份'); ylabel('客运量/万人');
title('神经网络客运量学习与测试对比图(添加了预测数据)');
grid on;
subplot(2, 1, 2); plot(t1, [a2 newOutput(2,:)], 'ro', t, freightVolume, 'b+');
legend('网络输出货运量', '实际货运量');
xlabel('年份'); ylabel('货运量/万吨');
title('神经网络货运量学习与测试对比图(添加了预测数据)');
grid on;5. 运行结果
预测2010和2011年的公路客运量分别为(单位:万人):
ans =
1.0e+04 *
4.4384 4.4656
预测2010和2011年的公路货运量分别为(单位:万吨):
ans =
1.0e+04 *
2.1042 2.1139