矩阵求最短路径
题目:
给定一个M×N的矩阵,定义一条路径为:从矩阵左上顶点数字出发到达右下数字,每一次只可以从一个数字出发向右移动一步或向下移动一步,定义路径和为:路径经过的数字的和。要求编写一个程序,找到路径和最小的那条路径,并给出最小路径和。
给定如图所示矩阵:一条路径为2->0->3->6->9->5,路径和为25
[2 ,0 ,11,1 ]
[4 ,3 ,6 ,12]
[7 ,10,9 ,5 ]
要求:测试时输入一个矩阵(输入方式随意),然后程序输出该矩阵的最小路径和与路径。
思路:动态规划求解。dp[i][j]表示从点D[0][0]到点D[i][j]的最短路径和。
对于点D[i][j]它只能从点D[i-1][j]或者点D[i][j-1]而来,所以有递推公式dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + D[i][j]; 特殊的,对于第一行的点D[0][j]只可能由点D[0][j-1]而来;对于第一列的点D[i][0]只可能由点D[i-1][0]而来。
代码解答:
#include
using namespace std;
const int maxn = 1001; //行列最大值
int M,N,K=0; //M行N列,路径有K个结点
int D[maxn][maxn]; //存储原始矩阵值
int dp[maxn][maxn]; //从D[0][0]到D[i][j]路径最小值
int mp[maxn]; //保存路径中的结点值
int main(){
cin >> M >> N;
for(int i=0; i
for(int j=0; j
cin >> D[i][j];
dp[0][0]=D[0][0];
for(int i=1; i
dp[i][0] = dp[i-1][0]+ D[i][0]; //对于第一列的点D[i][0],只可能是从上面的点D[i-1][0]往下走
for(int j=1; j
dp[0][j] = dp[0][j-1]+ D[0][j]; //对于第一行的点D[0][j],只可能是从左边的点D[0][j-1]往右走
for(int i=1; i
for(int j=1; j
dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + D[i][j];
int i=M-1,j=N-1;
mp[K++]=D[i][j];
while(i>=0 && j>=0){ //倒着找路径上的点
if(i==0 && j==0){
break;
} else if(i==0){ //在第一行上,那么上一个点只能是左边的点
mp[K++]=D[i][j-1];
j--;
} else if(j==0){ //在第一列上,那么上一个点只能是上面的点
mp[K++]=D[i-1][j];
i--;
} else { //否则就找左边和上面的dp最小对应的那个点D
if(dp[i-1][j]
mp[K++]=D[i-1][j];
i--;
} else {
mp[K++]=D[i][j-1];
j--;
}
}
}
for(int i=K-1;i>=0;i--){
cout<
if(i!=0) cout<<"->";
}
cout << endl << dp[M-1][N-1] <
return 0;
}
//测试
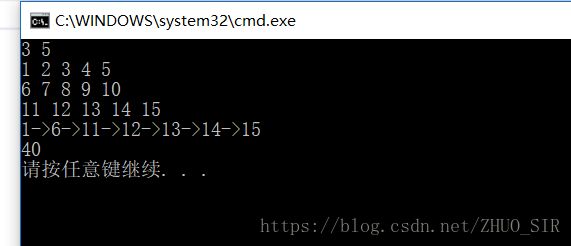
结果如下图: