C++ 之 STL
一、STL简介
是标准的模板库,将常见的数据结构以及算法进行封装。
特点:1.通用+灵活
2.效率
二、六大部件
1.容器:
1)vector(动态顺序表):底层维护了一端连续的空间
2)string(字符的动态顺序表)
3)list(双向循环链表)
list的迭代器不可以使用原生态指针。底层不是一段连续的空间。
要将原生态的指针进行封装。因此需要将一些指针多具有的操作在类中进行重载。
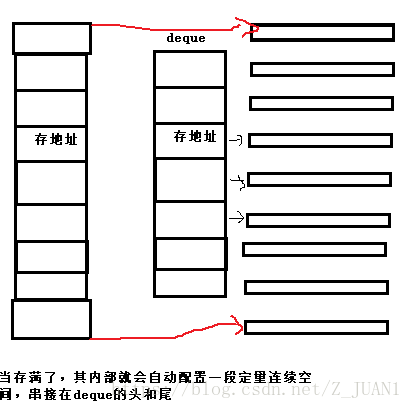
4)deque(双向开口的假想连续空间)
deque实则是维护一些分段定量的连续空间,将这些分段连续的空间管理好,造成其连续空间的假想,用户在使用时是一段连续的空间
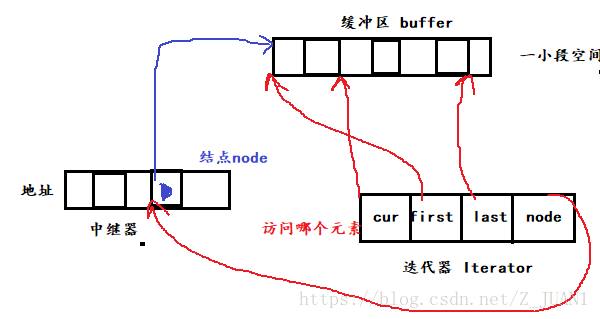
这是迭代器,缓冲区,中继器之间的相互关系。
5)适配器
stack(先进后出)(尾插尾删)-->vector,但由于增容代价大,采用deque,增容效率高,不用拷贝,直接再给一段空间。
queue(先进先出)(头删尾插)-->list,用 deque ,不涉及遍历,用deque比较方便
priority——queue(堆) 默认为大堆
关联式容器:
一、里面存放的是具有关联关系的键值对
键值实际是结构体:pair :first,second
二、二叉搜索树
1.左子树也是二叉搜索树,右子树也是二叉搜索树
2.左子树最左侧的为最小值,右子树最右侧为最大值。
3.中序是有序的
查找效率:log(N)
但是对于搜索二叉树来说,极端情况下会成为单支,退化成链表查找效率:O(N)
因此:底层并没有选择二叉搜索树,而是对此进行了优化。
三、AVL
搜索二叉树中每个结点的左右子树高度差(平衡因子)绝对值不超过1
平衡因子绝对值>1,就要进行旋转处理。
插入过程:
1.按照二叉搜索树的规则插入新节点
2.更新平衡因子
四、红黑树
但是对于AVL,删除的时候可能要一直旋转到根,效率太低。因此采用一种近似平衡的二插搜索树---->红黑树
:保证最长路径不超过最短路径的两倍。
性质:
1.每个结点不是红色就是黑色
2.根节点是黑色--->每次结点插入,就将根设为黑色
3.如果一个节点是红色,那么他的两个孩子都为黑色--->永远没有连在一起的红色
4.对于每一个接待,从该结点到其所有后代的简单路径上,均包含相同数目的
黑色结点个数---->默认插入颜色为红色-->可能违反性质3-->在调整
5.每个叶子结点都为黑色(空节点)--->为了保证第2点
插入过程:
1.按照二叉搜索树的规则插入新节点
2.检测数是否违反规则
为什么红黑树可以保证最长路径是最短路径的两倍
极端情况(不可能存在的),每两个黑色结点之间插入红色
五、底层为红黑树的关联式容器:
1.map(
2.multimap(
3.set(值
4.multiset:(值
operator[]:底层用的insert实现的,为什么不用find?
是因为find去找。找到了返回数据,找不到就无法返回。
对于insert。insert(make.pair(x.T())).first.scond
1)若存在返回与之对应的值
2)不存在。insert就会构造一个默认的值,插入到红黑树中。返回这个默认值。若为内置类型,这个值可能为空。
也就是说用insert不管你要数据存不存在都会返回。
底层为哈希的关联式容器:无序
unorder_map
unorder_multimap
unorder_set
unorder_multiset
map和undered_map的区别?
1.map有序 undered_map无序
2.底层结构不一样 (1)红黑树(2)哈希桶
3.查找效率 (1)O(logn) (2) O(1)
4.插入的方式:(1)按照搜索二叉树的规则插入新节点,在调整
(2)通过哈希函数计算桶号,插入节点 可能会产生哈希冲突
5. 应用场景:(1)如果需要有序的关联式容器--->map
(2) 与是否有序无关--->查找效率高--->underedmap
6.空间利用率:O(N)--->map(用一个插一个)
underedmap-->如果哈希冲突-->概率较高-->徐散列-->增加桶的个数
7.迭代器
map--->双向的
undered_map--->单向的--->单链表
迭代器什么时候会失效?
指针指向的空间不能访问
每个容器负责给出相应的迭代器-->容器知道自己是哪种数据结构
vector:(1)如果有扩容的操作-->迭代器会失效--->需要重新赋值
(resize,reserve,insert,push_back)
删除不会出错,空间不会释放,但会变得没有意义。(删的是最后一个。如果删的是中间,就会进行数据搬移,还是有意义的)
list (2)删除结点会失效,已经free了
插入不会
仿函数:又叫函数对象,一种行为类似函数的对象。调用者可以向函数一样使用用该对象。
实现:用户只需要实现一种新的类型,在类中进行重载(),参数根据用户索要进行的操作选择匹配
template
class Greater
{
public:
bool operator()(const T& left,const T& right)
{
return left > right;
}
};
template
void BubbleSort(T* array,size_t size,Com Compare)
{
bool isChange = false;
for (size_t i = 0; i < size - 1; ++i)
{
isChange = false;
for (size_t j = 0; j < size - 1 - i; ++j)
{
if (Compare(array[j + 1], array[j])) //compare是对象,去调用了函数
{
swap(array[j], array[j + 1]);
isChange = true;
}
}
if (!isChange)
return;
}
}
void test()
{
int array[] = { 2, 1, 5, 4, 6, 8, 9, 0, 3 };
BubbleSort(array, 9, Greater());
}