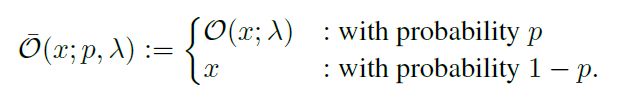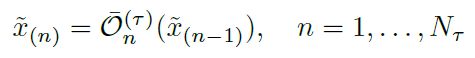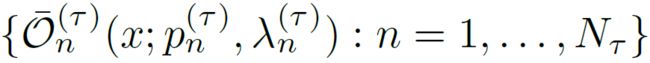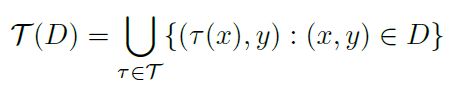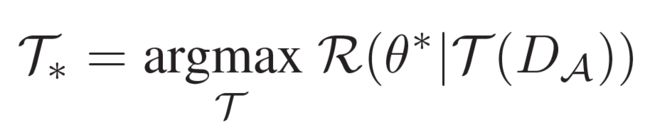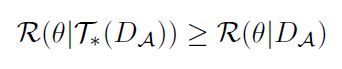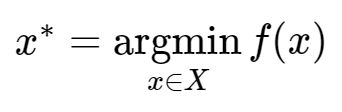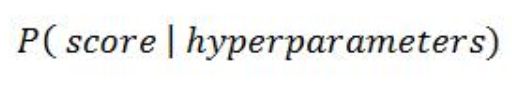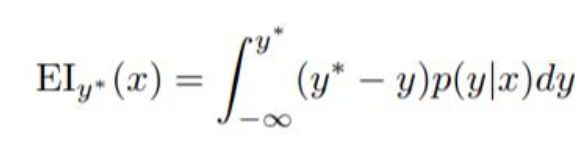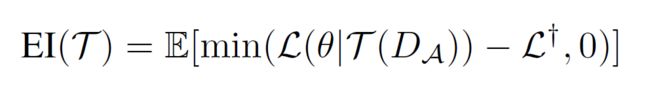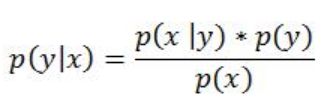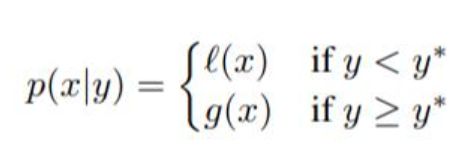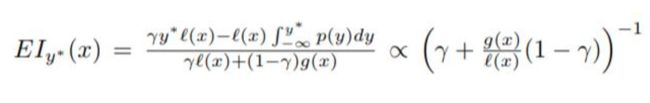Fast AutoAugment论文解读

写在前面

第一次完整地读完一篇英文论文，上来就搞得那么硬核其实我也不想……（毕竟要做Paper Reading汇报）

本文所写仅为自己的理解（只求理解，所以可能会缺乏专业性……），可能有不少错漏之处，此外现在对贝叶斯优化那块还不是太清楚……如有错误请各位大佬指出，感激不尽~

 

背景

数据增强是一种较为常用的可提高模型性能的技术，通过对数据集中的图片进行旋转、对称、颜色变换等操作，提升数据集中图片的数量及多样性，进而在训练后提高模型的泛化能力。传统数据增强方法是学者通过专业知识手动设计增强方案。如今，谷歌推出的AutoAugment使用增强学习算法，对于给定数据集，可让机器学习其特征，自动进行数据增强。

AutoAugment虽然实现了“AutoAugment”且在不少图像识别任务中达到了SOTA性能，但其训练速度实在是太慢。而在此之后出现的Fast AutoAugment（也就是本文的主角）提出了比前者快得多的自动数据增强的算法。

 

算法细节

增强策略

首先提增强策略，Fast AutoAugment与AutoAugment类似，每个增强策略有多个子策略组成，每个子策略又由多个图像增强操作组成（如剪切、旋转等等），每个操作还有两个参数：概率p，幅度λ。概率指有多大的概率执行该操作，幅度指如果执行操作，执行的幅度为多少（例如某操作是旋转，对应的幅度越大，旋转角也就越大，当然不是所有的操作都要有幅度，比如翻转），我们用O表示操作，x表示输入的图像数据，有：

因为对于某个操作是有一定概率不执行的，不执行的话输出图像与输入一致，所以对于单个操作，可用执行后的输出图像和概率p来表示。因此，可用这种递推的形式来表示有Nτ个操作并按一定顺序执行的某个子策略τ：

  表示经第i次操作后输出的图像。边界条件：

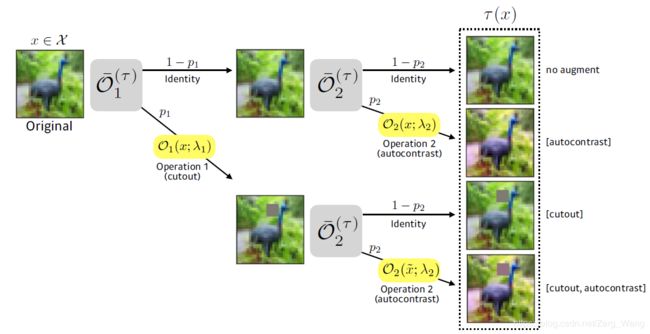
当然也可以用集合的形式表示子策略τ：

这里再提一点Fast AutoAugment与AutoAugment不一样的地方。一方面是AutoAugment的每个子策略规定由两个操作构成，而Fast对此没有要求；另一方面是AutoAugment的操作中概率p和幅度λ是离散取值，例如p的只能取0.1、0.2、0.3……但Fast为连续取值，相比离散的搜索空间就有更多的取值可能。

这里放一张原论文的图像，展示了一个由两个操作组成的子策略：

这里要提一下图中运用的一个操作“Cutout”：对于输入图像，随机选取其中的一块方形区域进行屏蔽（抹除）。

我们最终的目标，是要找到一个由个子策略组成的策略：

D为数据集，x，y分别为图像和对应的标签。

密度匹配（Density Matching）

论文提出使用密度匹配算法来寻找最佳增强策略。假设我们用于算法的分类模型为M，模型中的相关参数统称为θ。对于给定的数据集D及模型M，我们有期望准确度（expected accuracy）：

以及期望损失（expected loss）：

接下来论文提出了如何评估增强策略的好坏，具体做法为：将数据集分成和，其中用于学习模型参数θ，用于搜索增强策略。对此，我们希望找到的应该满足：

理想的（即），应该是在经过其增强后的上，模型能取得最高准确度，由前文可知，是在上训练出来的，然而在经过增强后的上还能取得最高的准确度，说明该策略是行之有效的。在保持模型参数不变的情况下，模型在和增强后的上均取得最好性能，说明该增强策略使得这两个数据集尽可能地”密度匹配“了。

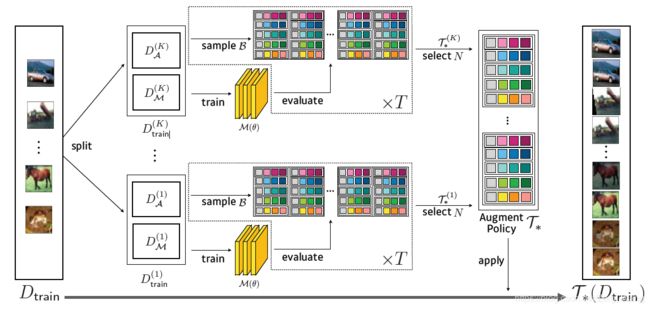
上图源自原论文，可以看出，算法不会仅在一份与上寻找最佳增强策略，类似于K折交叉验证法，在一开始会将训练数据集分成K份，逐份寻找，之后对于找到的B个增强策略（称为”候选策略“），我们选择其中最好的N个加入到我们的最佳策略列表中。最终，我们要实现：

贝叶斯优化（Bayesian Optimization）

密度匹配算法给予了我们对策略的评判标准，现在要通过贝叶斯优化来寻找这B个候选策略。首先简单讲讲贝叶斯优化的思想。

贝叶斯优化常用于超参数搜索中，假设X=x1,x2,...,xn为一组超参数的集合，又假设要优化的损失函数（目标函数）为f(X)，则我们的目的是找到这样的X：

显然，对于各种各样的超参数的数值组合，一个个代入模型计算f(X)进而比较超参数优劣的做法并不现实，这种做法在每一次取超参数的值并代入计算时与之前的任一次取值没有任何关系，换句话说，它并没有学习到之前的”失败经验“。

贝叶斯优化会跟踪过去的评估结果，并使用这些结果形成概率模型，将超参数映射到目标函数的得分概率：

这个概率函数又被称为目标函数的“代理”。一般也可写为p（y | x），可以理解为：在使用超参数x的前提下，要达到分数y的概率。

一般代理会比目标函数更容易优化，因此该方法会通过选择在代理函数上表现最佳的超参数来更新迭代。具体步骤为：

1. 建立目标函数的“代理”概率模型
2. 找到在代理上表现最佳的超参数
3. 将这些超参数应用于真正的目标函数
4. 更新包含新结果的代理模型
5. 重复步骤2-4，直到达到设定的迭代次数

这个过程也可简单概括为：我们形成了一个任务的初始视图（称为先验），然后在任务的尝试中根据新经验更新我们的模型（更新的模型称为后验）。在这里，我们的先验是y服从高维正态分布，因此随着实验（迭代）次数的增多，这个正态分布的“轮廓”也就更清楚，也就越能通过其来找到使y更好的x。

有鉴于此，在选择新的超参数进行优化迭代的时候，我们可以借鉴之前的经验，然而，这个所谓的“借鉴”过程又该如何实现？

通过当前所知的正态分布的轮廓，我们可以选择获得一个较好的x，这个选择叫做“Exploitation”，即“利用”。然而这个x可能只是个局部最优值，如果把有限的迭代次数都使用在找这些局部最优值，显得过于“目光短浅”。

此外还可选择一个之前未探索过的x，其对应的y可能并不好，但更多的“失败经验”也就能将这个正态分布的“轮廓”勾勒地更清楚，更有助于寻找到全局最优的x。这叫“Exploration”，即“探索”。

显然，极端偏向“探索”还是“利用”都是不对的，而我们寻找全局最优的x也就是一个“探索—利用”结合的过程，即Exploration-Exploitation。

而选择函数（Acquisition Function）则平衡了“探索”与“利用”，这个函数规定了从代理函数中选择下一组超参数的标准。常用的有预期改进（Expected Improvement，EI）、POI(probability of improvement)等，这里仅介绍EI：

这里y*是目标函数的阈值（一般取目前所得的最小y值），y是使用超参数x所得的目标函数值。我们希望y越小越好，因此y*-y可视为“得分”，因此整个函数可视为y*-y在(-∞, y*]的期望，若选择函数EI的值为正，说明取x得到的y要比y*更好，因此能使EI尽可能大的x即为我们所求。

论文给出的选择函数：

相比起来这个EI函数就更为简洁，其中后面这个长得像与上面提到的y*类似。我们的最终目标，是要找到使目标函数尽可能小的。

通过以上这些根据“先验”来寻找更佳超参数的方式，避免了对于大量超参数组合反复计算f(x)的情况，从而达到极高的算法效率。

Tree-structured Parzen Estimator （TPE）

论文中所用的贝叶斯优化中，还使用了TPE进一步优化。

在上面的EI函数中现身的p(y|x)在TPE中使用贝叶斯公式替换为p(x|y)：

对于p(x|y)，即在目标函数值为y下取超参数x的概率，为什么p(x|y)会有多个值呢，这是因为在贝叶斯优化中，代理函数是逐步迭代更新的，因此在不同时期代理函数即使输入相同，输出也不一定相同。

然后随着一系列变换，可将EI函数变形为：

以下为原论文给出的伪代码：

注意这里输入的T，我理解为“步数”或“迭代次数”，和前面所提的策略不一样……

 

效果展示及一些结论

与AutoAugment对比

为了直观、公平地与AutoAugment对比，Fast AutoAugment将超参数设置地尽可能与AutoAugment一致，对于一些难以与AutoAugment相较的超参数，Fast 则将其设置为与Baseline一致。论文中提到的Fast的超参数设置有：

数据集份数K=5，搜索宽度T=2，搜索深度（候选策略数）B=200，选定的策略N=10。

效果分析

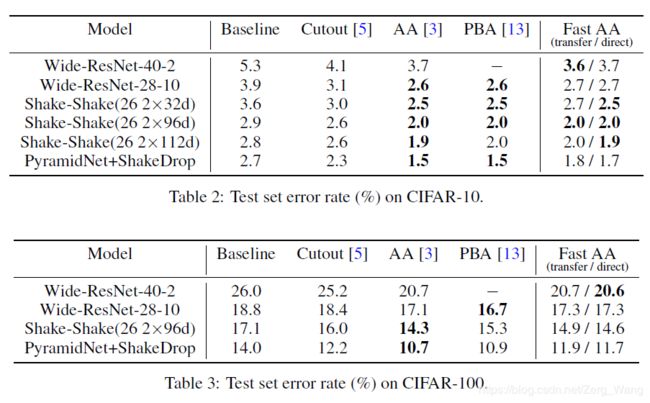
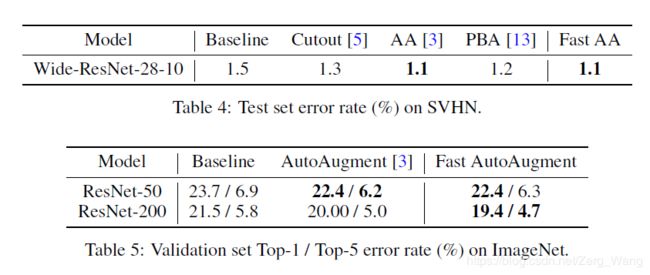
可以看出无论在PBA还是AutoAugment面前，Fast AutoAugment在准确度上还是不遑多让的，然而最重要的一点是，Fast要比前面的那些算法快太多了：

这里值得一提的是，AutoAugment训练所用的为Tesla P100显卡，而Fast用的是Tesla V100。虽然V100的计算性能要比P100强上不少，但这上千倍的速度提升还是足以说明Fast AutoAugment的确在速度上有巨大优势。

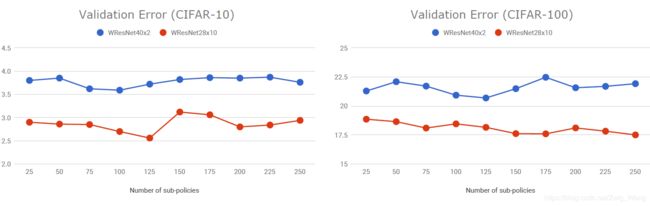
训练中提高子策略对准确度的影响

当子策略在100~125以内时，随着子策略数量的提高，模型的准确度也随之提高。

直接训练与策略迁移间准确度不同的原因

搜索增强策略所用的模型和拿增强数据集再训练的模型可能不一致，这些差距一定程度上可以表面Fast AutoAugment算法得出的增强策略是否具有迁移性。通过上面的表格可以看出，随着模型越大，直接训练和策略迁移所得的准确度之差也会越大，因为在小模型上搜索出的增强策略对提高大模型的泛化能力还是有局限性的。

更改贝叶斯优化中的参数

论文中说可以这样做，但按他们的经验来说，可能对提高模型表现没什么用……

 

参考资料

https://arxiv.org/pdf/1905.00397v2.pdf

https://github.com/kakaobrain/fast-autoaugment

http://imgtec.eetrend.com/blog/2019/100018057.html

https://www.cnblogs.com/marsggbo/p/9866764.html