LDA主题模型学习心得

LDA主题模型

LDA 简介

LDA模型：Latent Dirichlet Allocation是Blei 等人于2003年提出的基于概率模型的主题模型算法，它是一种非监督机器学习技术，可以用来识别大规模文档集或预料库中的潜在隐藏的主题信息。
LDA算法的核心思想：每篇文章由多个主题mix混合而成的，而每个主题可以由多个词的概率表征。该方法假设每个词是由背后的一个潜在隐藏的主题中抽取的。
而对于每篇文档：
1.对于每篇文档，从主题分布中抽取一个主题。
2.从上述抽到的主题所对应的单词分布中抽取一个单词。
3.重复上述过程直至遍历文档中的每个单词。

---

---

LDA 算法的输入

算法输入：分词后的文章集、主题数K、超参数 α 和 β
算法输出：
1.每篇文章的各个词被指定的主题编号:tassign-model.txt
2.每篇文章的主题概率分布 θ :theta-model.txt
3.每个主题下的词概率分布 ϕ :phi-model.txt
4.程序中词语word的id映射表：wordmap.txt
5.每个主题下 ϕ 概率排序从高到低top n特征词：twords.txt

必备的数学知识

Gamma函数

gamma函数其实就是阶乘的函数，比如n!=1*2*3*….n,这个阶乘形式可以更一般化，不局限于整数。而更一般的函数形式就是gamma函数：

Γ(x)=∫+∞0e−ttx−1dt(x>0)

Γ(1)=∫+∞0e−tdt=−[e−t]+∞0=1 , Γ(12)=π‾‾√ , Γ(x+1)=xΓ(x) , Γ(n)=(n−1)!
有兴趣可以证明一下，感觉复杂的记住就可以了。

二项分布（Binomial distribution）

二项分布即重复n次独立的伯努利实验。每次实验的结果只能是1或者0，每次实验相互独立，当实验次数为1时，就是伯努利分布，每次为1的概率都是相等的。
二项分布的概率公式：

P=Cknpk(1−p)n−k

其中p为成功的概率，记作X~B(n,p)

beta分布（beta distribution）

beta分布是指一组定义在区间(0,1)的连续概率分布，有两个参数 α 和 β ,且 α , β >0.它是一个作为伯努利分布与二项分布的共轭先验分布的密度函数。
例：空气中的相对湿度可能符合beta分布（主要帮助大家理解）. 相对湿度即现在的含水量与空气中的最大含水量（饱和含水量）的比值，显然该值只能出现于0-1之间。空气中出现某个相对湿度具有随机性。
Beta分布的概率密度函数：

f(x;α,β)=1B(α,β)xα−1(1−x)β−1

记作X~ Beta( α,β ),其中分母函数为B函数。 （注意不是二项分布）
B函数与Gamma函数的关系：
B（ α,β ）= Γ(α)Γ(β)Γ(α+β)
Beta分布的期望可以用 αα+β 来估计。
以上结论有兴趣可以证明一下，感觉复杂的记住就可以了。

多项分布（multinomial distribution）

多项分布是二项分布的推广，在n次独立试验中每次只输出k种结果中的一个，且每种结果都有一个确定的概率p.
举例来说，投掷n 次骰子，这个骰子共有6种结果输出，骰子1点出现的概率为 p1 ,2点出现的概率为 p2 ，…理论上出现的概率是相等的，但是也可以不想等，只要各个输出结果出现的事件互斥且概率和为1即可。同时统计各个点数出现的次数，这个结果组合的事件就应该服从多项分布。
多项分布的概率函数：

f(x1,...,xk;n,p1,...pk)=Γ(∑ixi+1)∏iΓ(xi+1)∏i=1kpxii

狄利克雷分布（dirichlet distribution）

狄利克雷分布是beta分布在多项情况下的推广，也是多项分布的共轭先验分布。
二项分布和多项分布很相似，beta分布与狄利克雷分布很相似，beta分布是二项式分布的共轭先验概率分布，而狄利克雷分布是多项分布的共轭先验概率分布。
那么，问题来了，什么是共轭先验分布？

共轭先验分布（conjugacy prior）

共轭，就是我们选取一个函数作为似然函数(likelihood function)的prior probability distribution，使得后验分布函数（posterior distributions）和先验分布函数形势一致。其中涉及到贝叶斯估计。根据贝叶斯规则，后验分布＝似然函数＊先验分布，分布可以作为下一次计算的先验分布，如果形式相同，就可以形成一个链条，为了使先验分布与后验分布的形式相同，那么就称先验分布与似然函数是共轭的，即共轭指的是先验分布与似然函数。
简单的理解：用二项分布的共轭先验概率分布来说，先验分布X~Beta( α,β )变成了X~beta( α+s,β+f ), 如果有新增的观测值，那么该后验分布又可以作为先验分布乘以似然函数来计算。得到修正后的新后验分布，如果新旧分布的形式一致，那么就可以看作是共轭的。大致就是这个意思。

LDA的Gibbs Sampling推导

unigram假设

unigram假设其实简单的理解就是词袋模型
文档的生成可以用投骰子来模拟：
骰子有V个面，每个面代表一个词，每个面的概率是 p⃗ =(p1,p2,...,pv) ，投掷N次骰子每个面产生的次数分别是 n⃗ =(n1,n2,...,nv) 次，然后计算生成语料库的概率。
引入Dirichlet分布作为多项分布的先验分布，即文本单词概率 p⃗  ~ Dir(p⃗ |α⃗ ) ，加入Dirichlet分布后，我们不知道骰子的样式（具体有多少个面），所以从一个服从Dirichlet分布的瓶子中抽取一个骰子，然后投掷生成文档。
通过参数估计：每个单词产生的概率估计值是对应事件的先验的伪计数和数据中的计数的和在整体计数中的比例。

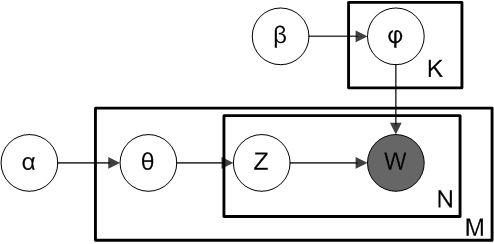
Latent Dirichlet ALLocation Intro

M代表训练语料中的文章数；
K代表设置的主题数；
V代表训练语料库中出现的所有词的词表；
θ 是一个M*K的矩阵， θ⃗ m 代表第m篇文章的主体分布；
ϕ 是一个K*V的矩阵， ϕ⃗ k 代表编号为k的主题之上的词分布；
α 是每篇文档的主题分布的先验分布Dirichlet分布的参数（超参数），其中 θ⃗ i ~ Dir(α⃗ ) ;
β 是每个主题的词分布的先验分布Dirichlet分布的参数（超参数），其中 ϕk ~ Dir(β⃗ ) ;
W是可被观测的词；

---

对于每篇文档，LDA的生成过程：
1.选择 θ⃗ i ~ Dir(α⃗ ) ;(i=1,2,…,M)
2.选择 ϕk ~ Dir(β⃗ ) ;(k=1,2,…,K)
3.对于每个单词位置 Wi,j (j=1,…, Ni ),(i=1,…,M)
4.选择一个topic主题服从 zi,j ~ Multinomial(θi)
5.选择一个word词服从 wi,j ~ Multinomial(ϕzi,j)

---

简单的理解：
i.从服从 θm→ ~ Dir(α⃗ ) 的箱子中抽取一个文档–主题骰子，重复一下过程
ii.投掷这个doc-topic骰子，得到一个topic编号z
iii.从服从 ϕk ~ Dir(β⃗ ) 分布的箱子里共有主题–单词骰子中选择编号为z的那个，投掷这个骰子，于是得到一个词。
总结：先抽取一个doc-topic骰子 θm→ ,投掷生成第n个词的主题词编号 zm.n ，在K个topic-word骰子 ϕk→ 中，挑选编号为k= zm,n 的那个骰子投掷，然后生成word: wm,n ,生成语料中第m篇文档的第n个词。

马尔可夫链

马尔可夫链就是根据一个转移概率矩阵去转移的随机过程（马尔可夫过程）。在已知目前的状态（现在）的条件下，它未来的演变不依赖于它以往的演变（过去）。
马尔可夫过程中会形成一个转移矩阵，位置向量在若干次转移后会达到一个稳定的状态。这个状态称之为平稳分布状态。若要达到这个状态需要满足两个性质:1.马尔可夫链的所有状态节点需要可以彼此通信，不能有割裂的孤岛。2.非周期性，链条不会再特定的周期内在两个节点来回循环。

采样公式:Collapsed Gibbs Sampling采样

整个文本训练集生成的联合概率：

p(w⃗ ,z⃗ |α⃗ ,β⃗ )=p(w⃗ |z⃗ ,β⃗ )p(z⃗ |α⃗ )

总结

在LDA迭代过程中，不断的对每个单词的topic编号重新指定， θ⃗ (doc−>topic) 和 ϕ⃗ (topic−>word) 两个概率向量是迭代训练完成通过期望公式计算的。
训练验证模型质量的好坏，可以使用perplexity公式：

bH(q)=b−1N∑Ni=1logbq(xi)

perplexity的值越小，说明模型越好。