【笔记】HMM在股票指数中的简单应用

简述

这里要感谢一位研究生师兄分享了我这篇文章
https://www.ricequant.com/community/topic/788/
本文，是对上面文章的梳理，并做出了在本地条件下使用的代码

过程

隐藏马尔可夫（HMM）过程本质上，根据显式的数据，反推隐藏的状态。
类似于从输出链反推导出状态链。而每个状态，都有对应的输出可能。
这里假设所有的特征向量都服从高斯分布。（这个假设是自然的。中心极限定理，大数定理了解一下~）

关于实现这份代码中，遇到了很多坑。

• pandas.Series.multiply()含义解释
• pandas.DataFrame.multiply()含义解释
• 【解决办法】read_csv()第一列作为index
• DeprecationWarning: Function log_multivariate_normal_density is deprecated; The function log_multiva
• 如何下载沪深300历史数据
• 考虑到jupyter上的连续性操作，和普通的Python脚本之间的不同，所以，我们需要调用np.argsort()来得到最优的几个判断因子。

代码

• 环境：Python 3.6 + Windows10
• 调用的所有库都需要pip install
• 所调用的数据包文件名为 1.csv。下载方式为上面链接中的最后一个的，第二种下载方式。

from hmmlearn import hmm
import numpy as np
from matplotlib import pyplot as plt
import pandas as pd
n = 6  # 6个隐藏状态

data = pd.read_csv('1.csv', index_col=0)
volume = data['volume']
close = data['close']

logDel = np.log(np.array(data['high'])) - np.log(np.array(data['low']))
logRet_1 = np.array(np.diff(np.log(close)))
logRet_5 = np.log(np.array(close[5:])) - np.log(np.array(close[:-5]))
logVol_5 = np.log(np.array(volume[5:])) - np.log(np.array(volume[:-5]))

# 保持所有的数据长度相同
logDel = logDel[5:]
logRet_1 = logRet_1[4:]
close = close[5:]

Date = pd.to_datetime(data.index[5:])
A = np.column_stack([logDel, logRet_5, logVol_5])

model = hmm.GaussianHMM(n_components=n, covariance_type="full", n_iter=2000).fit(A)
hidden_states = model.predict(A)

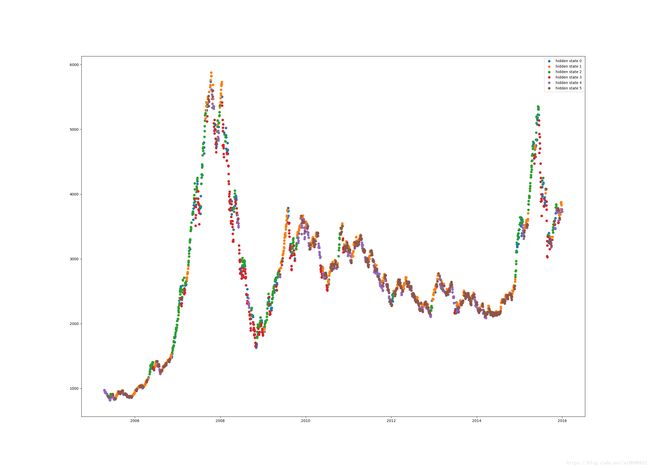
plt.figure(figsize=(25, 18))
for i in range(n):
    pos = (hidden_states == i)
    plt.plot_date(Date[pos], close[pos], 'o', label='hidden state %d' % i, lw=2)
    plt.legend()
plt.show()

res = pd.DataFrame({'Date': Date, 'logReg_1': logRet_1, 'state': hidden_states}).set_index('Date')
series = res.logReg_1

templist = []
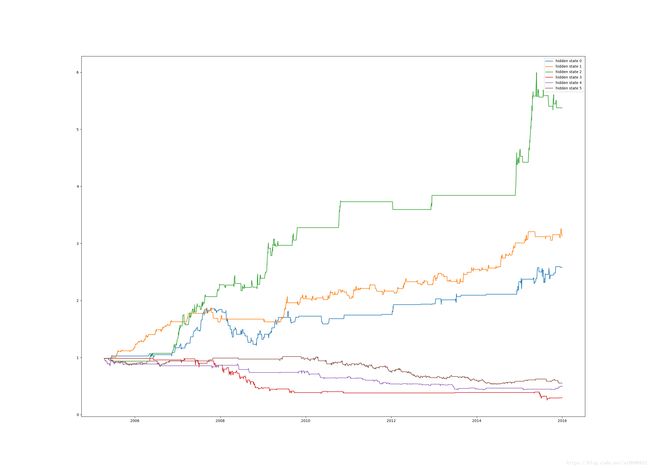
plt.figure(figsize=(25, 18))
for i in range(n):
    pos = (hidden_states == i)
    pos = np.append(1, pos[:-1])
    res['state_ret%d' % i] = series.multiply(pos)
    data_i = np.exp(res['state_ret%d' % i].cumsum())
    templist.append(data_i[-1])
    plt.plot_date(Date, data_i, '-', label='hidden state %d' % i)
    plt.legend()
plt.show()

templist = np.array(templist).argsort()
long = (hidden_states == templist[-1]) + (hidden_states == templist[-2])  # 买入
short = (hidden_states == templist[0]) + (hidden_states == templist[1])  # 卖出
long = np.append(0, long[:-1])
short = np.append(0, short[:-1])

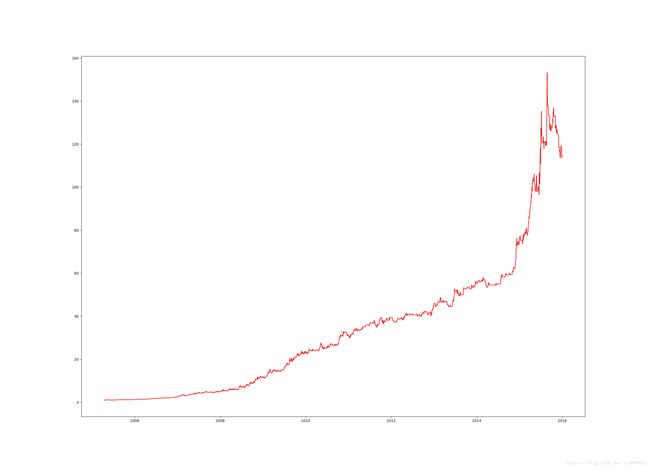
plt.figure(figsize=(25, 18))
res['ret'] = series.multiply(long) - series.multiply(short)
plt.plot_date(Date, np.exp(res['ret'].cumsum()), 'r-')
plt.show()

数据图

实用性分析

• 由于采用多因子最后整合的出来的效果，所以，对于交易的时候乘上的那个数值可能是大于1的数（这方面的考量上，这里最多是2，最小是0）
• 对于每个因子，以及后期的交易上，都是采用每日收盘价的收益率（即今天的收盘价减去昨天的收盘价）求和之后，再e^x函数外包一下。这里，我不是很确定跟采用复利的情况下的区别。不过两者的增幅上都是同一量级的。
• 最后算整个的情况的时候，是先将整个模型分为买入和卖出两个部分分别计算之后，再做收益率的求和变化。但实际交易过程中肯定是不可能这么简单的分的。
• 还有，这里假设了估计是想要钱就来钱的模型。比如说，这里有可能出现，需要做买入某个指数，和卖出某个指数的操作，当然，做期货交易的时候，都是需要提交一定的佣金的。这里没有考虑这个问题。

不过虽然有很多的瑕疵（和现实的差距过于大），但是作为学习的demo，还是非常好的。

感谢那位师兄分享，和原作大神的分享。