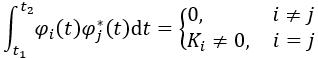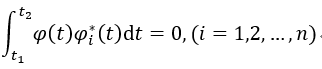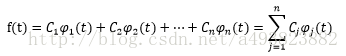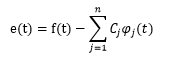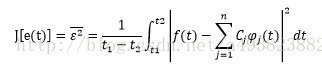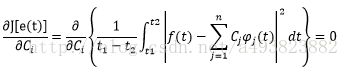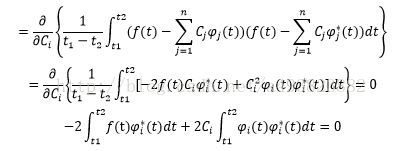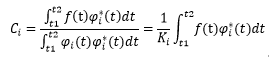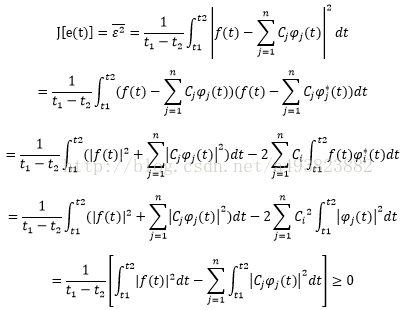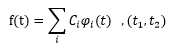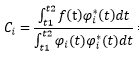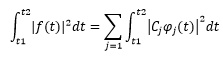完备正交集，函数/信号的正交分解

1.矢量正交与正交分解

信号分解就是将信号表示成一组相互正交的信号分量之和。

由矢量空间理论可知，任意N维矢量可由N维正交坐标系表示。以二维矢量为例，坐标可表示为

ex与ey为x轴和y轴方向的基向量

满足两个性质：①正交性②单位模特性

矢量空间正交分解的概念可推广到信号空间：类似于任意矢量可以表示为正交基函数的线性组合，在信号空间找到若干个相互正交的信号作为基本信号，任意信号也可以表示为正交波形的加权组合。

2.函数正交与正交函数集

若n个函数φ1(t),φ2(t),...,φn(t)构成一个函数集，当这些函数在区间(t1,t2)内满足：

则此函数集为在区间(t1,t2)的正交函数集。

对应于矢量分解，i≠j的特性对应于正交性，i=j对应于单位模特性

如果在正交函数集{φ1(t),φ2(t),...,φn(t)}之外，不存在任何函数φ(t)(≠0)能够满足正交条件：

则称此函数集为区间(t1,t2)上的完备正交函数集。

三角函数集{1,cos(Ωt),cos(2Ωt),...,sin(Ωt),sin(2Ωt),...}与虚指数集{e^jΩnt, n∈Z}都是在(t0,t0+T)(t=2π/Ω)上的完备正交函数集。

3.函数（信号）的正交分解

与空间矢量的正交分解相类似，可将（连续时间信号）函数f(t)进行正交展开。

将任一函数f(t)用n个正交函数（φi(t)）的线性组合来近似，可表示为：

估计量的误差定义为：

需使误差最小，采用最小均方误差准则（误差的方均值最小）。估计值的均方误差定义为：

为使上式最小（系数Cj变化时，即Cj为变量），有Leibnitz准则（求偏导等于0处取最小值），有：

继续对原式化简，将与Ci无关的项除去后得：

所以此时欲使均方误差最小，第i项φi的系数Ci应该如下取值：

此时的均方误差为：

由均方误差的定义式可见，由于函数平方后再积分，因而J[e(t)]不可能为负，即恒大于等于0。

由上式可见，再用正交函数去近似f(t)时，所取的项数越多，即n越大，均方误差则越小。当n→∞时（完备正交函数集），均方误差为0。

所以关于完备正交函数集有如下两个定理：

（1）任何一个信号f(t)都可以在区间(t1,t2)内精确地表示为这个完备正交函数集中各函数的线性组合，即

其中Ci为加权系数，Ci为

上式称为正交展开式，有时也称为广义傅里叶级数，Ci称为傅里叶系数。

注：若基函数满足单位正交性且为实数，即(如，三角函数集满足此条件），那么可写作：

（2）在（1）的条件下，根据此时均方误差为0，可得：

这就是帕塞瓦尔（Parseval）方程（等式）。它表明，在区间(t1,t2)，信号f(t)的能量恒等于f(t)在完备正交函数集中分解的各正交分量能量之和。