感知机模型

感知机模型

1. 模型概览

方法：感知机模型
适用问题：二分类
模型特点：分离超平面
模型类型：判别模型
学习策略：极小化误分点到超平面距离
损失函数：误分点到超平面距离
学习算法：随机梯度下降法

2. 模型介绍

感知机(perceptron)是处理二分类的线性分类模型。感知机旨在求出将训练数据进行线性划分的分离超平面，属于判别模型，所以，导入误分类的损失函数，利用梯度下降法极小化损失函数，求得感知机模型，感知机预测是用学习得到的感知机模型对新输入的数据进行分类。感知机在1957年由Rosenblatt提出，是神经网络和支持向量机的基础。

3. 模型定义

由输入空间到输出空间的如下函数：

f(x)=sign(w⋅x+b)

称为感知机。其中w为权重，b为偏置，sign为符号函数：

sign(x)={+1,x≥0−1,x<0

所以，感知机输出是{+1，-1}.

几何解释：
线性方程

wx+b=0

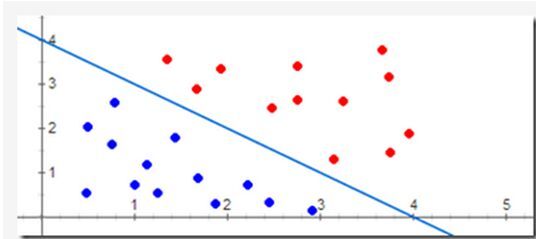
对应特征空间的一个超平面S，其中w为该平面的法向量，b为超平面的截距。这个超平面将特征空间分为两个部分，位于两部分的点分别被分为正负两类，因此，超平面S被称为分离超平面。如下图所示：

4. 感知机学习策略

首先解释一下什么是线性可分：对包含正负样例点的集合T，如果存在一个超平面S能够将所有正负样例点完全分在平面两侧，则称T为线性可分的，否则为线性不可分。感知机模型就是假设训练集合为线性可分的。

接下来我们定义损失函数，并将其最小化。感知机模型的损失函数为所有误分类点到超平面的距离和，这很好理解。不选择误分类点的个数是因为，它不是w,b的连续可导函数，不好优化。损失函数形式如下：

L(w,b)=−∑xi∈Myi(w⋅xi+b)

我们来推导一下：
空间任意点 x0 到超平面S的距离为：

1∥w∥|w⋅x0+b|

这里 ∥w∥ 为w的二范数。
其次，对于误分类的数据 (xi,yi) 来说

−yi(w⋅xi+b)>0

因为 |yi|=1 ，对于误分点数据 (xi,yi) 有：

|w⋅xi+b|=|yi(w⋅xi+b)|=−yi(w⋅xi+b)

所以误分类点到超平面距离可以表示为：

−1∥w∥yi(w⋅xi+b)

假设误分类点集合为M，那么所有误分类点到超平面S的距离和为

−1∥w∥∑xi∈Myi(w⋅xi+b)

不考虑 1∥w∥ ，就得到感知机模型的损失函数：

L(w,b)=−∑xi∈Myi(w⋅xi+b)

为什么不考虑 1∥w∥ ？
网上有人说 1∥w∥ 是个定值，但是个人觉得平面不唯一，这个值肯定也会变。通过参考他人观点结合思考，觉得原因可以列为以下两点，如果有更好见解的朋友欢迎讨论！

1、 1∥w∥ 不影响 yi(w⋅xi+b) 正负的判断，即不影响学习算法的中间过程。因为感知机学习算法是误分类驱动的，这里需要注意的是所谓的“误分类驱动”指的是我们只需要判断 −yi(w⋅xi+b) 的正负来判断分类的正确与否，而 1∥w∥ 并不影响正负值的判断。所以 1∥w∥ 对感知机学习算法的中间过程可以不考虑；

2、 1∥w∥ 不影响感知机学习算法的最终结果。因为感知机学习算法最终的终止条件是所有的输入都被正确分类，即不存在误分类的点。则此时损失函数为0. 对应于 −1∥w∥∑xi∈Myi(w⋅xi+b) ，即分子为0.则可以看出 1∥w∥ 对最终结果也无影响。

综上所述，即使忽略 1∥w∥ ，也不会对感知机学习算法的执行过程产生任何影响。反而还能简化运算，提高算法执行效率。

5. 感知机模型的学习算法

感知机学习算法是对上述损失函数进行极小化，求得w和b，采用的方法为随机梯度下降法。目标函数如下：

minL(w,b)=−∑xi∈Myi(w⋅xi+b)

首先任取一个超平面 (w0,b0) ,然后用梯度下降法不断极小化目标函数，过程中不是一次使M中所有误分类点的梯度下降，而是随机选取一个误分类点使其梯度下降。
假设误分类点集合M是固定的，那么损失函数 L(w,b) 的梯度由

∇wL(w,b)=−∑xi∈Myixi

∇bL(w,b)=−∑xi∈Myi

给出（求偏导）。
更新公式如下：

w←w+ηyixi

b←b+ηyi

其中 η （0< η <=1）为步长，也称为学习率。这样通过迭代可以期待损失函数不断减小，直到为0. 注意，感知机。算法由于采用不用的处置或选取不同的误分类点时，解可以不同。

6. 证明算法收敛性

现在证明，对于现行可分数据集感知机学习算法收敛，即经过有限次迭代可以得到一个将训练数据集完全正确划分的分离超平面及感知机模型。

为了便于叙述和推导，将偏置b并入权重向量w，记作 w^=(wT,b)T ，同时将输入向量加以扩充，加入常数1，记作 x^=(xT,1)T 。 这样 x^∈Rn+1,w^∈Rn+1 ，则 w^⋅x^=w⋅x+b 。

通过证明Novikoff定理证明感知机算法的收敛性

假设训练数据集T是线性可分的。 T={(x1,y1),(x2,y2),⋯,(xN,yN)} 其中 xi∈Rn . yi={+1,−1} . i=1,2,⋯,N .
则
(1) 存在 ∥∥w^opt∥∥=1 的超平面 w^opt⋅x^=wopt⋅x+bopt=0 将训练数据集完全分开，且存在 r>0 ，对所有 i=1,2,⋯,N 。

yi(w^opt⋅x^i)=yi(wopt⋅xi+bopt)≥r

(2) 令 R=max∥x^i∥. 则在训练集上感知机算法的误分类次数 k 满足

k≤(Rr)2

证明过程如下：

本文源于个人在进行技术积累时的笔记及思考，有任何问题或更好的见解欢迎讨论！