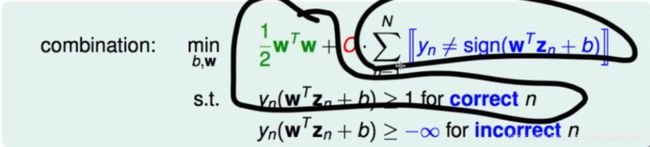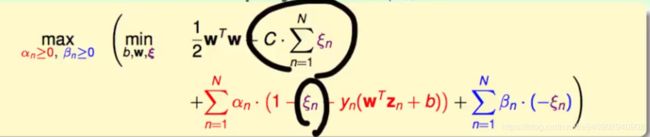SVM与核函数

核函数
核函数

核技巧与SVM

SVM原本是用来解决二分类的分类模型
它和感知机不同的一点是它取到的分类器是在特征空间上的最大间隔的分类器
而为了解决非线性的分类问题 SVM使用核技巧 所以在SVM中核函数的作用是解决了SVM无法处理非线性可分的问题

核函数本质

1.在实际数据上经常遇到线性不可分的情况 而解决方法是将特征映射到更高维的空间去(为什么低维度线性不可分的情况映射到高维度就可以分了？).
2.凡是遇到线性不可分的情况 一律映射到高维度空间 会出现维度爆炸的情况
3.核函数虽然也是将特征进行从低维到高维的转化 但是是在低维上进行计算 而实际的效果表现在高维上 解决了维度爆炸的问题

线性可分的SVM与硬间隔最大化

对于SVM而言 在特征空间中 分类超平面为
wx+b=0
对应的决策函数 为
f=sign(wx+b)
SVM目标是得到分类超平面 wx+b=0 使得所有样本距离分类超平面距离尽量大 分类样本距离分类超平面的距离可以表示分类预测的确信程度 距离越大 确信度越大

即距离分类超平面距离最近的样本 距离分类超平面的距离尽量大（距离分类超平面最近的样本 即支持向量）

当得到固定的分类超平面 即 w，b 固定的时候 对于任意的x |wx+b|可以相对的表示对于某一个x的分类置信程度 当分类超平面固定的时候 |wx+b| 越大 说明其距离分类超平面越远 例如 w，b 固定 若 |wx₁+b| 小于 |wx₂+b| 则说明 对于该分类超平面 x₂ 的分类置信度更高

此时只讨论了样本到分类超平面的距离 没有讨论是否被正确分类 因此需要加上一个限制条件 y_i (wx_i+b) >0

根据之前SVM的目的 即 最大化间隔

那么对于所有的x
max(min _i=1,2…N |wx_i+b| )
s.t. y_i (wx_i+b) >0

对于线性可分的SVM
上述条件可以改写为
max_w,b (min_i=1,2…N y_i(wx_i+b) )
(上述式子可以想象成 给定一组 w,b 该w,b 满足 y_i (wx_i+b) >0 对于所有的x 存在一个y_i(wx_i+b) 的最小值 记录下该最小值 对于所有的满足条件的w,b 选择最小值最大的一种 w,b )

但是上述式子有一个问题 即 成比例的更改w和b 分类超平面是不会改变的 但是 最小距离却会改变 假设此时我们找到了一组 w,b 使得该w,b 在所有x上的最小值最大 但是如果不对w和b的大小做限制 这是不可能实现的 因为一旦发现了这样的w和b 我们将w，b修改为 2w和2b 那么 min_i=1,2…N y_i(wx_i+b) 也就变成原来的两倍 虽然找到的超平面还是原来的超平面 但是 这样 max_w,b (min_i=1,2…N y_i(wx_i+b) )是不可能能求出最优的w和b的

通过上述直观的感觉可以发现 找不出最优的w和b的根源是不限制w和b的大小 明明已经找到最优超平面 就是无法输出最优的w和b 那么解决方法自然就是现在w和b的大小 很自然的限制一个向量的大小不改变该向量的方法就是对向量进行归一化
即w和b分别处以|w| 进行归一化
此时 目标函数变成
max_w,b (min_i=1,2…N y_i(wx_i+b)/||w|| )

这就是几何间隔，之所以叫做几何间隔 是因为其自身的几何意义
假定我们已经拥有这样一个平面
w^Tx+b=0 求 distance（x,w,b）

假设x^’和x^’’ j均为平面上的点 那么
w^Tx^’=-b 同理 w^Tx^‘’=-b
所以w^T(x^’-x^’’)=0 说明w垂直于平面上任意直线 即 w为平面的法向量
而点到平面的距离为 (x-x^’) 投影到垂直于平面的方向 即w的方向

(下述转化过程很容易忘记)
推导至此 线性可分的SVM 优化目标函数 即最大化间隔 也就是使得几何间隔最大
将几何间隔记做 γ_i=y_i（wx_i+b）/||w||
最小几何间隔 γ=min γ_i

max _w,b γ
s.t. y_i（wx_i+b）/||w||>=γ
（接下来的一步转化很关键）

根据几何间隔和函数间隔的关系
即函数间隔/||w|| 等于几何间隔
所有上述优化目标函数可以转化为
max_w,b γ^’ /||w||
s.t. y_i（wx_i+b）>=γ^’

函数间隔不会影响最终最优解的求解 既然函数间隔不会影响最优解求解 那么赋予函数间隔任何值 都会得到一个和原始问题等价的最优解问题
因为之前依旧推导了 函数间隔是随着w和b改变而改变的 当w和b 增大λ倍 函数距离也增大λ倍 所以不妨去γ_’ 等于一

(第二步转化)
将 max_w,b γ^’ /||w|| 转化为求最小值
min_w,b1/2||w||²
s.t. y_i（wx_i+b）-1>=0

当取到最优解w和b时 对于y=1 的点 支持向量在超平面 wx+b=1上
对于y=-1的点 支持向量在超平面 wx+b=-1 上
间隔等于 2/||w||

所以总结一下 SVM是一个具有n个条件的最小化问题 （因为对于每一个x都需要满足 y_i（wx_i+b）-1>=0 如果具有n个x 则有n个限制条件）

SVM对偶算法

为什么要使用对偶算法
1.对偶算法更易求解
2.对偶算法方便使用核技巧 解决非线性可分的问题

首先对于原始的SVM
min_w,b1/2||w||²
s.t. y_i（wx_i+b）-1>=0
如果x在原始的特征空间不是线性可分的 那么我们可以对x进行非线性转化
z_{n=Φ(xn)
将原始空间转化为z空间
但是这样就有一个问题 在直接将原始特征映射到z空间 很容易造成特征的爆炸
所以有没有其他的方法解决这一问题呢 这一就引出了SVM对偶问题}

使用拉格朗日乘子 将条件和最小化目标函数相结合
对于原始的SVM

（这里将x映射到z空间 ）
对于每一个限制条件都对应一个拉格朗日乘子
所以将目标函数与条件结合可得

其中拉格朗日乘子大于等于0

那么原来带有限制的目标函数就转化为
min_w,b(max _α1/2 w^Tw+∑ α（1-y_n(w^Tz_n+b)）)
为什么上述带有限制的目标函数和转化后的目标函数是等效的呢？
上述式子分为两种情况

1. 如果上述的w，b不是满足转化之前的限制的话 即1-y_n(w^Tz_n+b) 大于0 乘上α依然大于0 那么对于任意给定的w，b max _α1/2 w^Tw+∑ α（1-y_n(w^Tz_n+b)）都是无穷大
2. 如果 w，b 满足限制 即1-y_n(w^Tz_n+b) <=0 那么乘上一个非负的α最小值为0 此时
   相当于求 min_w,b1/2 w^Tw 即为带限制的目标函数
   最小化肯定不会选无限大的 所有肯定会选择一个符合条件的有限大的结果 即 和原来转化之前一致

此时已经将原来的SVM转化为一个新的优化的目标函数
min_w,b(max _α1/2 w^Tw+∑ α（1-y_n(w^Tz_n+b)）)

接下来继续转化
对于固定的α^’ min_w,b 1/2 w^Tw+∑ α^’（1-y_n(w^Tz_n+b) <= min_w,b(max _α1/2 w^Tw+∑ α（1-y_n(w^Tz_n+b)）)
对于所有的固定的α都满足上述的式子
所以
对于其中最大的α也是满足的 即
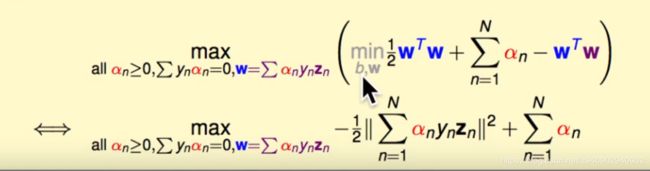
min_w,b(max _α1/2 w^Tw+∑ α（1-y_n(w^Tz_n+b)）)>=max _α (min_w,b 1/2 w^Tw+∑ α（1-y_n(w^Tz_n+b))
即得到拉格朗日对偶问题 如果解决该对偶问题 可以得到原始最佳化问题的下限 （之所以要做这一步转化是因为 我们常常喜欢求解没有条件的最佳化问题 而转化之后的问题求解w和b的部分在内层 不存在额外的条件）
那么什么时候解左边问题和解右边问题是等价的呢 即拉格朗日对偶问题具有强对偶关系 即左侧不仅仅是大于等于右侧 而是等于的关系
那么什么时候原始问题和对偶问题相等呢（参考统计学习方法 拉格朗日对偶）？
1.最小化的目标函数是凸函数 在SVM中 最小化的为 min_w,b 1/2 ||w||² 刚好是凸函数
2. 原来的问题有解 即对于所有的x 在z空间线性可分 即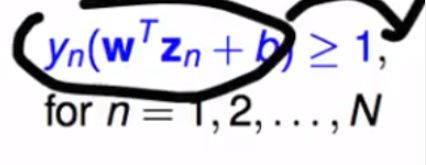
对于所有的zn都满足

既然具有强对偶关系 那么就可以对SVM的对偶函数求极值

此时先求内层不具有条件限制的最小化问题 很简单 不具有条件限制的最小化问题可以通过求偏导 极值处偏导为0 获得
首先是对b求偏导

所以最佳解满足上述条件 既然最佳解满足上述条件 可以将该条件加入到最佳化的式子中 即

可以看到如果∑α_ny_n =0 其实就是b的系数为0 那么可以将b省去（这里有一个问题 如果将b消掉之后怎么做hypothesis的预测 之后会说）

整理可得

接下来对w求偏导 因为w是一个向量 对于向量求偏导 相当于对向量中的每一个元素求偏导

所以最佳解要满足的w的限制为

使用和上述一样的技巧将w代入

因为w可以用α表示 所以可以直接消掉min 求得外层的max 即可得到w
所以整理可得最佳化问题变成上述式子

所以进一步来看 究竟是满足哪些条件才让我们得到了上述看上去较为简单的表达式

1. 第一个条件是我们在使用函数间隔代替集合间隔的时候要满足的限制
2. 第二个是拉格朗日算子要满足的限制
3. 第三是推导出的对于w和b偏导等于0满足的限制
4. 第四个是使用拉格朗日算子将带限制的优化目标函数转化为不带限制的优化目标函数满足的限制
   所以得出α 的最佳解之后可以使用这些条件反推出w和b

将上述的平方项展开 求相反数取最小可得
（α₁y₁z₁ +α₂y₂z₂+…+α_ny_nz_n）乘以 （α₁y₁z₁ +α₂y₂z₂+…+α_ny_nz_n） 展开相当于任意两个相乘再相加
又因为w=∑α_ny_nz_n 是关于w和α的关系 与最小化无关 可以在求下述最小化式子的时候先省去
可得

通过二次规划可以解α 那么假设当我们得到α之后如何反求得w和b呢

w很好求

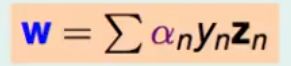
但是b怎么求呢


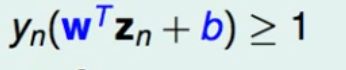
如果αn大于0 那么
(1-y_n(w^Tz_n+b))=0
又因为 y为1或者-1
所以b=y_n-w^Tz_n

根据之前的推导 如果 y_n(w^Tz_n+b)=1 那么这个点在边界上 即该点为support vevtor
这样一个好处就是 求w的时候是所有点关于α的线性组合 如果α等于0 那么 加进去没有意义 所以可以只用加α不为0的点 即support vector的点
因此w和b都可以通过support vector算出
最终结果为
f(x)=sign(wx+b) 即
f(x)=∑_SVα_ny_nz_nx+(y_n-w^Tz_n)

这里观察SVM求解出的最终的w 为y_nz_n 关于α的线性组合
和PLA十分相似 PLA每犯错一次 就会加上一次y_nx_n
如果PLA的w初始值为0 则可以表示为右下所示

由此可见 SVm和PLA中的w都可以用训练样本表示出了 SVM使用support vector表示 而PLA使用犯错的点表示

核技巧

给定两个向量 x_i,x_j 计算两个向量的内积 I= i,x_j>
通过某种非线性变化 x----> Φ(x) ,将x映射到高维空间中 ，映射之后内积变为 I^’=<Φ(x_i),Φ(x_j)> , 此时内积如何计算呢？
如果按照传统的方法 先将x 映射到高维空间 然后将映射之后的x做内积 那么会有计算量复杂的问题
那么能否在原始的空间中寻找一个函数 K( x_i,x_j ) = <Φ(x_i),Φ(x_j)>
即简化计算映射后内积的计算 这样的简化方法称为核技巧 而函数K则称为核函数

SVM可以处理线性可分的情况 而对于线性不可分的情况 SVM会借助核函数 将当前线性不可分的数据映射到高维空间
以达到线性可分的目的

将特征转化比较常用的方式是多项式的转化
这里以二次多项式作为例子
如果我们转化到的空间是二次空间 即

由此可见 可以不用先求特征转化 再求内积 而是 只需要先在原始的空间内做内积 代表在特种空间中做内积

通过上述特殊的例子可知 我们可能能够在原始的特征空间中进行计算 就能够表征转换后的特征空间
凑巧的是在SVM对偶形式中 全部求解的过程都使用到了特征转化之后的内积

在求解b和w的时候其实只是与support vector的个数有关 因为不是support vector的数据 其对应 的α都为0

这里如果把上述的多项式核做一个推广

可以得到Q次的转化

高斯核

对于高斯核函数
K(x,x^’)=exp(-||x-x^’||²)
为了例子简单起见 我们这里使用x，x^’ 都是一维的
则上述式子变成
K(x,x^’)=exp(-（x-x^’)²) =exp(-x²)exp(-x^’2)exp(2xx^’)
又因为指数函数的泰勒展开如下

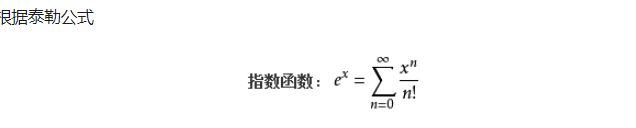
整理可得

这就相当于把原始的转化推广到无限多维 原来只有一维 现在变成了 括号中的无线多维
因此这个高斯函数 相当于里面隐藏了无限多维转化的

因此得到多个 中心在support vectpor上的高斯函数的线性组合

在不使用核函数的时候 如果我们想要通过线性分类器分类非线性的样本 需要选择一个新的特征集，并且将原始的特征写成新的特征的形式 这就相当于使用一个固定的映射函数 将数据映射到对应的特征空间 并在该特征空间中使用线性分类器分类，而使用核函数可以减小计算量
以SVM为例（这里假设已知 SVM 对偶形式 至于SVM 对偶形式是如何推导得出的以及 为什么要使用SVM的对偶形式 结合 台大课程 明天给出结论）
把原始的SVM转化为如下形式 会发现有一个求内积的运算 而核函数就是在这里进行的影响

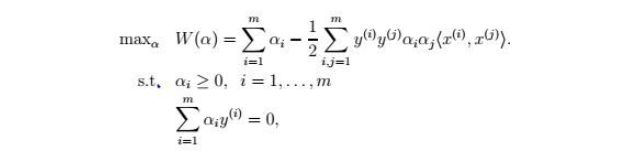
多种不同的核函数比较

到这里对于核函数特别是线性核函数存在的意义又有点模糊了
线性核：不会对原始特征空间进行转化 只能进行线性可分的数据
多项式核函数： Q不可以过大 同时需要选择的参数有三个

注：kernel其实是相似性的度量 因为 内积本来就是对于两个向量相似性的度量手段
对于自定义的kernel是合法的充要条件是 1.对称 2.半正定（这里还有待继续强化）

soft margin 问题

这里借用pocket的思想 Pocket 优化的目标是使得错误分类的总数最小

将优化函数分成两部分 一部分是可以被正确分类的
可以正确分类的部分还是一样的
对于不能被正确分类的部分
即y_n ≠ sign(w^Tz_n+b)
并为其赋权重为C 代表该项所占比重

但是写成如上的式子有问题
1.限制条件包含是非判断 不是线性的 因此无法对其进行对偶 核技巧的实施
2.上述式子只能表征是否犯错 而无法表征犯错的程度

因此我们需要记录的内容应该由犯了几个错误转化为犯了多大的错误
我们使用ζ记录犯错的大小

C越大表示对错误的容忍度越小 C越小说明错误出现没有太大关系 但是margin要大

得到soft margin的表达之后 和之前hard margin一样 要对其进行拉格朗日对偶转化

因为现在有了两个不同的限制 需要引入两个拉格朗日对偶参数 α β
拉格朗日对偶函数就是将原始的最小化目标函数 加上∑ α constraint 1 +∑ β constraint2
其中constraint 要转化为 <=0的形式
整理得

同样的通过最大最小

对于ζ求偏导可得

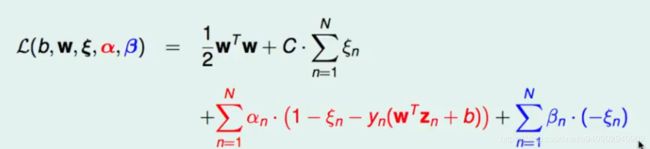
这样可以将β表示成C和α
这样表示增加了一个限制 即β>=0 那么 C-α也要>=0 因此
整理可得

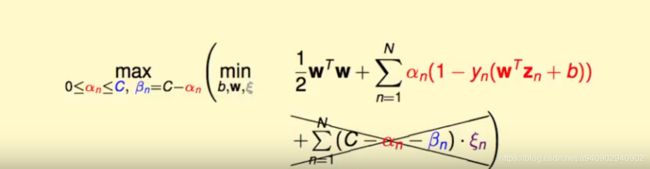
会发现这时和hard margin其实十分相似 唯一的不同就是增加了α的上限
这时对w和b求偏导 和hard margin是一摸一样的

以二维空间为例

假设映射是将二维空间映射为五维空间 即 (x₁,x₂) 映射为 (x₁,x₂,x₁x₂,x₁² ,x₂²) 然后在做内积 对应位置相乘再相加 得到上述式子
由此可见 当给定映射的时候 将特征先映射到对应的特征空间 然后再在该特征空间中求内积的运算量 要大于 在映射之前的特征空间求内积 然后再计算出K