层次分析法---python实现

层次分析法（The analytic hierarchy process）简称AHP

在20世纪70年代中期由美国运筹学家托马斯·塞蒂（T.L.saaty）正式提出。它是一种定性和定量相结合的、系统化、层次化的分析方法。由于它在处理复杂的决策问题上的实用性和有效性，很快在世界范围得到重视。它的应用已遍及经济计划和管理、能源政策和分配、行为科学、军事指挥、运输、农业、教育、人才、医疗和环境等领域。

比较常用的场合是进行决策，层次分析法是一种比较常见的多目标决策方法。其实我看来，层次分析法就是一种按照层次结构计算加权和的方法，主要是权重的选取，这里人为因素太大，比较容易受到诟病。

具体的理论，可以参考wiki，附上网址：https://wiki.mbalib.com/wiki/%E5%B1%82%E6%AC%A1%E5%88%86%E6%9E%90%E6%B3%95

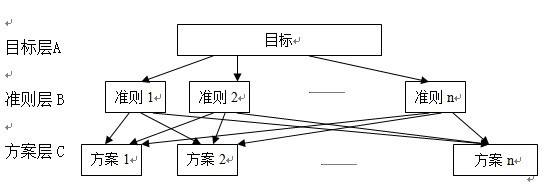
层次分析法的多级递阶层次模型分为三类：完全相关性结构、完全独立性结构、混合型结构。

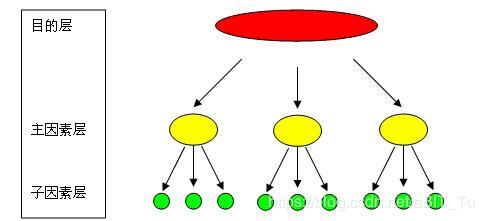
前两种分别对应于下图的图1，2（来自网络，侵删）：

                                 

                                                                                 图1 . 完全相关性

                                         

                                                                                 图2. 完全独立性

混合型就是具备两种的特点。其实也不需要管这个了，就是按照自己的需要搭建好层次结构就可以了，有了结构下面开始撸代码。

示例：

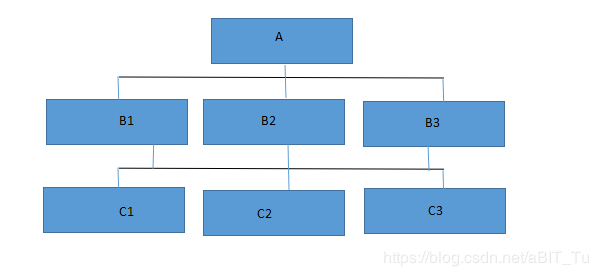
此次我们实现的是这样的层次结构，如图3，同时我们假设成对比较矩阵已经按照尺度表定义好（尺度表即表示相对权重，在wiki中可以找到），实际应用中可以根据需求求解成对比较矩阵。

                                   

                                                                             图3. 示例的层次结构图

python3 代码。

# -*- coding: utf-8 -*-
"""
Created on Tue Nov 13 15:37:12 2018

@author: user
"""

"""
AHP demo: 第一层：A, 第二层：B1 B2 B3, 第三层：C1 C2 C3, 完全相关性结构。
"""

import numpy as np

"""
1. 成对比较矩阵 
"""
def comparision(W0):  # W为每个信息值的权重
    n=len(W0)
    F=np.zeros([n,n])
    for i in range(n):
        for j in range(n):
            if i==j:
                F[i,j]=1
            else:
                F[i,j]=W0[i]/W0[j]
    return F
                
"""
2. 单层排序,相对重要度
"""
def ReImpo(F):
    n=np.shape(F)[0]
    W=np.zeros([1,n])
    for i in range(n):
        t=1
        for j in range(n):
            t=F[i,j]*t
        W[0,i]=t**(1/n)
    W=W/sum(W[0,:])  # 归一化 W=[0.874,2.467,0.464]
    return W.T

"""
3. 一致性检验
"""
def isConsist(F):
    n=np.shape(F)[0]
    a,b=np.linalg.eig(F)
    maxlam=a[0].real
    CI=(maxlam-n)/(n-1)
    if CI<0.1:
        return bool(1)
    else:
        return bool(0)
"""
4. 计算综合重要性
"""
def ComImpo(W12,W231,W232,W233):  # 综合重要性
    #F12=comparision(W12)  # 实际应用中可以根据特征的权重求解成对比较矩阵。
    #F231=comparision(W231)
    #F232=comparision(W232)
    #F233=comparision(W233)
    F12=np.array([[1,1/3,2],[3,1,5],[1/2,1/5,1]])  # 此处直接假设出成对比较矩阵
    F231=np.array([[1,1/3,1/5],[3,1,1/3],[5,3,1]])
    F232=np.array([[1,2,7],[1/2,1,5],[1/7,1/5,1]])
    F233=np.array([[1,1/3,1/7],[3,1,1/5],[7,5,1]])
    
    if isConsist(F12) and isConsist(F231) and isConsist(F232) and isConsist(F233):
        W12=ReImpo(F12)
        W231=ReImpo(F231)
        W232=ReImpo(F232)
        W233=ReImpo(F233)
        W23=np.hstack([W231,W232,W233])
    else:
        print("成对比较矩阵不一致，请调整权重后重试！")
        return 0
    n=len(W12)
    C=np.zeros([1,n])
    for i in range(n):
        t=W23[i,:]
        C[0,i]=sum((W12.T*t)[0])
    return C

def main():
    print("这里是AHP的演示程序：")
    w=np.ones([3])  # W 为成对比较矩阵
    C=ComImpo(w,w,w,w)
    print('最佳方案为第',np.argmax(C)+1,'个方案.','综合推荐指数为',max(C[0,:]))



if __name__ == '__main__':
    main()
    # print(__name__)