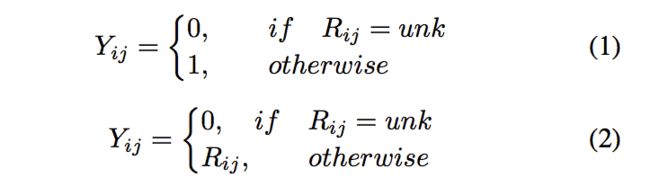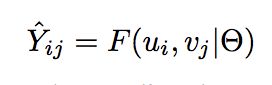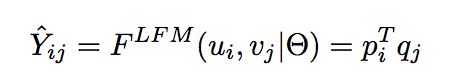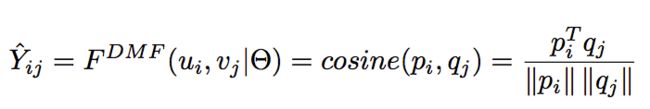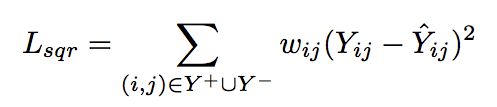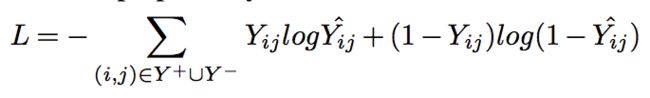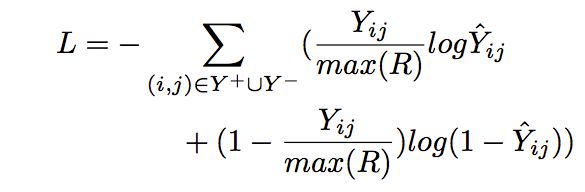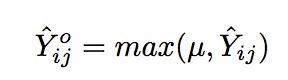推荐系统遇上深度学习(三十)--深度矩阵分解模型理论及实践
本篇为推荐系统遇上深度学习系列的第30篇文章,也是2019年以来的第一篇文章,2019年希望该系列能够到50篇!加油!
本文提出了一种基于神经网络结构的矩阵分解模型。该模型综合考虑了用户对物品的显式评分和非偏好隐式反馈,然后通过两组神经网络将用户和物品的特征提取到一个低维空间;并通过设计的新的损失函数进行反向学习。本文设计的新损失函数将显式反馈加入二元交叉熵损失函数中,称为归一化交叉熵损失。实验证明该模型在几个典型数据集上相对于其他经典模型表现更好。
论文题目为:《Deep Matrix Factorization Models for Recommender Systems》
论文地址为:https://www.ijcai.org/proceedings/2017/0447.pdf
本文提出的模型名称为Deep Matrix Factorization Models,下文我们简称DMF
1、DMF原理介绍
1.1 问题陈述
假设我们有M个用户以及N个物品,R是M*N的评分矩阵,Rij表示用户i对于物品j的评分。在实际中,我们有两种方式来构造用户-物品交互矩阵Y(实际中用于训练的矩阵):
大部分现有的方案中,使用(1)来构建交互矩阵Y,但本文使用(2)来构建交互矩阵。如果用户i对物品j有评分,那么Yij=Rij,此时反馈被称为显式反馈。否则的话,Yij=0,此时我们称这种反馈为非偏好隐式反馈(non-preference implicit feedback)(个人理解是评分为0不代表用户不喜欢,可能是用户没有接触过该物品)。
推荐系统的任务往往是对交互矩阵中未知的部分进行评分,随后对评分的结果进行排序,我们假定评分通过一个模型来得到:
如何定义一个F呢?举例来说,隐语义模型(LFM)简单地应用pi,qj的点积来预测:
那么,DMF是如何构建F的呢?在介绍之前,我们先介绍一下一些有用的符号:
Y:交互矩阵
Y+:Y中观测到的交互,即显式反馈
Y-:Y中的全部0元素
Y-sampled:负样本,可以是Y-,也可以是Y-的部分采样
Y+ ∪ Y-sampled:所有训练样本
Yi*:交互矩阵中的第i行,表示用户i对所有物品的评分
Y*j:交互矩阵中的第j列,表示所有用户对物品j的评分
2.2 DMF模型
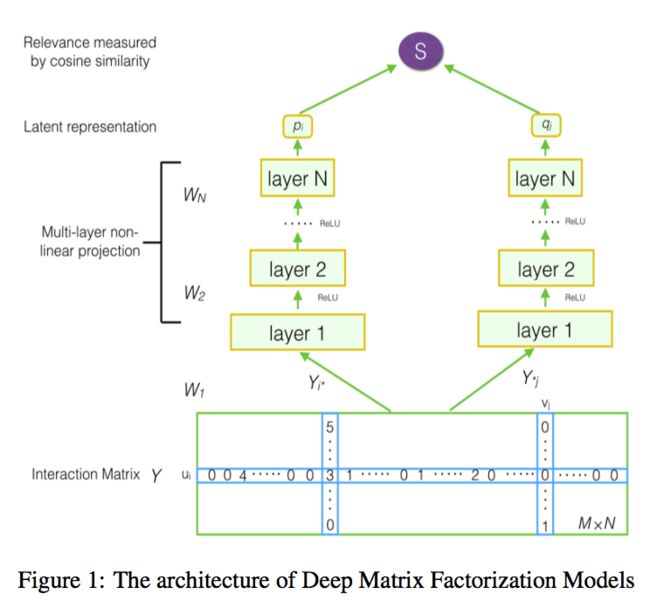
DMF模型框架如下:
可以看到,为了预测用户i对物品j的评分,用户i的输入是交互矩阵中的第i行Yi*、物品j的输入是交互矩阵中的第j列Y*j。两部分的输入分别经过两个多层神经网络得到向量pi和qj,即用户i和物品j的隐向量表示。
随后,通过pi和qj的余弦距离得到预测评分:
论文中指出,这是第一次直接使用交互矩阵作为表示学习的输入。正如我们前面提到的,Yi*代表用户对所有物品的评分。它可以在某种程度上表明用户的全局偏好。Y*j代表了一个物品上所有用户评价。它可以在某种程度上表明一个物品的概要。论文中认为用户和项目的这些表示对于最终的低维表示非常有用。
2.3 损失函数设计
对于推荐系统来说,主要有两种目标函数,一是point-wise的,二是pair-wise的,本文使用point-wise的目标函数。目标函数中最重要的部分就是损失函数。
在许多现有的模型中,对于显式反馈,使用平方损失函数:
但是平方损失函数对于隐式反馈来说并不是十分有效。隐式反馈通常被视作0-1二分类问题,通常使用交叉熵损失函数:
本文构造的交互矩阵,既有显示评分,也有隐式反馈。而平方损失关注显式评分,而交叉熵损失则关注隐式反馈。所以本文提出了归一化交叉熵损失函数,将显式的评分合并到交叉熵损失中。该损失函数的计算公式如下:
max(R)是所有评分中的最大值。还有一个注意的点是,预测值不能是负数,所以我们要对负数进行处理,使其变为一个非常小的数:
综上,DMF的过程如下:
2、DMF代码实现
代码地址为:https://github.com/princewen/tensorflow_practice/tree/master/recommendation/Basic-DMF-Model
数据为movieslen-1m的数据:https://grouplens.org/datasets/movielens/
代码实现非常简单,这里我们简要介绍一下模型的构建过程:
定义placeholder
placeholde主要有用户id、物品id、评分以及dropout的值:
def add_placeholders(self):
self.user = tf.placeholder(tf.int32)
self.item = tf.placeholder(tf.int32)
self.rate = tf.placeholder(tf.float32)
self.drop = tf.placeholder(tf.float32)
构造embedding
由于我们直接使用交互矩阵中的一行或者一列作为输入,因此,用户的embedding是交互矩阵,而物品的embedding是交互矩阵的转置。下面代码中self.dataSet.getEmbedding()便是交互矩阵:
def add_embedding_matrix(self):
self.user_item_embedding = tf.convert_to_tensor(self.dataSet.getEmbedding())
self.item_user_embedding = tf.transpose(self.user_item_embedding)
接下来,便可以通过embedding_lookup函数来获取模型的输入:
user_input = tf.nn.embedding_lookup(self.user_item_embedding, self.user)
item_input = tf.nn.embedding_lookup(self.item_user_embedding, self.item)
两部分全连接网络
对于得到的user_input和item_input,通过两部分全连接网络得到隐向量表示:
with tf.name_scope("User_Layer"):
user_W1 = init_variable([self.shape[1], self.userLayer[0]], "user_W1")
user_out = tf.matmul(user_input, user_W1)
for i in range(0, len(self.userLayer)-1):
W = init_variable([self.userLayer[i], self.userLayer[i+1]], "user_W"+str(i+2))
b = init_variable([self.userLayer[i+1]], "user_b"+str(i+2))
user_out = tf.nn.relu(tf.add(tf.matmul(user_out, W), b))
with tf.name_scope("Item_Layer"):
item_W1 = init_variable([self.shape[0], self.itemLayer[0]], "item_W1")
item_out = tf.matmul(item_input, item_W1)
for i in range(0, len(self.itemLayer)-1):
W = init_variable([self.itemLayer[i], self.itemLayer[i+1]], "item_W"+str(i+2))
b = init_variable([self.itemLayer[i+1]], "item_b"+str(i+2))
item_out = tf.nn.relu(tf.add(tf.matmul(item_out, W), b))
得到预测评分
预测评分通过计算用户和物品隐向量的余弦距离得到,还要将负数变为一个极小的正数:
norm_user_output = tf.sqrt(tf.reduce_sum(tf.square(user_out), axis=1))
norm_item_output = tf.sqrt(tf.reduce_sum(tf.square(item_out), axis=1))
self.y_ = tf.reduce_sum(tf.multiply(user_out, item_out), axis=1, keep_dims=False) / (norm_item_output* norm_user_output)
self.y_ = tf.maximum(1e-6, self.y_)
损失函数
我们使用归一化的交叉熵损失函数:
def add_loss(self):
regRate = self.rate / self.maxRate
losses = regRate * tf.log(self.y_) + (1 - regRate) * tf.log(1 - self.y_)
loss = -tf.reduce_sum(losses)
# regLoss = tf.add_n([tf.nn.l2_loss(v) for v in tf.trainable_variables()])
# self.loss = loss + self.reg * regLoss
self.loss = loss
好了,代码就介绍到这里了,小伙伴们可以自己动手实现一下,非常的简单。再次祝大家学业顺利,开工大吉!