学习bp神经网络 详细教程
英文出处: iamtrask。欢迎加入 翻译组。
概要:直接上代码是最有效的学习方式。这篇教程通过由一段简短的 python 代码实现的非常简单的实例来讲解 BP 反向传播算法。
代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
|
X
=
np
.
array
(
[
[
0
,
0
,
1
]
,
[
0
,
1
,
1
]
,
[
1
,
0
,
1
]
,
[
1
,
1
,
1
]
]
)
y
=
np
.
array
(
[
[
0
,
1
,
1
,
0
]
]
)
.
T
syn0
=
2
*
np
.
random
.
random
(
(
3
,
4
)
)
-
1
syn1
=
2
*
np
.
random
.
random
(
(
4
,
1
)
)
-
1
for
j
in
xrange
(
60000
)
:
l1
=
1
/
(
1
+
np
.
exp
(
-
(
np
.
dot
(
X
,
syn0
)
)
)
)
l2
=
1
/
(
1
+
np
.
exp
(
-
(
np
.
dot
(
l1
,
syn1
)
)
)
)
l2_delta
=
(
y
-
l2
)
*
(
l2
*
(
1
-
l2
)
)
l1_delta
=
l2_delta
.
dot
(
syn1
.
T
)
*
(
l1
*
(
1
-
l1
)
)
syn1
+=
l1
.
T
.
dot
(
l2_delta
)
syn0
+=
X
.
T
.
dot
(
l1_delta
)
|
当然,上述程序可能过于简练了。下面我会将其简要分解成几个部分进行探讨。
第一部分:一个简洁的神经网络
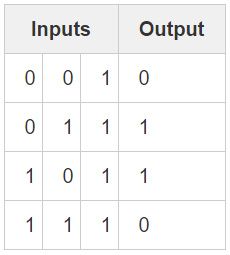
一个用 BP 算法训练的神经网络尝试着用输入去预测输出。
考虑以上情形:给定三列输入,试着去预测对应的一列输出。我们可以通过简单测量输入与输出值的数据来解决这一问题。这样一来,我们可以发现最左边的一列输入值和输出值是完美匹配/完全相关的。直观意义上来讲,反向传播算法便是通过这种方式来衡量数据间统计关系进而得到模型的。下面直入正题,动手实践。
2 层神经网络:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
import
numpy
as
np
# sigmoid function
def
nonlin
(
x
,
deriv
=
False
)
:
if
(
deriv
==
True
)
:
return
x
*
(
1
-
x
)
return
1
/
(
1
+
np
.
exp
(
-
x
)
)
# input dataset
X
=
np
.
array
(
[
[
0
,
0
,
1
]
,
[
0
,
1
,
1
]
,
[
1
,
0
,
1
]
,
[
1
,
1
,
1
]
]
)
# output dataset
y
=
np
.
array
(
[
[
0
,
0
,
1
,
1
]
]
)
.
T
# seed random numbers to make calculation
# deterministic (just a good practice)
np
.
random
.
seed
(
1
)
# initialize weights randomly with mean 0
syn0
=
2
*
np
.
random
.
random
(
(
3
,
1
)
)
-
1
for
iter
in
xrange
(
10000
)
:
# forward propagation
l0
=
X
l1
=
nonlin
(
np
.
dot
(
l0
,
syn0
)
)
# how much did we miss?
l1_error
=
y
-
l1
# multiply how much we missed by the
# slope of the sigmoid at the values in l1
l1_delta
=
l1_error
*
nonlin
(
l1
,
True
)
# update weights
syn0
+=
np
.
dot
(
l0
.
T
,
l1_delta
)
print
"Output After Training:"
print
l1
|
Output After Training:
[[ 0.00966449]
[ 0.00786506]
[ 0.99358898]
[ 0.99211957]]
| 变量 | 定义说明 | |
|---|---|---|
| X | 输入数据集,形式为矩阵,每 1 行代表 1 个训练样本。 | |
| y | 输出数据集,形式为矩阵,每 1 行代表 1 个训练样本。 | |
| l0 | 网络第 1 层,即网络输入层。 | |
| l1 | 网络第 2 层,常称作隐藏层。 | |
| syn0 | 第一层权值,突触 0 ,连接 l0 层与 l1 层。 | |
| * | 逐元素相乘,故两等长向量相乘等同于其对等元素分别相乘,结果为同等长度的向量。 | |
| – | 元素相减,故两等长向量相减等同于其对等元素分别相减,结果为同等长度的向量。 | |
| x.dot(y) | 若 x 和 y 为向量,则进行点积操作;若均为矩阵,则进行矩阵相乘操作;若其中之一为矩阵,则进行向量与矩阵相乘操作。 |
正如在“训练后结果输出”中看到的,程序正确执行!在描述具体过程之前,我建议读者事先去尝试理解并运行下代码,对算法程序的工作方式有一个直观的感受。最好能够在 ipython notebook 中原封不动地跑通以上程序(或者你想自己写个脚本也行,但我还是强烈推荐 notebook )。下面是对理解程序有帮助的几个关键地方:
- 对比 l1 层在首次迭代和最后一次迭代时的状态。
- 仔细察看 “nonlin” 函数,正是它将一个概率值作为输出提供给我们。
- 仔细观察在迭代过程中,l1_error 是如何变化的。
- 将第 36 行中的表达式拆开来分析,大部分秘密武器就在这里面。
- 仔细理解第 39 行代码,网络中所有操作都是在为这步运算做准备。
下面,让我们一行一行地把代码过一遍。
建议:用两个屏幕来打开这篇博客,这样你就能对照着代码来阅读文章。在博客撰写时,我也正是这么做的。 :)
第 1 行:这里导入一个名叫 numpy 的线性代数工具库,它是本程序中唯一的外部依赖。
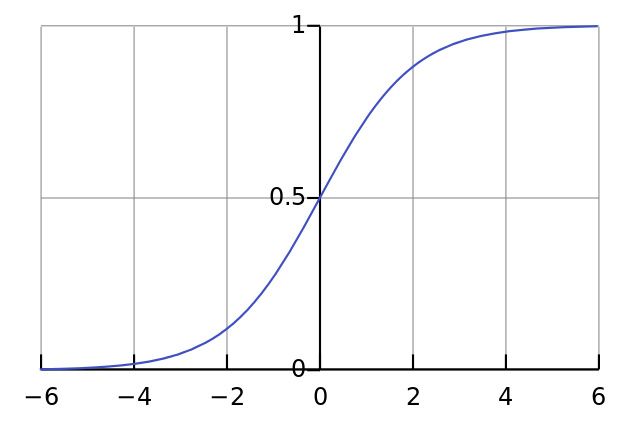
第 4 行:这里是我们的“非线性”部分。虽然它可以是许多种函数,但在这里,使用的非线性映射为一个称作 “sigmoid” 的函数。Sigmoid 函数可以将任何值都映射到一个位于 0 到 1 范围内的值。通过它,我们可以将实数转化为概率值。对于神经网络的训练, Sigmoid 函数也有其它几个非常不错的特性。
第 5 行: 注意,通过 “nonlin” 函数体还能得到 sigmod 函数的导数(当形参 deriv 为 True 时)。Sigmoid 函数优异特性之一,在于只用它的输出值便可以得到其导数值。若 Sigmoid 的输出值用变量 out 表示,则其导数值可简单通过式子 out *(1-out) 得到,这是非常高效的。
若你对求导还不太熟悉,那么你可以这样理解:导数就是 sigmod 函数曲线在给定点上的斜率(如上图所示,曲线上不同的点对应的斜率不同)。有关更多导数方面的知识,可以参考可汗学院的导数求解教程。
第 10 行:这行代码将我们的输入数据集初始化为 numpy 中的矩阵。每一行为一个“训练实例”,每一列的对应着一个输入节点。这样,我们的神经网络便有 3 个输入节点,4 个训练实例。
第 16 行:这行代码对输出数据集进行初始化。在本例中,为了节省空间,我以水平格式( 1 行 4 列)定义生成了数据集。“.T” 为转置函数。经转置后,该 y 矩阵便包含 4 行 1 列。同我们的输入一致,每一行是一个训练实例,而每一列(仅有一列)对应一个输出节点。因此,我们的网络含有 3 个输入, 1 个输出。
第 20 行:为你的随机数设定产生种子是一个良好的习惯。这样一来,你得到的权重初始化集仍是随机分布的,但每次开始训练时,得到的权重初始集分布都是完全一致的。这便于观察你的策略变动是如何影响网络训练的。
第 23 行:这行代码实现了该神经网络权重矩阵的初始化操作。用 “syn0” 来代指 “零号突触”(即“输入层-第一层隐层”间权重矩阵)。由于我们的神经网络只有 2 层(输入层与输出层),因此只需要一个权重矩阵来连接它们。权重矩阵维度为(3,1),是因为神经网络有 3 个输入和 1 个输出。换种方式来讲,也就是 l0 层大小为 3 , l1 层大小为 1 。因此,要想将 l0 层的每个神经元节点与 l1 层的每个神经元节点相连,就需要一个维度大小为(3,1)的连接矩阵。:)
同时,要注意到随机初始化的权重矩阵均值为 0 。关于权重的初始化,里面可有不少学问。因为我们现在还只是练习,所以在权值初始化时设定均值为 0 就可以了。
另一个认识就是,所谓的“神经网络”实际上就是这个权值矩阵。虽然有“层” l0 和 l1 ,但它们都是基于数据集的瞬时值,即层的输入输出状态随不同输入数据而不同,这些状态是不需要保存的。在学习训练过程中,只需存储 syn0 权值矩阵。
第 25 行:本行代码开始就是神经网络训练的代码了。本 for 循环迭代式地多次执行训练代码,使得我们的网络能更好地拟合训练集。
第 28 行:可知,网络第一层 l0 就是我们的输入数据,关于这点,下面作进一步阐述。还记得 X 包含 4 个训练实例(行)吧?在该部分实现中,我们将同时对所有的实例进行处理,这种训练方式称作“整批”训练。因此,虽然我们有 4 个不同的 l0 行,但你可以将其整体视为单个训练实例,这样做并没有什么差别。(我们可以在不改动一行代码的前提下,一次性装入 1000 个甚至 10000 个实例)。
第 29 行:这是神经网络的前向预测阶段。基本上,首先让网络基于给定输入“试着”去预测输出。接着,我们将研究预测效果如何,以至于作出一些调整,使得在每次迭代过程中网络能够表现地更好一点。
(4 x 3) dot (3 x 1) = (4 x 1)
本行代码包含两个步骤。首先,将 l0 与 syn0 进行矩阵相乘。然后,将计算结果传递给 sigmoid 函数。具体考虑到各个矩阵的维度:
(4 x 3) dot (3 x 1) = (4 x 1)
矩阵相乘是有约束的,比如等式靠中间的两个维度必须一致。而最终产生的矩阵,其行数为第一个矩阵的行数,列数则为第二个矩阵的列数。
由于装入了 4 个训练实例,因此最终得到了 4 个猜测结果,即一个(4 x 1)的矩阵。每一个输出都对应,给定输入下网络对正确结果的一个猜测。也许这也能直观地解释:为什么我们可以“载入”任意数目的训练实例。在这种情况下,矩阵乘法仍是奏效的。
第 32 行:这样,对于每一输入,可知 l1 都有对应的一个“猜测”结果。那么通过将真实的结果(y)与猜测结果(l1)作减,就可以对比得到网络预测的效果怎么样。l1_error 是一个有正数和负数组成的向量,它可以反映出网络的误差有多大。
第 36 行:现在,我们要碰到干货了!这里就是秘密武器所在!本行代码信息量比较大,所以将它拆成两部分来分析。
第一部分:求导
|
1
|
nonlin
(
l1
,
True
)
|
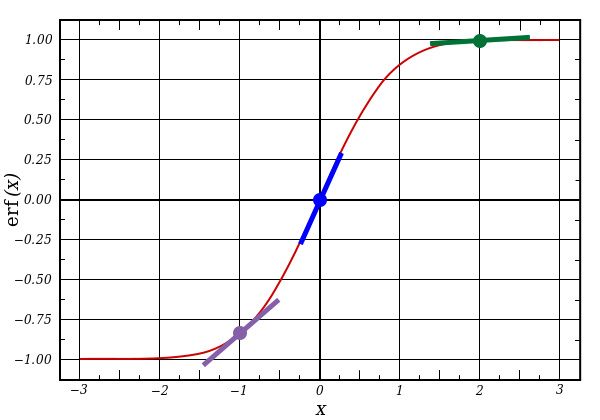
如果 l1 可表示成 3 个点,如下图所示,以上代码就可产生图中的三条斜线。注意到,如在 x=2.0 处(绿色点)输出值很大时,及如在x=-1.0 处(紫色点)输出值很小时,斜线都非常十分平缓。如你所见,斜度最高的点位于 x=0 处(蓝色点)。这一特性非常重要。另外也可发现,所有的导数值都在 0 到 1 范围之内。
整体认识:误差项加权导数值
|
1
|
l1_delta
=
l1_error
*
nonlin
(
l1
,
True
)
|
当然,“误差项加权导数值”这个名词在数学上还有更为严谨的描述,不过我觉得这个定义准确地捕捉到了算法的意图。 l1_error 是一个(4,1)大小的矩阵,nonlin(l1,True)返回的便是一个(4,1)的矩阵。而我们所做的就是将其“逐元素地”相乘,得到的是一个(4,1)大小的矩阵 l1_delta ,它的每一个元素就是元素相乘的结果。
当我们将“斜率”乘上误差时,实际上就在以高确信度减小预测误差。回过头来看下 sigmoid 函数曲线图!当斜率非常平缓时(接近于 0),那么网络输出要么是一个很大的值,要么是一个很小的值。这就意味着网络十分确定是否是这种情况,或是另一种情况。然而,如果网络的判定结果对应(x = 0.5,y = 0.5)附近时,它便就不那么确定了。对于这种“似是而非”预测情形,我们对其做最大的调整,而对确定的情形则不多做处理,乘上一个接近于 0 的数,则对应的调整量便可忽略不计。
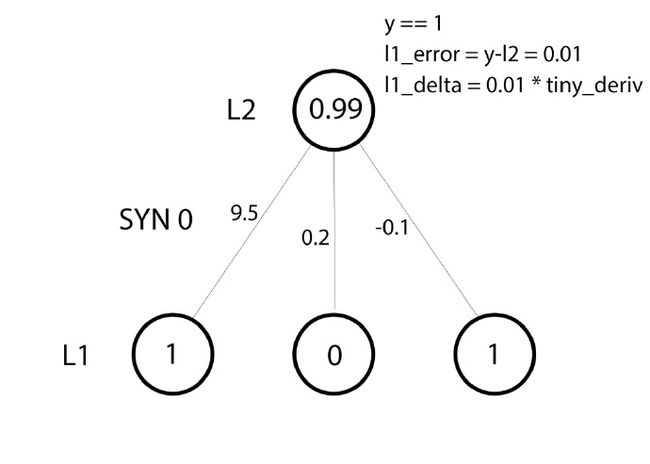
第 39 行:现在,更新网络已准备就绪!下面一起来看下一个简单的训练示例。
在这个训练示例中,我们已经为权值更新做好了一切准备。下面让我们来更新最左边的权值(9.5)。
权值更新量 = 输入值 * l1_delta
对于最左边的权值,在上式中便是 1.0 乘上 l1_delta 的值。可以想得到,这对权值 9.5 的增量是可以忽略不计的。为什么只有这么小的更新量呢?是因为我们对于预测结果十分确信,而且预测结果有很大把握是正确的。误差和斜率都偏小时,便意味着一个较小的更新量。考虑所有的连接权值,这三个权值的增量都是非常小的。
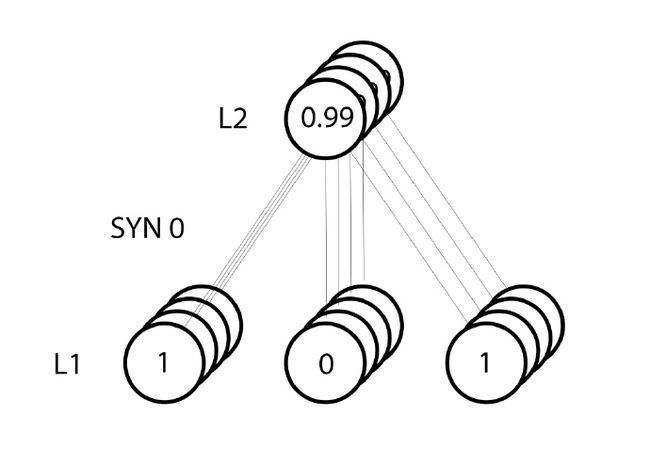
然而,由于采取的是“整批”训练的机制,因此上述更新步骤是在全部的 4 个训练实例上进行的,这看上去也有点类似于图像。那么,第 39 行做了什么事情呢?在这简单的一行代码中,它共完成了下面几个操作:首先计算每一个训练实例中每一个权值对应的权值更新量,再将每个权值的所有更新量累加起来,接着更新这些权值。亲自推导下这个矩阵相乘操作,你便能明白它是如何做到这一点的。
重点结论:
现在,我们已经知晓神经网络是如何进行更新的。回过头来看看训练数据,作一些深入思考。 当输入和输出均为 1 时,我们增加它们间的连接权重;当输入为 1 而输出为 0 时,我们减小其连接权重。
因此,在如下 4 个训练示例中,第一个输入结点与输出节点间的权值将持续增大或者保持不变,而其他两个权值在训练过程中表现为同时增大或者减小(忽略中间过程)。这种现象便使得网络能够基于输入与输出间的联系进行学习。
第二部分:一个稍显复杂的问题
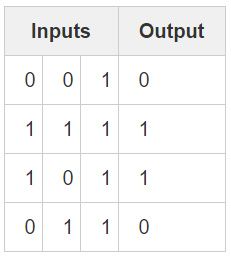
考虑如下情形:给定前两列输入,尝试去预测输出列。一个关键点在于这两列与输出不存在任何关联,每一列都有 50% 的几率预测结果为 1 ,也有 50% 的几率预测为 0 。
那么现在的输出模式会是怎样呢?看起来似乎与第三列毫不相关,其值始终为 1 。而第 1 列和第 2 列可以有更为清晰的认识,当其中 1 列值为1(但不同时为 1 !)时,输出便为 1 。这边是我们要找的模式!
以上可以视为一种“非线性”模式,因为单个输入与输出间不存在一个一对一的关系。而输入的组合与输出间存在着一对一的关系,在这里也就是列 1 和列 2 的组合。
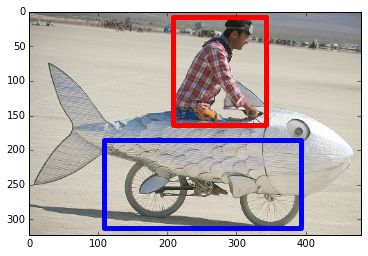
信不信由你,图像识别也是一种类似的问题。若有 100 张尺寸相同的烟斗图片和脚踏车图片,那么,不存在单个像素点位置能够直接说明某张图片是脚踏车还是烟斗。单纯从统计角度来看,这些像素可能也是随机分布的。然而,某些像素的组合却不是随机的,也就是说,正是这种组合才形成了一辆脚踏车或者是一个人。
我们的策略
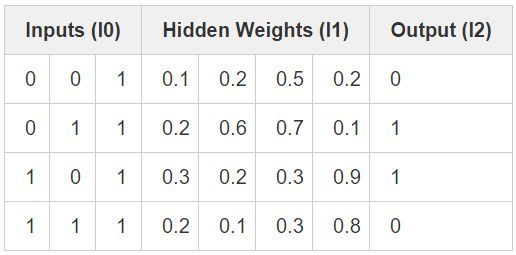
由上可知,像素组合后的产物与输出存在着一对一的关系。为了先完成这种组合,我们需要额外增加一个网络层。第一层对输入进行组合,然后以第一层的输出作为输入,通过第二层的映射得到最终的输出结果。在给出具体实现之前,我们来看下这张表格。
权重随机初始化好后,我们便得到了层1的隐态值。注意到什么了吗?第二列(第二个隐层结点)已经同输出有一定的相关度了!虽不是十分完美,但也可圈可点。无论你是否相信,寻找这种相关性在神经网络训练中占了很大比重。(甚至可以认定,这也是训练神经网络的唯一途径),随后的训练要做的便是将这种关联进一步增大。syn1 权值矩阵将隐层的组合输出映射到最终结果,而在更新 syn1 的同时,还需要更新 syn0 权值矩阵,以从输入数据中更好地产生这些组合。
注释:通过增加更多的中间层,以对更多关系的组合进行建模。这一策略正是广为人们所熟知的“深度学习”,因为其正是通过不断增加更深的网络层来建模的。
3 层神经网络:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
import
numpy
as
np
def
nonlin
(
x
,
deriv
=
False
)
:
if
(
deriv
==
True
)
:
return
x
*
(
1
-
x
)
return
1
/
(
1
+
np
.
exp
(
-
x
)
)
X
=
np
.
array
(
[
[
0
,
0
,
1
]
,
[
0
,
1
,
1
]
,
[
1
,
0
,
1
]
,
[
1
,
1
,
1
]
]
)
y
=
np
.
array
(
[
[
0
]
,
[
1
]
,
[
1
]
,
[
0
]
]
)
np
.
random
.
seed
(
1
)
# randomly initialize our weights with mean 0
syn0
=
2
*
np
.
random
.
random
(
(
3
,
4
)
)
-
1
syn1
=
2
*
np
.
random
.
random
(
(
4
,
1
)
)
-
1
for
j
in
xrange
(
60000
)
:
# Feed forward through layers 0, 1, and 2
l0
=
X
l1
=
nonlin
(
np
.
dot
(
l0
,
syn0
)
)
l2
=
nonlin
(
np
.
dot
(
l1
,
syn1
)
)
# how much did we miss the target value?
l2_error
=
y
-
l2
if
(
j
%
10000
)
==
0
:
print
"Error:"
+
str
(
np
.
mean
(
np
.
abs
(
l2_error
)
)
)
# in what direction is the target value?
# were we really sure? if so, don't change too much.
l2_delta
=
l2_error
*
nonlin
(
l2
,
deriv
=
True
)
# how much did each l1 value contribute to the l2 error (according to the weights)?
l1_error
=
l2_delta
.
dot
(
syn1
.
T
)
# in what direction is the target l1?
# were we really sure? if so, don't change too much.
l1_delta
=
l1_error
*
nonlin
(
l1
,
deriv
=
True
)
syn1
+=
l1
.
T
.
dot
(
l2_delta
)
syn0
+=
l0
.
T
.
dot
(
l1_delta
)
|
| 变量 | 定义说明 |
|---|---|
| X | 输入数据集,形式为矩阵,每 1 行代表 1 个训练样本。 |
| y | 输出数据集,形式为矩阵,每 1 行代表 1 个训练样本。 |
| l0 | 网络第 1 层,即网络输入层。 |
| l1 | 网络第 2 层,常称作隐藏层。 |
| l2 | 假定为网络最后一层,随着训练进行,其输出应该逐渐接近正确结果 |
| syn0 | 第一层权值,突触 0 ,连接 l0 层与 l1 层。 |
| syn1 | 第二层权值,突触 1 ,连接 l1 层与 l2 层。 |
| l2_error | 该值说明了神经网络预测时“丢失”的数目。 |
| l2_delta | 该值为经确信度加权后的神经网络的误差,除了确信误差很小时,它近似等于预测误差。 |
| l1_error | 该值为 l2_delta 经 syn1 加权后的结果,从而能够计算得到中间层/隐层的误差。 |
| l1_delta | 该值为经确信度加权后的神经网络 l1 层的误差,除了确信误差很小时,它近似等于 l1_error 。 |
一切看起来都如此熟悉!这只是用这样两个先前的实现相互堆叠而成的,第一层(l1)的输出就是第二层的输入。唯一所出现的新事物便是第 43 行代码。
第 43 行:通过对 l2 层的误差进行“置信度加权”,构建 l1 层相应的误差。为了做到这点,只要简单的通过 l2 与 l1 间的连接权值来传递误差。这种做法也可称作“贡献度加权误差”,因为我们学习的是,l1 层每一个结点的输出值对 l2 层节点误差的贡献程度有多大。接着,用之前 2 层神经网络实现中的相同步骤,对 syn0 权值矩阵进行更新。
第三部分:总结与展望
个人建议:
如果你想认真弄懂神经网络,给你一点建议:凭借记忆尝试去重构这个网络。我知道这听起来有一些疯狂,但确实会有帮助的。如果你想能基于新的学术文章创造任意结构的神经网络,或者读懂不同网络结构的样例程序,我觉得这项训练会是一个杀手锏。即使当你在使用一些开源框架时,比如 Torch ,Caffe 或者 Theano ,这也会有所帮助的。在执行这种练习之前,我接触神经网络有好几年了。而这段时间也是我在这一领域所作的做好的投资(也没有花费很长时间)。
工作展望
这个示例仍需附加一些其它功能,才能真正与业内最佳的网络结构相媲美。如果你想进一步改进你的网络,这里给出一些参考点。(后续可能还有更新)
学习速率
- 偏置单元
- 小批量
- Delta修剪
- 网络层大小参数化
- 正则化
- 概率输出
- 动量因子
- 批量归一化
- GPU兼容性
- 你自己的一些奇思妙想
想要从事机器学习方面的工作?
学习机器学习最好的途径,就是找一份相关的工作,这样你就能更专业地去实践机器学习。找工作时,建议你去查看下 Digital Reasoning 上面的职位,也尽管在我的 LinkedIn 上给我发消息。我很乐意倾听你对职业生涯的规划,也可以帮助你评估 Digital Reasoning 上的职位是否合适。
假如里面的职位你觉得都不太合适,继续找找看!机器学习,是如今职场中最有价值的一项技能。