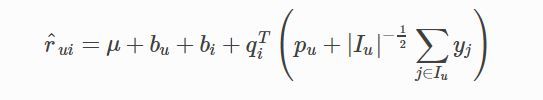python实现svd++推荐算法
之前写过用python实现svd推荐算法,这次更进一步,在原来的基础上实现了svd++算法,基本框架和之前一篇是类似的.
SVD++算法的预测评分式子如下。
与SVD相比增加的是这部分:
它的含义是这样的:评分行为从侧面反映了用户的喜好,可以将这样的反映通过隐式参数形式体系在模型中,得到的就是上式的部分,其中Iu是用户u评论过的物品的集合,yj为隐藏的评价了物品j的个人喜好偏置,也通过梯度下降算法优化。这里的-1/2是个经验值。
详细代码如下:
import numpy as np
import random
'''
author:huang
svd++ algorithm
'''
class SVDPP:
def __init__(self,mat,K=20):
self.mat=np.array(mat)
self.K=K
self.bi={}
self.bu={}
self.qi={}
self.pu={}
self.avg=np.mean(self.mat[:,2])
self.y={}
self.u_dict={}
for i in range(self.mat.shape[0]):
uid=self.mat[i,0]
iid=self.mat[i,1]
self.u_dict.setdefault(uid,[])
self.u_dict[uid].append(iid)
self.bi.setdefault(iid,0)
self.bu.setdefault(uid,0)
self.qi.setdefault(iid,np.random.random((self.K,1))/10*np.sqrt(self.K))
self.pu.setdefault(uid,np.random.random((self.K,1))/10*np.sqrt(self.K))
self.y.setdefault(iid,np.zeros((self.K,1))+.1)
def predict(self,uid,iid): #预测评分的函数
#setdefault的作用是当该用户或者物品未出现过时,新建它的bi,bu,qi,pu及用户评价过的物品u_dict,并设置初始值为0
self.bi.setdefault(iid,0)
self.bu.setdefault(uid,0)
self.qi.setdefault(iid,np.zeros((self.K,1)))
self.pu.setdefault(uid,np.zeros((self.K,1)))
self.y.setdefault(uid,np.zeros((self.K,1)))
self.u_dict.setdefault(uid,[])
u_impl_prf,sqrt_Nu=self.getY(uid, iid)
rating=self.avg+self.bi[iid]+self.bu[uid]+np.sum(self.qi[iid]*(self.pu[uid]+u_impl_prf)) #预测评分公式
#由于评分范围在1到5,所以当分数大于5或小于1时,返回5,1.
if rating>5:
rating=5
if rating<1:
rating=1
return rating
#计算sqrt_Nu和∑yj
def getY(self,uid,iid):
Nu=self.u_dict[uid]
I_Nu=len(Nu)
sqrt_Nu=np.sqrt(I_Nu)
y_u=np.zeros((self.K,1))
if I_Nu==0:
u_impl_prf=y_u
else:
for i in Nu:
y_u+=self.y[i]
u_impl_prf = y_u / sqrt_Nu
return u_impl_prf,sqrt_Nu
def train(self,steps=30,gamma=0.04,Lambda=0.15): #训练函数,step为迭代次数。
print('train data size',self.mat.shape)
for step in range(steps):
print('step',step+1,'is running')
KK=np.random.permutation(self.mat.shape[0]) #随机梯度下降算法,kk为对矩阵进行随机洗牌
rmse=0.0
for i in range(self.mat.shape[0]):
j=KK[i]
uid=self.mat[j,0]
iid=self.mat[j,1]
rating=self.mat[j,2]
predict=self.predict(uid, iid)
u_impl_prf,sqrt_Nu=self.getY(uid, iid)
eui=rating-predict
rmse+=eui**2
self.bu[uid]+=gamma*(eui-Lambda*self.bu[uid])
self.bi[iid]+=gamma*(eui-Lambda*self.bi[iid])
self.pu[uid]+=gamma*(eui*self.qi[iid]-Lambda*self.pu[uid])
self.qi[iid]+=gamma*(eui*(self.pu[uid]+u_impl_prf)-Lambda*self.qi[iid])
for j in self.u_dict[uid]:
self.y[j]+=gamma*(eui*self.qi[j]/sqrt_Nu-Lambda*self.y[j])
gamma=0.93*gamma
print('rmse is',np.sqrt(rmse/self.mat.shape[0]))
def test(self,test_data): #gamma以0.93的学习率递减
test_data=np.array(test_data)
print('test data size',test_data.shape)
rmse=0.0
for i in range(test_data.shape[0]):
uid=test_data[i,0]
iid=test_data[i,1]
rating=test_data[i,2]
eui=rating-self.predict(uid, iid)
rmse+=eui**2
print('rmse of test data is',np.sqrt(rmse/test_data.shape[0]))
def getMLData(): #获取训练集和测试集的函数
import re
f=open("C:/Users/xuwei/Downloads/ml-100k/ml-100k/u1.base",'r')
lines=f.readlines()
f.close()
data=[]
for line in lines:
list=re.split('\t|\n',line)
if int(list[2]) !=0:
data.append([int(i) for i in list[:3]])
train_data=data
f=open("C:/Users/xuwei/Downloads/ml-100k/ml-100k/u1.test",'r')
lines=f.readlines()
f.close()
data=[]
for line in lines:
list=re.split('\t|\n',line)
if int(list[2]) !=0:
data.append([int(i) for i in list[:3]])
test_data=data
return train_data,test_data
train_data,test_data=getMLData()
a=SVDPP(train_data,30)
a.train()
a.test(test_data)