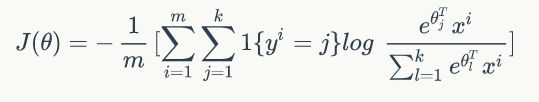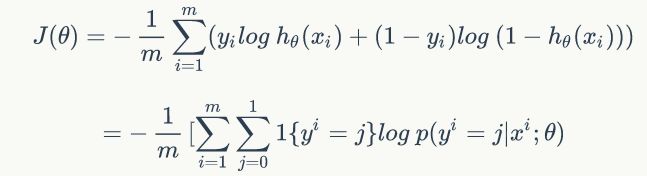深入理解机器学习中的各种熵和信息：信息量，熵，交叉熵，相对熵，条件熵，互信息等。

对机器学习了解的读者肯定经常听到以下名词：信息量，熵，交叉熵，相对熵，条件熵，互信息等。很多人对这些大同小异的名词很容易产生迷惑，它们之间究竟有什么关系？

本篇博客在参考文献的基础上，从我自己理解的角度上，依次介绍信息量、信息熵、交叉熵、相对熵、条件熵、互信息、信息增益和信息增益率，试图清晰地说明这些概念之间的区别和联系。有些概念为了生动，我会举例说明，有些概念为了严谨，我会从公式推导上说明。

一、信息量

信息量是理解其它概念的基础。

信息量是对信息的度量，就跟时间的度量是秒一样，以离散的随机变量$X$为例，当我们观察到的这个变量的一个具体值的时候，我们接收到了多少信息呢？多少信息就用信息量来衡量，我们接受到的信息量跟具体发生的事件有关。

信息量的大小可以衡量事件的不确定性或发生的惊讶程度。一个事件发生的概率越小则其所含的信息量越大。比如说太阳从东方升起，这个事情是一定发生的，那么这句话的信息量就很少。又比如，在夏天，天气预报说，明天气温小于零摄氏度，我们知道，发生这样的事情概率很低，那就说明这件事信息量很大。因此一个具体事件的信息量应该是随着其发生概率而递减的，且不能为负。

我们形式化地写明信息量，设事件发生的概率为$p(x)$，则其信息量表示为
$$h(x)=-{\mathrm{l}\mathrm{o}\mathrm{g}}_{2}p(x)\text{(1)}$$

写成对数形式有一个好处：如果我们有两个不相关的事件$X$和$Y$，那么我们观察到的这两个事件同时发生时获得的信息应该等于观察到的事件各自发生时获得的信息之和，即：$h(x,y)=h(x)+h(y)$。而对于不相关事件的概率，有$p(x,y)=p(x)\ast p(y)$。因此，写成对数形式可以满足这种关系。即
$$h(x,y)=-{\mathrm{l}\mathrm{o}\mathrm{g}}_{2}p(x,y)=-{\mathrm{l}\mathrm{o}\mathrm{g}}_2(p(x)\ast p(y))=-{\mathrm{l}\mathrm{o}\mathrm{g}}_{2}p(x)-{\mathrm{l}\mathrm{o}\mathrm{g}}_{2}p(y)=h(x)+h(y)$$

对公式（1）还要说明2点：

• 负号是为了确保信息一定是正数或者是0

• 底数为2只是遵循信息论的普遍传统，原则上，对数的底数使用多少都可以

二、信息熵

说明了信息量，我们来说信息熵。信息熵又称为熵。

对于一个随机变量$X$而言，它的所有可能取值的信息量的期望就称为信息熵。

对于离散变量来说，信息熵为
$$H(x)=-\sum _{x\in X}p(x)\mathrm{l}\mathrm{o}\mathrm{g}p(x)\text{(2)}$$

对于连续变量来说，信息熵为
$$H(x)=-{\int }_{x\in X}p(x)\mathrm{l}\mathrm{o}\mathrm{g}p(x)dx\text{(3)}$$

从信息熵的公式我们可以得到：如果随机变量的取值越多，那么它的信息熵越大。如果取值越均匀，信息熵越大。

如图，考虑只有两种结果的随机变量，横轴为其中一个结果的概率，当2种结果概率为0.5时，信息熵达到最大,当2种结果有1种结果为0或者1时，即左右两端时，信息熵为零。

三、交叉熵

在《深度学习（二）：DNN损失函数和激活函数的选择》中，我们曾经使用过交叉熵损失函数。在这里，我们介绍下交叉熵的概念。

现在有样本集的两种概率分布$p$和$q$，其中$p$是样本的真实分布，$q$为非真实分布（可以看做是预测分布）。在训练过程中，我们学习到了非真实分布$q$，则是基于分布$q$的信息量的期望，但是由于样本来自于分布$p$，因此期望与真实分布一致，所以基于$q$的样本预测公式为：
$$CEH(p,q)=-\sum _{x\in X}p(x)\mathrm{l}\mathrm{o}\mathrm{g}q(x)\text{(4)}$$

在信息论中，其计算的数值表示：如果用错误的编码方式$q$去编码真实分布$p$的事件，需要多少bit数，是一种非常有用的衡量概率分布相似性的数学工具。

在我们熟悉的逻辑回归中，其损失函数就是交叉熵，也叫做负对数似然。这里引用参考文献【1】：

对于多分类的逻辑回归算法，通常我们使用Softmax作为输出层映射，其对应的损失函数也叫交叉熵，只不过写法有点区别，具体如下：

其中，$m$是样本个数,$k$是输出层个数。

可以看出，其实两者是一样的，softmax只是对sigmoid在多分类上面的推广。

四、相对熵

相对熵与交叉熵的关系较为密切。相对熵又称为KL散度，是度量用非真实分布$q$预测样本与用真实分布$p$预测样本的差值。
$$\begin{array}{rl}KL(p,q)& =CEH(p,q)-H(p)\\ & =-\sum _{k=1}^N{p}_k\mathrm{l}\mathrm{o}\mathrm{g}{q}_k-(-\sum _{k=1}^N{p}_k\mathrm{l}\mathrm{o}\mathrm{g}{p}_k)\\ & =\sum _{k=1}^N{p}_k\mathrm{l}\mathrm{o}\mathrm{g}\frac{1}{q_k}-\sum _{k=1}^N{p}_k\mathrm{l}\mathrm{o}\mathrm{g}\frac{1}{p_k}\\ & =\sum _{k=1}^N{p}_k\mathrm{l}\mathrm{o}\mathrm{g}\frac{p_k}{q_k}\end{array}\text{(5)}$$

机器学习的目的就是使$q(x)$更加接近$p(x)$，因此我们自然而然想到就是要求相对熵的最小值。而相对熵公式中的后一项由于$p(x)$的分布是确定的，因此可以说是常数，这样就变成了求交叉熵的最小值。这就是为什么要最小化交叉熵损失函数的原因。

五、条件熵

根据第二章，我们已经知道信息熵为随机变量所有可能取值的信息量的期望。

对于离散变量来说，信息熵为
$$H(x)=-\sum _{x\in X}p(x)\mathrm{l}\mathrm{o}\mathrm{g}p(x)\text{(2)}$$

而条件熵$H(Y|X)$定义为在$X$给定条件下，$Y$的条件概率分布的熵对$X$的数学期望。
条件熵形式化如下：
$$\begin{array}{rl}H(Y|X)& =-\sum _{x\in X}p(x)H(Y|X=x)\\ & =-\sum _{x\in X}p(x)\sum _{y\in Y}p(y|x)\mathrm{l}\mathrm{o}\mathrm{g}p(y|x)\\ & =-\sum _{x\in X}\sum _{y\in Y}p(x,y)\mathrm{l}\mathrm{o}\mathrm{g}p(y|x)\end{array}\text{(6)}$$

注：条件熵中$X$也是一个变量，意思是在一个变量$X$的条件下（变量$X$的每个值都会取），另一个变量$Y$熵对$X$的期望。并非：在给定某个数（某个变量为某个值）的情况下，另一个变量的熵是多少。

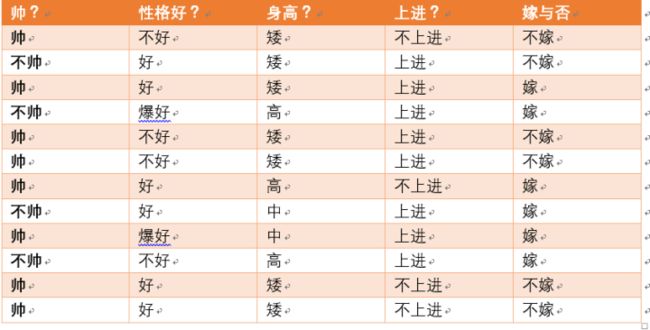
我们这里引用参考文献【3】中的例子，来形象地解释上面的话：

假如我们有上面数据：设随机变量$Y=嫁，不嫁$。我们可以统计出，嫁的个数为6/12 = 1/2，不嫁的个数为6/12 = 1/2，那么$Y$的熵，根据熵的公式来算，可以得到$H(Y)=-1/2log1/2-1/2log1/2=1$

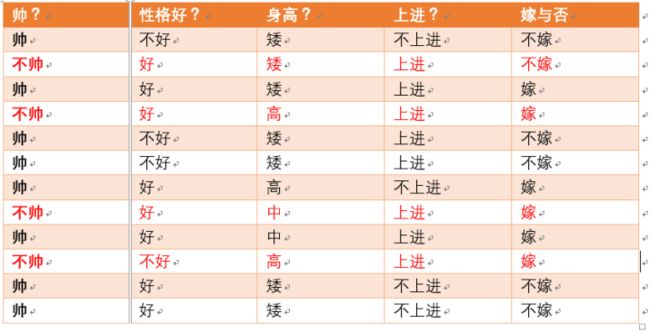
为了引出条件熵，我们现在还有一个变量$X$，代表长相是帅还是帅，当长相是不帅的时候，统计如下红色所示：

可以得出，当已知不帅的条件下，满足条件的只有4个数据了，即$p(X=不帅)=4/12=1/3$。

这四个数据中，不嫁的个数为1个，占1/4，嫁的个数为3个，占3/4。那么此时的$H(Y|X=不帅)=-1/4log1/4-3/4log3/4=0.81$

同理我们可以得到：当已知帅的条件下，满足条件的有8个数据，即$p(X=帅)=8/12=2/3$。

这八个数据中，不嫁的个数为5个，占5/8，嫁的个数为3个，占3/8。那么此时的$H(Y|X=帅)$ = $-5/8log5/8-3/8log3/8=0.95$

有了上面的铺垫之后，现在可以计算条件熵了，即求：$H(Y|X=长相)$。也就是说，我们想要求出当已知长相的条件下的条件熵。

我们已经知道条件熵是另一个变量Y熵对X（条件）的期望。且长相可以取帅与不帅两种，根据公式（6），有

$$\begin{array}{rl}H(Y|X=长相)& =p(X=帅)\ast H(Y|X=帅)+p(X=不帅)\ast H(Y|X=不帅)\\ & =0.667\ast 0.95+0.333\ast 0.81\\ & =0.903\end{array}$$

总结一下，其实条件熵意思是按一个新的变量的每个值对原变量进行分类，比如上面这个题把嫁与不嫁按帅，不帅分成了两类。然后在每一个小类里面，都计算一个小熵，然后每一个小熵乘以各个类别的概率，然后求和。

其实，简单来说，$H(Y|X)$就是已经$X$的情况下，$Y$的不确定度（熵）。

六、互信息

互信息的定义为：一个随机变量由于已知另一个随机变量而减少的不确定性。或者说，有两个随机变量，引入一个，能给另外一个带来多少信息。

互信息的公式如下：
$$I(X,Y)=H(Y)-H(Y|X)\text{(7)}$$

其中，$H(Y)$是$Y$的熵，$H(Y|X)$是条件熵。

上面的介绍大家应该很面熟，因为我们在第五章条件熵中的例子已经体现出了这一点。

在第五章中，我们用另一个变量长相$X$对原变量嫁不嫁$Y$分类后，原变量$Y$的不确定性就会减小了，因为新增了$X$的信息。不确定程度减少了多少就是信息的增益。在上面的例子中，在没有$X$的情况下，$H(Y)=1$，在有了$X$的情况下，$H(Y|X)=0.903$。因此$I(X,Y)=1-0.903=0.097$，即把$X$引入后，$Y$的不确定减少了0.097.

针对公式（7），我们可以看到：

• 当$X$与$Y$独立时，$X$并没有给$Y$带来任何信息，$H(Y|X)=H(Y)$，故$I(X,Y)=0$

• 当$X$与$Y$完全相关时，即已知$X$，就完全知道了$Y$，$H(Y|X)=0$，故$I(X,Y)=H(Y)$

• $X$与$Y$关系越密切，$I(X,Y)$就越大。

七、信息增益

信息增益是决策树ID3算法在进行特征选择时使用的划分准则，其公式与互信息完全相同。其公式如下：
$$G(D,A)=H(D)-H(D|A)\text{(8)}$$

其中，$D$表示数据集，$A$表示特征，信息增益表示得到$A$的信息而使得类$X$的不确定度下降的程度，在ID3中，需要选择一个$A$使得信息增益最大，这样可以使得分类系统进行快速决策。

需要注意的是：在数值上，信息增益和互信息完全相同，但意义不一样，需要区分，当我们说互信息时候，两个随机变量的地位是相同的，可以认为是纯数学工具，不考虑物理意义，当我们说信息增益时候，是把一个变量看成是减少另一个变量不确定度的手段。

八、信息增益率

信息增益率是决策树C4.5算法引入的划分特征准则，其主要是克服信息增益存在的在某种特征上分类特征太细，但实际上无意义取值时候导致的决策树划分特征失误的问题。例如假设有一列特征是身份证ID，每个人的都不一样，其信息增益肯定是最大的，但是对于一个情感分类系统来说，这个特征是没有意义的，此时如果采用ID3算法就会出现失误，而C4.5正好克服了该问题。其公式如下：
$$G_r(D,A)=\frac{G(D,A)}{H(A)}\text{(9)}$$

参考文献

【1】深度学习理论——信息量，信息熵，交叉熵，相对熵及其在机器学习中的应用

【2】通俗理解信息熵

【3】通俗理解条件熵

【4】机器学习各种熵：从入门到全面掌握

【5】【周末AI课堂】深度学习中的熵（理论篇）| 机器学习你会遇到的“坑”